High-precision decoupling calibration method of multi-dimensional mounting spacecraft
-
摘要:
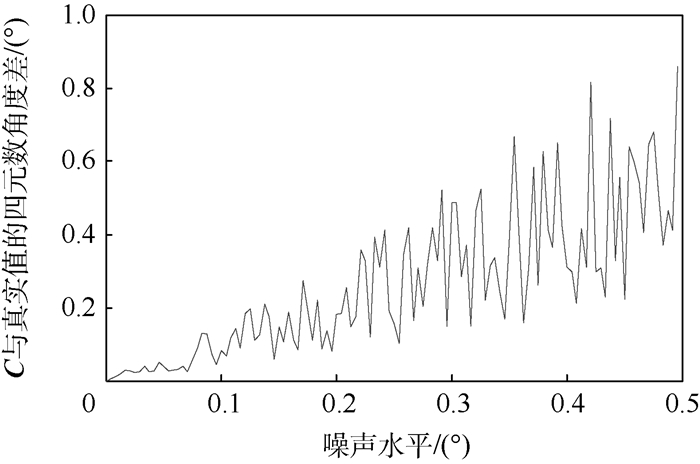
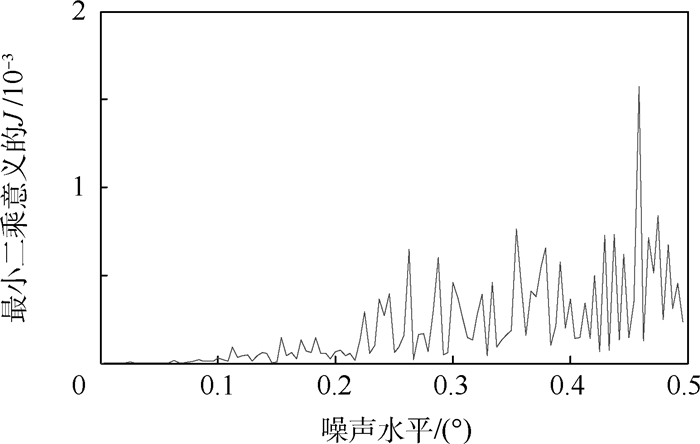
针对航天器多维安装在耦合情形下的标定问题，提出一种基于成像器观测的在轨标定方法，该方法有效克服了标定方程组的耦合非线性。首先，结合成像器观测的物理意义推导出其应满足的几何方程，并通过各机械机构的安装传递关系建立矢量方程，进而通过双矢量方式建立矩阵方程。其次，分析矩阵方程成立应当满足的必要条件，通过灵活运用"特征向量"的数学特性，对串联机械机构安装进行解耦，得出一种以成像器观测为基础的在轨标定数学方法，并将2维安装推广到n维安装的一般情形，给出标准的计算流程。最后，对标定方法进行了数学仿真验证，同时仿真分析了观测噪声对标定方法的影响，仿真结果表明灵活运用"特征向量"解耦标定的方法是有效的、准确的。
Abstract:Aimed at the calibration problem of spacecraft multi-dimensional installation in the coupling situation, an on-orbit calibration method based on imager observation is proposed, and this method effectively overcomes the coupling nonlinearity of the calibration equations. Firstly, the geometric equations that should be satisfied are derived by combining the physical meanings of the imager observation, the vector equations are established by the installation and transfer relationship of each mechanical mechanism, and then the matrix equations are established by the dual-vector method. Secondly, the necessary conditions for the establishment of the matrix equation are analyzed. Through flexible use of the mathematical characteristics of "eigenvector", the installation of the series mechanical mechanism is decoupled, and a mathematical method for on-orbit calibration based on imager observation is obtained, extending the two-dimensional installation to the general case of n-dimensional installation, and giving a standard calculation process. Finally, the calibration algorithm is verified by mathematical simulation. At the same time, the influence of observation noise on the calibration method is simulated. The simulation results show that the method of decoupling calibration using "eigenvector" is effective and accurate.
-
Key words:
- spacecraft /
- installation errors /
- on-orbit calibration /
- multi-dimension /
- eigenvector
-
图 4 A的标定误差随观测噪声变化
Figure 4. Variation of calibration error of A with observation noise
图 5 C的标定误差随观测噪声变化
Figure 5. Variation of calibration error of C with observation noise
图 6 J的标定误差随观测噪声变化
Figure 6. Variation of calibration error of J with observation noise
表 1 恒星方位数据(J2000系下单位矢量)
Table 1. Stellar orientation data (unit vector in J2000 coordinate system)
坐标 第1次 第2次 第3次 第4次 第5次 第6次 x 0.775 810 6 0.416 382 6 -0.440 612 21 -0.946 873 74 -0.384 996 277 0 0.372 642 24 y 0.602 428 5 0.170 308 8 -0.728 514 67 -0.174 203 86 0.768 706 644 40 0.885 212 69 z 0.187 610 4 0.893 095 9 0.524 525 74 -0.270 338 9 -0.510 752 348 5 -0.278 453 29 
下载: 导出CSV
表 2 星点方位数据(观测器系下单位矢量)
Table 2. Star orientation data (unit vector in observer coordinate system)
坐标 第1次 第2次 第3次 第4次 第5次 第6次 x 0.984 807 75 0.766 044 443 0.5 0.939 692 62 0.642 787 60 0.866 025 4 y 0.172 987 39 0.604 022 77 0.75 0.336 824 1 0.694 272 044 0.482 962 91 z 0.015 134 43 0.219 846 31 0.433 012 70 0.059 391 174 0.323 744 370 0.129 409 52
下载: 导出CSV
-
[1] LIKINS P W. Spacecraft attitude dynamics and control-a personal perspective on early developments[J].Journal of Guidance, Control, and Dynamics, 1986, 9(2):129-134. http://cn.bing.com/academic/profile?id=91cc5be5385c4e3340c62cee5ef34a75&encoded=0&v=paper_preview&mkt=zh-cn [2] 李青.充液挠性系统动力学分析及在航天工程中的应用研究[D].北京: 清华大学, 2010: 50-75.LI Q.Dynamic analysis of liquid-filled flexible systems and its application studies on aerospace engineering[D].Beijing: Tsinghua University, 2010: 50-75(in Chinese). [3] ZOU A M, KUMAR K D.Adaptive attitude control of spacecraft without velocity measurements using Chebyshev neural network[J].Acta Astronautica, 2010, 66(5-6):769-779. doi: 10.1016/j.actaastro.2009.08.020 [4] PECHEV C, ALEXANDRE N.Feedback-based steering law for control moment gyros[J].Journal of Guidance, Control, and Dynamics, 2007, 30(3):848-855. doi: 10.2514/1.27351 [5] ARDUINI C, BAIOCCO P.Active magnetic damping attitude control for gravity gradient stabilized spacecraft[J].Journal of Guidance, Control, and Dynamics, 1997, 20(1):117-122. [6] 周军.航天器控制原理[M].西安:西北工业大学出版社, 2000:62-68.ZHOU J.Principle of spacecraft control[M].Xi'an:Press of Northwestern Polytechnical University, 2000:62-68(in Chinese). [7] 黄圳圭.航天器姿态动力学[M].长沙:国防科技大学出版社, 1997:7-23.HUANG Z G.Spacecraft attitude dynamics[M].Changsha:Press of National University of Defense Technology, 1997:7-23(in Chinese). [8] 刘俊, 石云波, 李杰.微惯性技术[M].北京:电子工业出版社, 2005:15-33.LIU J, SHI Y B, LI J.Micro inertia technology[M].Beijing:Publishing House of Electronics Industry, 2005:15-33(in Chinese). [9] ZHU R, ZHOU Z Y.Calibration of three-dimensional intergrated sensors for improved system accuracy[J].Sensors and Actuators, 2006, 127:340-344. doi: 10.1016/j.sna.2005.12.001 [10] 刘秉, 闫建国.一种小型惯性测量单元的精确标定技术[J].计算机测量与控制, 2009, 17(11):2170-2172. http://d.old.wanfangdata.com.cn/Periodical/jsjzdclykz200911022LIU B, YAN J G.Precision-calibration technique for inertial measurement units[J].Computer Measurement and Control, 2009, 17(11):2170-2172(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jsjzdclykz200911022 [11] SHUSTER M D, OH S D.Three-axis attitude determination from vector observations[J].Journal of Guidance, Control, and Dynamics, 1981, 4(1):70-77. http://cn.bing.com/academic/profile?id=c1f9fe8db26cea8a0636e3312c8ff40d&encoded=0&v=paper_preview&mkt=zh-cn [12] MARKLEY F L, MORTARI D.Quaternion attitude estimation using vector observations[J].Journal of the Astronautical Sciences, 2000, 48(2):359-380. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ026104557/ [13] LERNER G M.Three-axis attitude determination[J].Spacecraft Attitude Determination and Control, 1978, 73:420-428. http://d.old.wanfangdata.com.cn/Periodical/gfkjdxxb200105005 [14] RENATO B, FABIO C.A robust optimization approach for magnetic spacecraft attitude stabilization[J].Journal of Optimization Theory and Applications, 2017, 173(3):994-1012. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=757e97ad51bcd874882efacf9c947869 [15] CHAK Y C, VARATHARAJOO R, RAZOUMNY Y.Disturbance observer-based fuzzy control for flexible spacecraft combined attitude & sun tracking system[J].Acta Astronautica, 2017, 133:302-310. doi: 10.1016/j.actaastro.2016.12.028 [16] STEVENSON D, SCHAUB H.Electrostatic spacecraft rate and attitude control-experimental results and performance considerations[J].Acta Astronautica, 2016, 119:22-33. doi: 10.1016/j.actaastro.2015.10.023 -
下载:
点击查看大图
计量
- 文章访问数: 678
- HTML全文浏览量: 197
- PDF下载量: 242
- 被引次数: 0
