-
摘要:
在推进剂贮箱服役期内，由于材料强度退化及外界随机载荷等不确定因素的存在，其可靠性表现为时变特性。基于区间理论与应力-强度干涉理论，为推进剂贮箱时变可靠性分析提供了一种区间干涉时变可靠性分析方法。通过对椭球底圆柱贮箱应力进行分析，根据贮箱等效应力分布与强度幂指数退化模型，将应力与强度转换为时变区间变量的形式。结合应力-强度干涉理论，将任意时刻应力与强度区间转换为标准化区间，根据临界状态函数与标准化区间的位置关系，定义区间干涉时变可靠性指标。结合示例参数对推进剂贮箱时变可靠性进行了分析，并与服从正态分布的应力-强度干涉可靠性方法及区间可靠性方法分析结果进行了对比，验证了所提方法的有效性。
Abstract:During the service period of propellant tank, due to the existence of uncertain factors such as structural strength degradation and external random loads, the reliability of propellant tank is with time-variant characteristic. Based on interval theory and stress-strength interference theory, an interval interference time-variant reliability analysis method is proposed for the time-variant reliability analysis of propellant tank. By analyzing the stress of the cylindrical tank with ellipsoid bottom, the stress and strength are converted into the form of time-varying interval variables according to the equivalent stress distribution and strength power exponential degradation model. Combined with the stress-strength interference theory, the stress and strength intervals at any time are converted into the standardized interval. According to the position relation between the critical state function and the standardized interval, the interval interference time-variant reliability index is defined. Finally, the time-variant reliability of tank is analyzed with the sample parameters, and the validity of the proposed method is verified by comparing with the stress-strength interference reliability that obeys normal distribution and the interval reliability analysis results.
-
图 4 贮箱椭球下底、圆柱筒和椭球上底可靠性指标
Figure 4. Reliability indexes of ellipsoid roof, cylinder and ellipsoid bottom
表 1 贮箱示例参数
Table 1. Sample parameters of tank
参数 数值 m 2 ρ/(kg·m-3) 1 000 P/MPa 0.1 Z/t 280 h/m 10.5 T/h 50 000 γ 4 a/m 2 hc/m 10 δc, δb/mm 4 δr/mm 3 Rr(X, 0)/MPa 30 Rc(X, 0)/MPa 300 R(X, T)/MPa 200 
下载: 导出CSV
表 2 贮箱应力区间参数
Table 2. Parameters of tank stress interval MPa
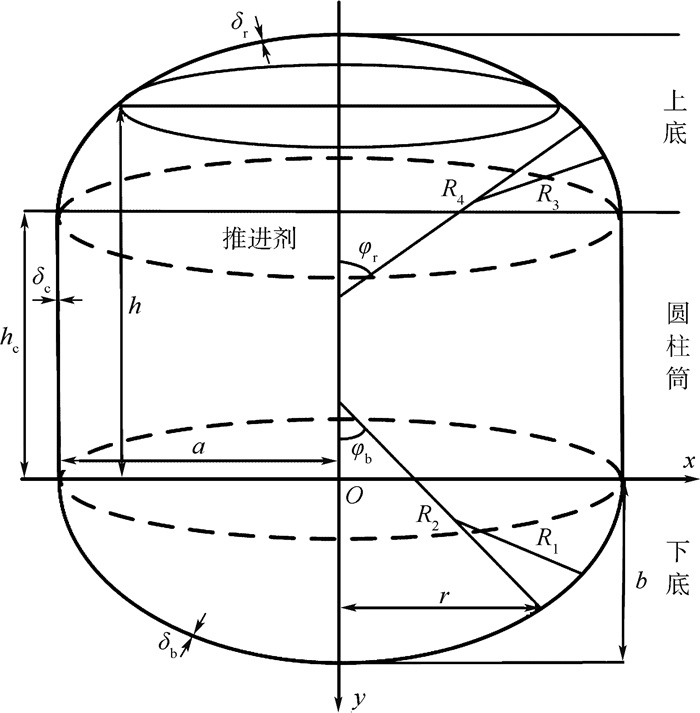
贮箱 
Sc(Y, t) Sr(Y, t) 上底 104.89 47.15 30 0 91.02 43.87 圆柱筒 131.10 82.07 30 0 121.59 39.52 下底 160.36 75.03 30 0 132.70 57.67
下载: 导出CSV
-
[1] SUDRET B.Analytical derivation of the outcrossing rate in time-variant reliability problems[J].Structure and Infrastructure Engineering, 2008, 4(5):353-362. doi: 10.1080/15732470701270058 [2] JIANG C, HUANG X P, WEI X P, et al.A time-variant reliability analysis method for structural systems based on stochastic process discretization[J].International Journal of Mechanics and Materials in Design, 2017, 13(2):173-193. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=995ad6ae9c87c11c0904ba7ff67ca4c9 [3] ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M.The PHI2 method:A way to compute time-variant reliability[J].Reliability Engineering & System Safety, 2004, 84(1):75-86. [4] SHI Y, LV Z Z.Dynamic reliability analysis model for structure with both random and interval uncertainties[J].International Journal of Mechanics and Materials in Design, 2018, 15(3):521-537. [5] PENG Y Z, YU W, ZI Y Y, et al.Dynamic reliability assessment and prediction for repairable systems with interval-censored data[J].Reliability Engineering & System Safety, 2017, 159:301-309. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d52ed3005b1315b3b4e952b6cea3c315 [6] WANG Z Q, CHEN W.Time-variant reliability assessment through equivalent stochastic process transformation[J].Reliability Engineering & System Safety, 2016, 152:166-175. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=2d98b7254a45796433bfef4bb8d991fa [7] YANG D Y, TENG J G, FRANGOPOL D M.Cross-entropy-based adaptive importance sampling for time-dependent reliability analysis of deterioration structures[J].Structural Safety, 2017, 66:38-50. doi: 10.1016/j.strusafe.2016.12.006 [8] ZHANG X Q, GAO H Y, HUANG H Z, et al.Dynamic reliability modeling for system analysis under complex load[J].Reliability Engineering & System Safety, 2018, 180:345-351. [9] XIA B Z, WNAG L F.Non-probabilistic interval process analysis of time-varying uncertain structures[J].Engineering Structures, 2018, 175:101-112. doi: 10.1016/j.engstruct.2018.07.098 [10] BEN-HAIM H Y.A non-probabilistic measure of reliability of linear systems based on expansion of convex models[J].Structural Safety, 1995, 17(2):91-109. http://cn.bing.com/academic/profile?id=d81f3a4704b00b944e3a2861c74cc7ef&encoded=0&v=paper_preview&mkt=zh-cn [11] ELISHAKOFF I.Discussion on:A non-probabilistic concept of reliability[J].Structural Safety, 1995, 17(3):195-199. doi: 10.1016/0167-4730(95)00010-2 [12] GUO S X, LV Z Z.Interval arithmetic and static interval finite element method[J].Applied Mathematics & Mechanics, 2001, 22(12):1390-1396. http://cn.bing.com/academic/profile?id=247ffdc657e5d1f350995150a34f5085&encoded=0&v=paper_preview&mkt=zh-cn [13] QIU Z P, WANG X J.Comparison of dynamic response of structures with uncertain-but-bounded parameters using non-probabilistic interval analysis method and probabilistic approach[J].International Journal of Solids & Structures, 2003, 40(20):5423-5439. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=459ec8cb6f949512e66d4225155e0176 [14] WANG X J, WANG R X, WANG L, et al.An efficient single-loop strategy for reliability-based multidisciplinary design optimization under non-probabilistic set theory[J].Aerospace Science & Technology, 2017, 73:148-163. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c690974d7d7ebb38841083cc72690cde [15] NI B Y, JIANG C, HUANG Z L.Discussions on non-probabilistic convex modelling for uncertain problems[J].Applied Mathematical Modelling, 2018, 59:54-85. doi: 10.1016/j.apm.2018.01.026 [16] 王心清.结构设计[M].2版.北京:中国宇航出版社, 2009:19-35.WANG X Q.The structural design[M].2nd ed.Beijing:China Astronautic Publishing House, 2009:19-35(in Chinese). [17] SCHAFF J R, DAVIDSON B D.Life prediction methodology for composite structures.Part I-Constant amplitude and two-stress level fatigue[J].Journal of Composite Materials, 1997, 31(2):158-181. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/002199839703100202 [18] AN Z W, HUANG H Z, LIU Y.A discrete stress-strength interference model based on universal generating function[J].Reliability Engineering & System Safety, 2008, 93(10):1485-1490. http://cn.bing.com/academic/profile?id=3e5461619ad2c14db549940ad207e7ff&encoded=0&v=paper_preview&mkt=zh-cn [19] SU H Z, LI J Y, WEN Z P, et al.Dynamic non-probabilistic reliability evaluation and service life prediction for arch dams considering time-varying effects[J].Applied Mathematical Modelling, 2016, 40(16):6908-6923. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bc0f12eb71eab43d3d0be01c76a4a96e -
下载:
点击查看大图
计量
- 文章访问数: 694
- HTML全文浏览量: 153
- PDF下载量: 152
- 被引次数: 0
