一种飞机大尺寸曲面测量点差异性规划方法

毛喆; 李泷杲; 徐岩; 曾琪; 主逵

doi:10.13700/j.bh.1001-5965.2019.0334

一种飞机大尺寸曲面测量点差异性规划方法

doi: 10.13700/j.bh.1001-5965.2019.0334

毛喆¹,
李泷杲^1, ,,
徐岩¹,
曾琪¹,
主逵²

1.
南京航空航天大学机电学院, 南京 210016
2.
深圳市劲拓自动化设备股份有限公司, 深圳 518101

基金项目:

国家重点研发计划 2017YFF0107304

详细信息

作者简介:
毛喆  男, 硕士研究生。主要研究方向:飞机数字化装配与测量

李泷杲  男, 博士, 副教授, 硕士生导师。主要研究方向:飞机数字化装配与测量

徐岩  男, 博士, 副教授, 硕士生导师。主要研究方向:制造业信息化、CAD/CAM技术

通讯作者:
李泷杲, E-mail:lishuanggao@nuaa.edu.cn

中图分类号: V241.05;TP391
计量
- 文章访问数: 636
- HTML全文浏览量: 79
- PDF下载量: 114
- 被引次数: 0
出版历程
- 收稿日期: 2019-06-25
- 录用日期: 2019-09-27
- 网络出版日期: 2020-05-20

A difference measurement points planning method for large-scale surface of aircraft

MAO Zhe¹,
LI Shuanggao^{1
, ,},
XU Yan¹,
ZENG Qi¹,
ZHU Kui²

1.
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
2.
Shenzhen JT Automation Equipment Co. Ltd., Shenzhen 518101, China

Funds:

National Key R & D Program of China 2017YFF0107304

More Information

Corresponding author: LI Shuanggao, E-mail:lishuanggao@nuaa.edu.cn

摘要

摘要:
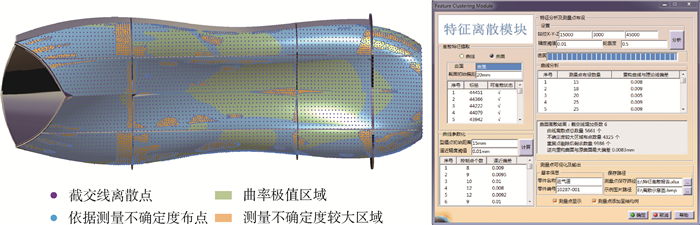
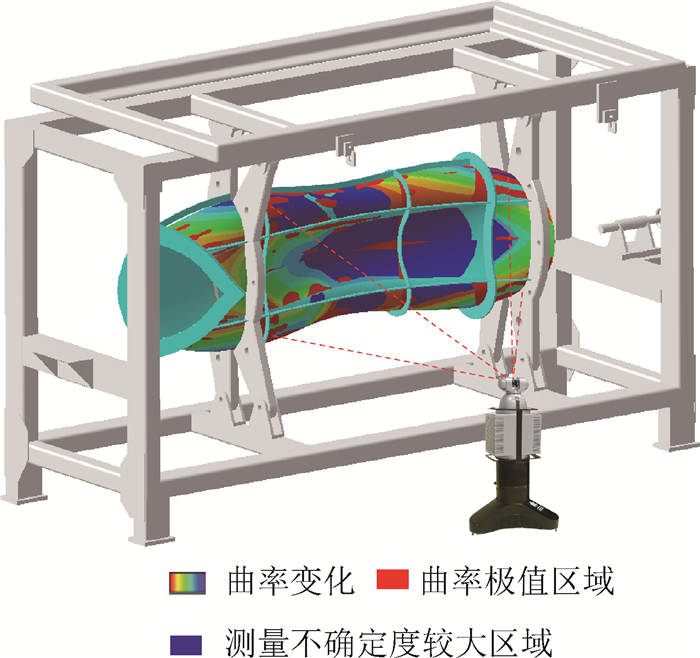
数字化测量技术在飞机大尺寸零部件检测的应用日益广泛，合理规划测量点数量和分布以精确地描述待测特征已成为关键问题之一。针对复杂曲线曲面的测量点规划问题，提出了一种基于确定性表达的测量点差异性规划方法。利用非均匀有理B样条（NURBS）理论精确拟合自由曲线，通过粒子群优化算法综合优化控制点及权因子，构建高精度的拟合曲线。提出了面向曲率特性和测量不确定度的布点策略，结合曲面特性建立完整、高效的测量点规划流程。基于CAA模块程序化实现了测量点规划方法，并以试验件为验证对象，验证了所提方法的可行性和系统的有效性。
- 数字化测量 /
- 测量点规划 /
- 曲线参数化 /
- 测量不确定度 /
- 曲率极值点
Abstract:
Digital measurement technology has been gradually applied in aircraft large-scale component measurement, which also brings about many issues, and the fundamental one is how to plan the number and layout of measurement points to well describe the curve or surface. Aimed at solving the issue of complicated curve or surface measurement points planning, a novel difference measurement points planning method based on deterministic representation is proposed. The curve's deterministic representation is acquired by using Non-Uniform Rational B-Splines (NURBS) theory, and the particle swarm optimization is adopted to optimize the control points and corresponding weights factors to construct the high-precision fitting curve. Two different measurement point planning strategies considering curvature and measurement uncertainty are designed, and combined with surface characteristics, a complete and high efficiency measurement point planning process is constructed. The measurement points planning algorithm proposed in this paper is programmed based on the CAA, and by taking test piece as experiment object, the feasibility of the algorithm and the effectiveness of the system are verified.
- digital measurement /
- measurement points planning /
- curve parameterization /
- measurement uncertainty /
- curvature extreme points

HTML全文

图 1 试验件测量不确定度及曲率分布

Figure 1. Measurement uncertainty and curvature distribution of test piece

下载: 全尺寸图片幻灯片

图 2 权因子对曲线形状的影响

Figure 2. Influence of weight factor on curve shape

下载: 全尺寸图片幻灯片

图 3 曲率极值点搜索

Figure 3. Search of curvature extreme points

下载: 全尺寸图片幻灯片

图 4 曲线曲率极值点求解结果

Figure 4. Solving result of curve curvature extreme points

下载: 全尺寸图片幻灯片

图 5 不确定度椭球模型

Figure 5. Uncertainty ellipsoid model

下载: 全尺寸图片幻灯片

图 6 曲线轮廓度公差带及测量不确定度允差

Figure 6. Tolerance zone and measurement uncertainty tolerance of curve

下载: 全尺寸图片幻灯片

图 7 曲面轮廓度公差带及测量不确定度允差

Figure 7. Tolerance zone and measurement uncertainty tolerance of surface

下载: 全尺寸图片幻灯片

图 8 测量点布设流程

Figure 8. Process of measurement points distribution

下载: 全尺寸图片幻灯片

图 9 自动布点模块架构

Figure 9. Architecture of automatic points distribution module

下载: 全尺寸图片幻灯片

图 10 试验件局部曲面片布点过程

Figure 10. Points distribution process of partial surface of test piece

下载: 全尺寸图片幻灯片

图 11 不同布点密度布点结果对比

Figure 11. Comparison of points distribution under different measurement points density

下载: 全尺寸图片幻灯片

图 12 试验件测量点分布

Figure 12. Measurement points distribution of test piece

下载: 全尺寸图片幻灯片

表 1 粒子群优化算法参数

Table 1. Parameters of particle swarm optimization algorithm

参数	数值
c₁、c₂	2.05
v_max、v_min	0.01
w	0.9
N_p	200

下载: 导出CSV

表 2 不同布点密度下测量结果对比

Table 2. Comparison of measurement result under different measurement points density

布点密度	布点数量	测量时长/min	重构孔洞数量	拟合精度/mm
20×20	8 868	98	21	0.037 3
本文密度	9 986	110	5	0.019 4
10×10	19 958	220	4	0.015 6

下载: 导出CSV

参考文献(20)

[1]	CHO M W, LEE H, YOON G S, et al.A feature-based inspection planning system for coordinate measuring machines[J].International Journal of Advanced Manufacturing Technology, 2005, 26(9-10):1078-1087.
[2]	LEE G, MOU J, SHEN Y.Sampling strategy design for dimensional measurement of geometric features using coordinate measuring machine[J].International Journal of Machine Tools & Manufacture, 1997, 37(7):917-934.
[3]	宋占杰, 张美, 何改云, 等.基于质心Voronoi结构的自由曲面布点策略[J].吉林大学学报(工学版), 2013, 43(1):34-38. SONG Z J, ZHANG M, HE G Y, et al.Sculptured surface point distribution strategy based on Voronoi tessellation[J].Journal of Jilin University(Engineering and Technology Edition), 2013, 43(1):34-38(in Chinese).
[4]	刘红军, 叶文静, 纪俐.基于实时重构的自由曲面自适应布点方法[J].中国机械工程, 2017, 28(17):2090-2094. LIU H J, YE W J, JI L.Adaptive distribution of inspection points for free-form curved surfaces based on real-time reconstruction[J].China Mechanical Engineering, 2017, 28(17):2090-2094(in Chinese).
[5]	张虎, 张润, 于连栋.基于CAD模型的三坐标测量机测量点分布规划[J].自动化与仪表, 2019, 34(2):1-4. ZHANG H, ZHANG R, YU L D.Measurement point distribution planning of coordinate measuring machine based on CAD model[J].Automation & Instrumentation, 2019, 34(2):1-4(in Chinese).
[6]	闫如忠, 张文辉.基于离散曲率的自由曲面自适应测量技术[J].制造业自动化, 2018, 40(4):153-156. YAN R Z, ZHANG W H.An adaptive measurement technology of free-form surface based on dispersed curvature[J].Manufacturing Automation, 2018, 40(4):153-156(in Chinese).
[7]	魏栋.面向复杂曲面加工的NURBS曲线逼近及插补算法研究[D].杭州: 浙江大学, 2017. WEI D.Research on NURBS curve approximation and interpolation algorithm for complex surface machining[D].Hangzhou: Zhejiang University, 2017(in Chinese).
[8]	朱心雄.自由曲线曲面造型技术[M].北京:科学出版社, 2000:152-160. ZHU X X.Free curve and surface modeling technology[M].Beijing:Science Press, 2000:152-160(in Chinese).
[9]	JAUCH J, BLEIMUND F, RHODE S, et al.Recursive B-spline approximation using the Kalman filter[J].Engineering Science and Technology, an International Journal, 2017, 20(1):28-34.
[10]	闫艳.NURBS曲线形状修改的研究[D].郑州: 郑州大学, 2012. YAN Y.The research on the modification of NURBS curves[D].Zhengzhou: Zhengzhou University, 2012(in Chinese).
[11]	KENNEDY J, EBERHART R.Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks.Piscataway: IEEE Press, 2002: 1942-1948.
[12]	韩志仁, 王刚, 彩辉, 等.基于CATIA/CAA的复杂边界平面和曲面自动布点技术研究[J].制造业自动化, 2017, 39(9):59-63. HAN Z R, WANG G, CAI H, et al.Research on generating point automaticly in complex boundary plane and surface based on CATIA/CAA[J].Manufacturing Automation, 2017, 39(9):59-63(in Chinese).
[13]	陈维桓.微分几何[M].北京:北京大学出版社, 2006:23-47. CHEN W H.Differential geometry[M].Beijing:Peking University Perss, 2006:23-47(in Chinese).
[14]	黄鹏, 王青, 李江雄, 等.激光跟踪仪三维坐标转换综合优化方法[J].计算机集成制造系统, 2015, 21(11):2912-2920. HUANG P, WANG Q, LI J X, et al.Comprehensive optimization for three-dimension coordinate transformation of laster tracker[J].Computer Intergrated Manufacturing System, 2015, 21(11):2912-2920(in Chinese).
[15]	PREDMORE C R. Bundle adjustment of multi-position measurements using the Mahalanobis distance[J].Precision Engineering, 2010, 34(1):113-123.
[16]	DENG Z, LI S, HUANG X.Uncertainties evaluation of coordinate transformation parameters in the large-scale measurement for aircraft assembly[J].Sensor Review, 2018, 38(4):542-550.
[17]	DENG Z, LI S, HUANG X.Coordinate transformation uncertainty analysis and reduction using hybrid reference system for aircraft assembly[J].Assembly Automation, 2018, 38(4):487-496.
[18]	ZABOTIN I, KAZAEVA K E.The procedure for the complete updating of immersive sets in one cutting plane method[J].Journal of Physics:Conference Series, 2019, 1158:042041.
[19]	张俐, 江春, 李承文.CATIA平台下的机身数字化对接测量软件开发与应用[J].制造业自动化, 2017, 39(2):129-133. ZHANG L, JIANG C, LI C W.Measurement software development and application of fuselage docking with CATIA platform[J].Manufacturing Automation, 2017, 39(2):129-133(in Chinese).
[20]	张辉, 李泷杲.基于CATIA二次开发的制动盘摩擦半径计算技术研究[J].制造业自动化, 2018, 40(2):74-76. ZHANG H, LI S G.Research on friction radius calculation of brake disc based on secondary development of CATIA[J].Manufacturing Automation, 2018, 40(2):74-76(in Chinese).