非线性多目标概率约束规划免疫优化算法

张仁崇; 张著洪

doi:10.13700/j.bh.1001-5965.2019.0350

非线性多目标概率约束规划免疫优化算法

doi: 10.13700/j.bh.1001-5965.2019.0350

张仁崇¹,
张著洪^2, ,

1.
贵州商学院计算机与信息工程学院, 贵阳 550014
2.
贵州大学大数据与信息工程学院, 贵阳 550025

基金项目:

国家自然科学基金 61563009)

贵州省教育厅青年科技人才成长项目 QJH KY Zi[2018] No.276

贵州省大数据应用工程研究中心 QJH KY Zi[2017] No.022

详细信息

作者简介:
张仁崇男, 硕士, 助教。主要研究方向:智能优化算法

张著洪男, 教授, 博士, 博士生导师。主要研究方向:控制理论与计算智能

通讯作者:
张著洪, E-mail: zhzhang@gzu.edu.cn

中图分类号: TP301.6
计量
- 文章访问数: 779
- HTML全文浏览量: 185
- PDF下载量: 489
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-03
- 录用日期: 2019-09-27
- 网络出版日期: 2020-05-20

Immune optimization algorithm for nonlinear multi-objective probabilistic constrained programming

ZHANG Renchong¹,
ZHANG Zhuhong^{2
, ,}

1.
Computer and Information Engineering College, Guizhou University of Commerce, Guiyang 550014, China
2.
College of Big Data and Information Engineering, Guizhou University, Guiyang 550025, China

Funds:

National Natural Science Foundation of China 61563009)

Youth Science and Technology Talent Development Project of Education Department in Guizhou Province QJH KY Zi[2018] No.276

Guizhou Big Data Application Engineering Research Center in Guizhou Province QJH KY Zi[2017] No.022

More Information

Corresponding author: ZHANG Zhuhong, E-mail: zhzhang@gzu.edu.cn

摘要

摘要:
针对噪声信息未知的一般非线性多目标概率约束规划（MOPCP）问题，探讨基于危险理论的多目标免疫优化算法（MOIOA）。算法设计中，借助自适应采样方法估计机会约束的概率和目标值；借助危险理论蕴含的应答模式分割进化种群为已感染、易感染和未感染子群；借助二进制交叉、自适应变异概率、多项式变异策略平衡种群的全局与局部搜索能力。与7种算法相比较获得的数值结果表明，所提算法的搜索效率有明显优势且搜索效果有一定的优越性，同时对复杂工程问题有应用潜力。
- 多目标概率约束规划(MOPCP) /
- 免疫优化 /
- 危险理论 /
- 自适应采样 /
- 随机模拟
Abstract:
This paper investigates a Multi-Objective Immune Optimization Algorithm (MOIOA) based on danger theory to solve the problem of nonlinear Multi-Objective Probabilistic Constrained Programming (MOPCP) with unknown noise information. In the design of the algorithm, adaptive sampling methods are used to estimate each chance constraint's probability and objective values, while each evolving population is divided into infected, susceptible and uninfected sub-populations in terms of one specific immune response mechanism contained by danger theory. The capability of global and local search can be enhanced, relying upon simulated binary crossover, adaptive mutation probability and polynomial mutation strategy. Numerical experiment results show that the proposed multi-objective algorithm has high efficiency and has some advantages over seven comparative methods with regard to solution quality. It has application potential to complex engineering problems.
- Multi-Objective Probabilistic Constrained Programming (MOPCP) /
- immune optimization /
- danger theory /
- adaptive sampling /
- stochastic simulation

HTML全文

图 1 MOIOA的流程图

Figure 1. Flowchart of MOIOA

下载: 全尺寸图片幻灯片

图 2 问题1的非支配面比较与CD、CS值的箱线图比较

Figure 2. Comparison of Pareto fronts and comparison of box plots on CD and CS for Problem 1

下载: 全尺寸图片幻灯片

图 3 问题2的非支配面比较与CD、CS值的箱线图比较

Figure 3. Comparison of Pareto fronts and comparison of box plots on CD and CS for Problem 2

下载: 全尺寸图片幻灯片

图 4 问题3的非支配面与CD、CS值的箱线图比较

Figure 4. Comparison of Pareto fronts and comparison of box plots on CD and CS for Problem 3

下载: 全尺寸图片幻灯片

图 5 问题4的非支配面与CD、CS值的箱线图比较

Figure 5. Comparison of Pareto fronts and comparison of box plots on CD and CS for Problem 4

下载: 全尺寸图片幻灯片

图 6 MOIOA的不同参数设置及统计结果比较

Figure 6. Different parameter settings of MOIOA and comparison of statistical results

下载: 全尺寸图片幻灯片

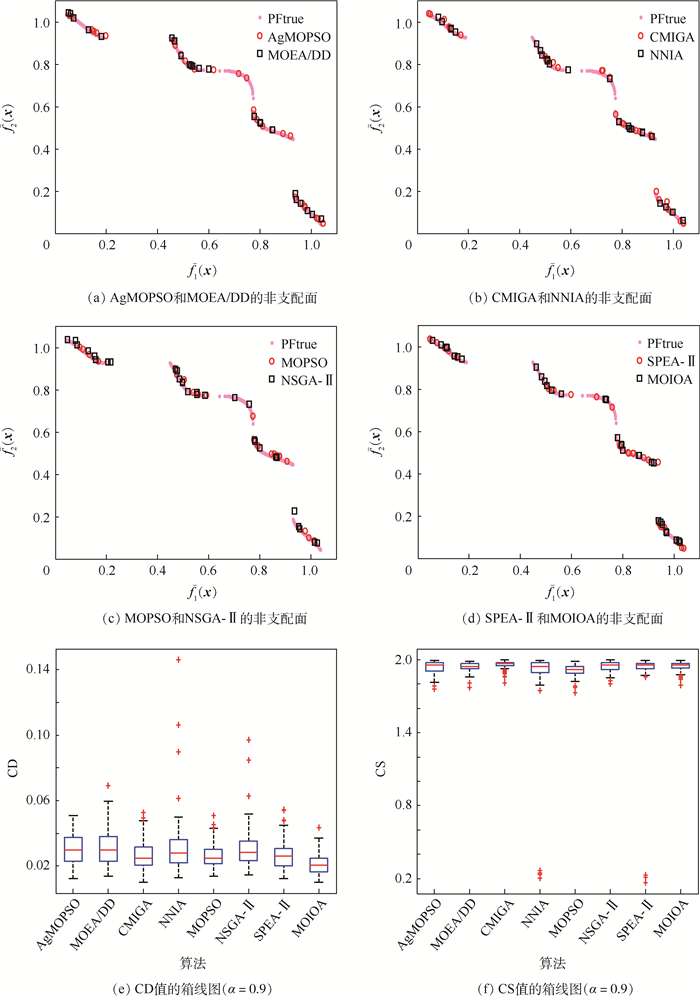
表 1 不同算法在α=0.9下求解问题1获得的统计结果比较

Table 1. Comparison of statistical results of different algorithms for Problem 1 with α = 0.9

算法	CR均值/%								CD均值	CS均值	IAE 均值/ 10^-3	FR 均值/ %	AR 均值/ s
算法	AgMOPSO	MOEA/DD	CMIGA	NNIA	MOPSO	NSGA-Ⅱ	SPEA-Ⅱ	MOIOA	CD均值	CS均值	IAE 均值/ 10^-3	FR 均值/ %	AR 均值/ s
AgMOPSO	0	14.69	16.47	14.29	20.49	15.67	15.89	18.68	0.031	1.94	5.59	63.32	19.82
MOEA/DD	14.99	0	16.73	14.44	20.61	14.38	15.72	18.14	0.031	1.94	4.05	69.34	9.24
CMIGA	16.10	17.18	0	15.66	21.02	15.60	15.60	20.69	0.027	1.96	3.98	70.83	15.02
NNIA	13.27	14.13	15.40	0	19.83	13.56	12.77	17.61	0.032	1.82	5.82	59.50	11.13
MOPSO	12.64	13.92	14.11	12.69	0	13.28	12.49	17.57	0.026	1.91	3.90	71.96	8.63
NSGA-Ⅱ	14.21	15.41	15.89	14.81	21.20	0	14.27	19.68	0.031	1.95	4.82	64.73	8.73
SPEA-Ⅱ	13.86	14.78	16.55	14.71	20.38	14.11	0	20.00	0.027	1.89	4.03	68.73	9.38
MOIOA	14.46	14.78	15.29	12.05	20.35	13.44	14.24	0	0.021	1.94	2.33	80.21	1.22

下载: 导出CSV

表 2 不同算法在α=0.9下求解问题2获得的统计结果比较

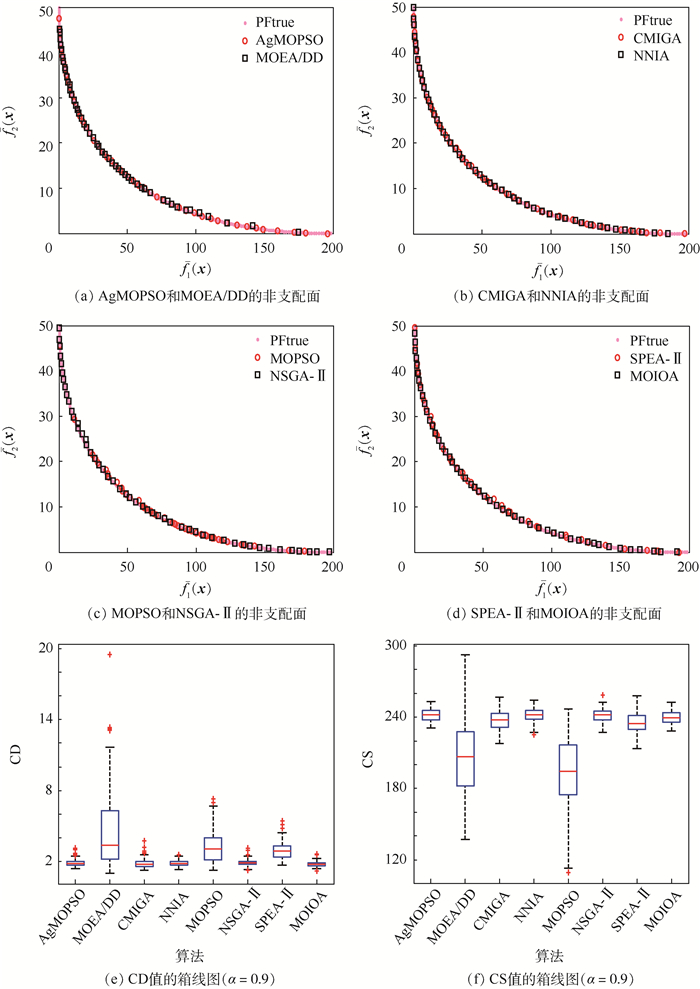
Table 2. Comparison of statistical results of different algorithms for Problem 2 with α=0.9

算法	CR均值/%								CD均值	CS均值	IAE 均值/ 10^-5	FR 均值/ %	AR 均值/ s
算法	AgMOPSO	MOEA/DD	CMIGA	NNIA	MOPSO	NSGA-Ⅱ	SPEA-Ⅱ	MOIOA	CD均值	CS均值	IAE 均值/ 10^-5	FR 均值/ %	AR 均值/ s
AgMOPSO	0	11.77	12.99	9.09	12.89	13.01	24.37	9.07	1.92	241.73	0.39	99.96	20.31
MOEA/DD	3.51	0	10.94	7.08	11.51	11.22	21.44	7.01	4.60	206.70	0.33	99.98	11.35
CMIGA	4.85	10.22	0	7.55	10.27	10.69	21.01	7.17	1.86	237.76	0.48	99.98	17.44
NNIA	4.87	10.97	11.22	0	10.85	11.08	21.79	7.62	1.86	241.21	0.84	99.94	12.36
MOPSO	2.76	9.37	8.63	5.80	0	9.09	17.09	5.76	3.30	192.67	0.30	99.96	11.24
NSGA-Ⅱ	4.49	9.59	9.94	7.39	10.17	0	19.38	7.94	1.91	241.74	0.38	99.96	11.19
SPEA-Ⅱ	2.66	8.07	7.14	4.73	7.93	7.83	0	4.78	2.93	234.86	0.55	99.98	11.30
MOIOA	4.89	10.75	11.30	7.96	11.02	11.40	22.35	0	1.79	239.55	0	100	1.80

下载: 导出CSV

表 3 不同算法在α=0.6下求解问题3获得的统计结果比较

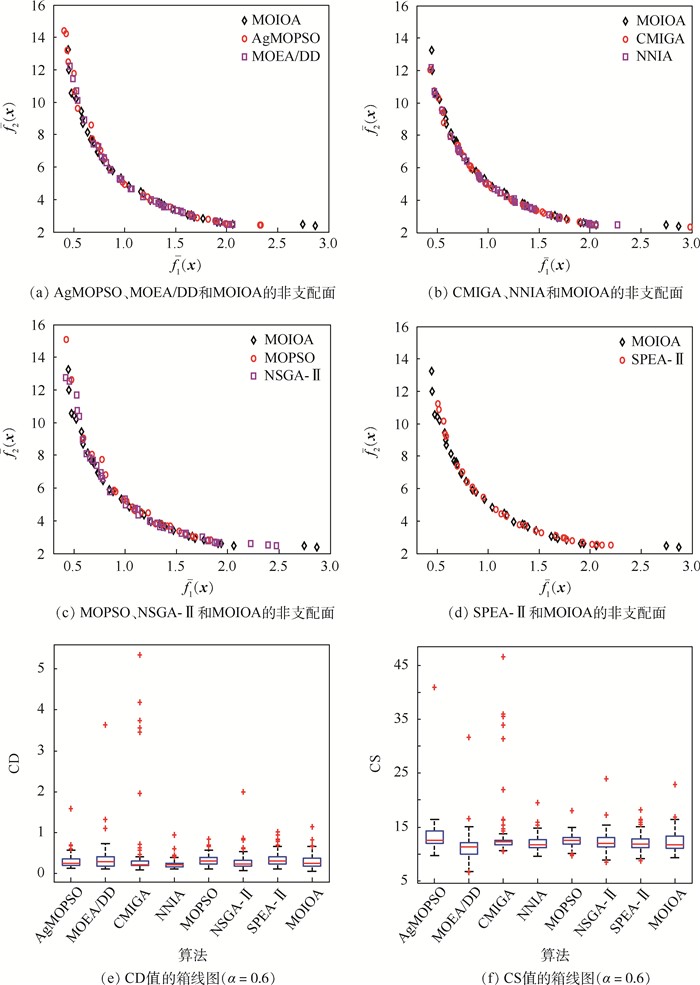
Table 3. Comparison of statistical results of different algorithms for Problem 3 with α=0.6

算法	CR均值/%								CD均值	CS均值	IAE 均值/ 10^-4	FR 均值/ %	AR 均值/ s
算法	AgMOPSO	MOEA/DD	CMIGA	NNIA	MOPSO	NSGA-Ⅱ	SPEA-Ⅱ	MOIOA	CD均值	CS均值	IAE 均值/ 10^-4	FR 均值/ %	AR 均值/ s
AgMOPSO	0	15.61	8.54	18.39	34.82	18.91	21.89	17.39	0.32	13.22	6.61	96.07	26.04
MOEA/DD	24.41	0	9.39	21.02	40.11	21.33	25.70	21.82	0.37	11.26	4.50	97.46	12.20
CMIGA	39.40	30.80	0	34.64	58.93	35.43	41.33	33.28	0.46	13.54	1.70	98.80	20.26
NNIA	25.46	18.23	10.43	0	42.59	21.80	27.97	22.05	0.24	12.06	5.39	96.87	15.19
MOPSO	12.65	7.73	2.75	8.57	0	8.90	11.15	10.12	0.33	12.49	4.80	97.72	11.84
NSGA-Ⅱ	25.38	17.63	9.61	21.25	41.64	0	26.49	21.43	0.29	12.25	4.65	97.28	11.68
SPEA-Ⅱ	20.32	14.28	5.97	17.14	34.82	16.37	0	16.95	0.36	12.17	5.09	97.02	12.69
MOIOA	27.48	20.02	11.06	23.03	42.77	23.89	29.08	0	0.31	12.36	2.18	98.58	2.48

下载: 导出CSV

表 4 不同算法在α=0.9下求解问题4获得的统计结果比较

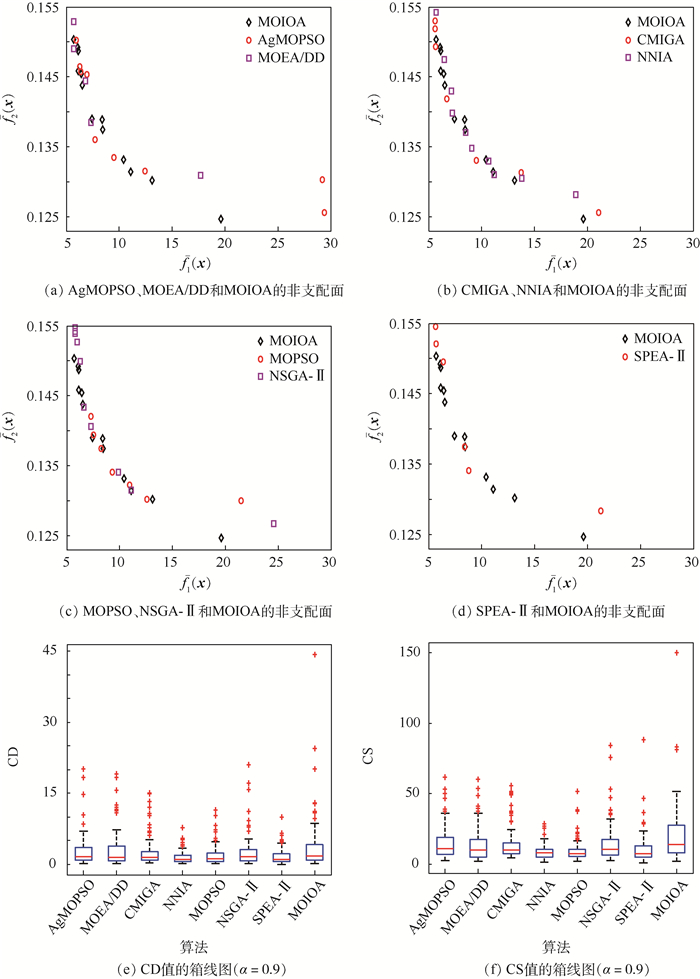
Table 4. Comparison of statistical results of different algorithms for Problem 4 with α=0.9

算法	CR均值/%								CD均值	CS均值	IAE 均值/ 10^-3	FR 均值/ %	AR 均值/ s
算法	AgMOPSO	MOEA/DD	CMIGA	NNIA	MOPSO	NSGA-Ⅱ	SPEA-Ⅱ	MOIOA	CD均值	CS均值	IAE 均值/ 10^-3	FR 均值/ %	AR 均值/ s
AgMOPSO	0	25.95	21.47	36.51	36.93	32.80	32.84	18.10	2.82	14.94	4.32	71.46	19.07
MOEA/DD	21.79	0	21.66	35.11	36.69	30.20	31.52	17.44	2.99	13.28	0.72	92.35	8.89
CMIGA	25.36	32.19	0	44.98	40.99	34.27	37.27	21.84	2.69	14.30	0.63	90.18	15.34
NNIA	13.89	22.31	13.93	0	23.90	20.88	20.60	10.41	1.50	8.51	1.13	89.42	10.69
MOPSO	11.42	16.62	11.97	27.90	0	22.47	22.90	11.81	1.85	9.33	1.38	86.03	8.83
NSGA-Ⅱ	16.58	21.04	15.69	32.40	30.78	0	24.92	15.61	2.77	14.84	0.70	92.61	9.01
SPEA-Ⅱ	16.00	20.58	18.07	34.25	32.22	28.31	0	15.07	1.66	10.70	0.94	90.15	9.68
MOIOA	29.50	36.62	30.45	49.04	45.93	41.06	40.74	0	3.78	20.12	0.80	90.04	1.30

下载: 导出CSV

参考文献(48)

[1]	李晓娜.不确定环境下城市需水量预测及多水源联合供水调度研究[D].邯郸: 河北工程大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10076-1018036022.htm LI X N.Study on urban water demand forecast and multiple water sources optimization allocation under uncertainty[D].Handan: Hebei University of Engineering, 2018(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10076-1018036022.htm
[2]	张铭鑫, 张玺, 彭建刚, 等.不确定环境下再制造加工车间多目标调度优化方法[J].合肥工业大学学报(自然科学版), 2016, 39(4):433-439. doi: 10.3969/j.issn.1003-5060.2016.04.001 ZHANG M X, ZHANG X, PENG J G, et al.Multi-objective optimization method of remanufacturing processing workshop scheduling under uncertain conditions[J].Journal of Hefei University of Technology(Natural Science), 2016, 39(4):433-439(in Chinese). doi: 10.3969/j.issn.1003-5060.2016.04.001
[3]	谢仕炜, 胡志坚, 宁月.考虑最优负荷削减方向的电网多目标分层随机机会约束规划[J].电力自动化设备, 2017, 37(8):35-42. http://d.old.wanfangdata.com.cn/Periodical/dlzdhsb201708006 XIE S W, HU Z J, NING Y.Multi-objective hierarchical stochastic chance-constrained programming considering optimal load-shedding direction[J].Electric Power Automation Equipment, 2017, 37(8):35-42(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/dlzdhsb201708006
[4]	LIU X J, ZHANG M M, SU H, et al.A multi-objective chance-constrained programming approach for uncertainty-based optimal nutrients load reduction at the Watershed Scale[J].Water, 2017, 9(5):322. doi: 10.3390/w9050322
[5]	李整.基于粒子群优化算法的机组组合问题的研究[D].北京: 华北电力大学(北京), 2016. http://cdmd.cnki.com.cn/Article/CDMD-11412-1016270824.htm LI Z.Unit commitment via particle swarm optimization algorithm[D].Beijing: North China Electric Power University(Beijing), 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-11412-1016270824.htm
[6]	QIN X S, HUANG G H, LIU L.A genetic-algorithm-aided stochastic optimization model for regional air quality management under uncertainty[J].Air Repair, 2010, 60(1):63. doi: 10.3155/1047-3289.60.1.63
[7]	BISWAL M P, BISWAL N P, LI D.Probabilistic linear programming problems with exponential random variables:A technical note[J].European Journal of Operational Research, 1998, 111(3):589-597. doi: 10.1016/S0377-2217(97)90319-2
[8]	GOICOECHEA A, DUCKSTEIN L.Nonnormal deterministic equivalents and a transformation in stochastic mathematical programming[J].Applied Mathematics & Computation, 1987, 21(1):51-72. doi: 10.1023/B:EARE.0000017275.44350.e5
[9]	韩其恒, 唐万生, 李光泉.机会约束下的投资问题[J].系统工程学报, 2002, 17(1):87-92. doi: 10.3969/j.issn.1000-5781.2002.01.017 HAN Q H, TANG W S, LI G Q.Chance-constrained portfolio problem[J].Journal of Systems Engineering, 2002, 17(1):87-92(in Chinese). doi: 10.3969/j.issn.1000-5781.2002.01.017
[10]	AĞPAK K, GÖKCEN H.A chance-constrained approach to stochastic line balancing problem[J].European Journal of Operational Research, 2007, 180(3):1098-1115. doi: 10.1016/j.ejor.2006.04.042
[11]	HESTERBERG T.Weighted average importance sampling and defensive mixture distributions[J].Technometrics, 1995, 37(2):185-194. doi: 10.1080/00401706.1995.10484303
[12]	LOUGHLIN D H, RANJITHAN S R.Chance-constrained genetic algorithms[C]//Proceedings of Genetic and Evolutionary Computation Conference.San Francisco: Morgan Kaufmann Publishers Inc., 1999: 369-376.
[13]	ZHANG Z H.Noisy immune optimization for chance-constrained programming problems[J].Applied Mechanics and Materials, 2011, 48:740-744. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.4028/www.scientific.net/AMM.48-49.740
[14]	YANG K, ZHANG Z H, LU J X.Adaptive racing ranking-based immune optimization approach solving multi-objective expected value programming[J].Soft Computing, 2018, 22(7):2139-2158. doi: 10.1007/s00500-016-2467-5
[15]	ZHANG Z H, WANG L, LIAO M.Adaptive sampling immune algorithm solving joint chance-constrained programming[J].Journal of Control Theory and Applications, 2013, 11(2):237-246. doi: 10.1007/s11768-013-1186-z
[16]	YANG K, ZHANG Z H.Adaptive sampling detection based immune optimization approach and its application to chance constrained programming[M]//SUN H, YANG C Y, LIIN C W, et al.Genetic and evolutionary computing.Berlin: Springer, 2015: 19-28.
[17]	ZHANG Z H, YANG K, ZHANG D M.Sample bound estimate based chance-constrained immune optimization and its applications[J].International Journal of Automation and Computing, 2016, 13(5):468-479. doi: 10.1007/s11633-016-0997-z
[18]	张国新, 王瑜, 沈田双.空降地面作战突破点决策模型[J].火力与指挥控制, 2010, 35(11):54-57. doi: 10.3969/j.issn.1002-0640.2010.11.016 ZHANG G X, WANG Y, SHEN T S.A study on breakthrough point decision model of airborne ground operation[J].Fire Control & Command Control, 2010, 35(11):54-57(in Chinese). doi: 10.3969/j.issn.1002-0640.2010.11.016
[19]	XU J P, DING C.A class of chance constrained multiobjective linear programming with birandom coefficients and its application to vendors selection[J].International Journal of Production Economics, 2011, 131(2):709-720. doi: 10.1016/j.ijpe.2011.02.020
[20]	白牧可, 唐巍, 张璐, 等.基于机会约束规划的DG与配电网架多目标协调规划[J].电工技术学报, 2013, 28(10):346-354. doi: 10.3969/j.issn.1000-6753.2013.10.041 BAI M K, TANG W, ZHANG L, et al.Multi-objective coordinated planning of distribution network incorporating distributed generation based on chance constrained programming[J].Transactions of China Electrotechnical Society, 2013, 28(10):346-354(in Chinese). doi: 10.3969/j.issn.1000-6753.2013.10.041
[21]	DU H, MA H, LI X.Fuzzy bi-objective chance-constrained programming model for timetable optimization of a bus route[C]//UK Workshop on Computational Intelligence.Berlin: Springer, 2017: 312-324.
[22]	刘文学, 梁军, 负志皓, 等.基于可信理论的多目标模糊机会约束无功优化[J].电工技术学报, 2015, 30(21):82-89. doi: 10.3969/j.issn.1000-6753.2015.21.010 LIU W X, LIANG J, FU Z H, et al.Multi-objective chance constrained optimal reactive power flow based on credibility theory[J].Transactions of China Electrotechnical Society, 2015, 30(21):82-89(in Chinese). doi: 10.3969/j.issn.1000-6753.2015.21.010
[23]	裴文杰, 汪沨, 谭阳红, 等.含光伏分布式电源配电网的电动汽车充电站机会约束规划[J].电力系统及其自动化学报, 2017, 29(6):45-52. doi: 10.3969/j.issn.1003-8930.2017.06.007 PEI W J, WANG F, TAN Y H, et al.Chance-constrained programming for electric vehicle charging stations in distribution network containing photovoltaic distributed generations[J].Proceedings of the CSU-EPSA, 2017, 29(6):45-52(in Chinese). doi: 10.3969/j.issn.1003-8930.2017.06.007
[24]	VIRIVINTI N, MITRA K.Intuitionistic fuzzy chance constrained programming for handling parametric uncertainty:An industrial grinding case study[J].Industrial & Engineering Chemistry Research, 2015, 54(24):6291-6304. doi: 10.1021/ie504109v
[25]	MEHLAWAT M K, GUPTA P.COTS products selection using fuzzy chance-constrained multiobjective programming[J].Applied Intelligence, 2015, 43(4):732-751. doi: 10.1007/s10489-015-0673-y
[26]	TIMMIS J, HONE A, STIBOR T, et al.Theoretical advances in artificial immune systems[J].Theoretical Computer Science, 2008, 403(1):11-32. doi: 10.1016/j.tcs.2008.02.011
[27]	GONG M, JIAO L, DU H, et al.Multiobjective immune algorithm with nondominated neighbor-based selection[J].Evolutionary Computation, 2008, 16(2):225-255. doi: 10.1162/evco.2008.16.2.225
[28]	MARTINEZ- PENALOZA M, MEZURA-MONTES E.Immune generalized differential evolution for dynamic multi-objective environments:An empirical study[J].Knowledge-Based Systems, 2018, 142:192-219. doi: 10.1016/j.knosys.2017.11.037
[29]	XIA X, ZHOU Y.On the effectiveness of immune inspired mutation operators in some discrete optimization problems[J].Information Sciences, 2018, 426:87-100. doi: 10.1016/j.ins.2017.10.038
[30]	SALMON H M, DE FARIASB C M, LOUREIRO P, et al.Intrusion detection system for wireless sensor networks using danger theory immune-inspired techniques[J].International Journal of Wireless Information Networks, 2013, 20(1):39-66. doi: 10.1007/s10776-012-0179-z
[31]	XU Q Y.Collision avoidance strategy optimization based on danger immune algorithm[J].Computers & Industrial Engineering, 2014, 76:268-279. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b148acf8f1163d70b319abf7eacdd9ac
[32]	ZHANG Z H, YUE S G, LIAO M, et al.Danger theory based artificial immune system solving dynamic constrained single-objective optimization[J].Soft Computing, 2014, 18(1):185-206. doi: 10.1007/s00500-013-1048-0
[33]	ZHANG Z H, WANG L, LONG F.Immune optimization approach solving multi-objective chance-constrained programming[J].Evolving Systems, 2013, 6(1):41-53. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0234375333/
[34]	ZHANG Z H, TU X.Probabilistic dominance-based multi-objective immune optimization algorithm in noisy environments[J].Journal of Computational and Theoretical Nanoscience, 2007, 4(7):1380-1387. doi: 10.1166/jctn.2007.2428
[35]	LIU B D.Theory and practice of uncertain programming[M].2nd ed.Berlin:Springer, 2009:50-53.
[36]	MATZINGER P. Tolerance, danger, and the extended family[J].Annual Review of Immunology, 1994, 12(1):991-1045. doi: 10.1146/annurev.iy.12.040194.005015
[37]	LIN Q Z, CHEN J Y, ZHAN Z H, et al.A hybrid evolutionary immune algorithm for multiobjective optimization problems[J].IEEE Transactions on Evolutionary Computation, 2016, 20(5):711-729. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=25089d928695dde5ccf77091c1587d65
[38]	DEB K, PRATAP A, AGARWAL S, et al.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197. doi: 10.1109/4235.996017
[39]	ZHU Q L, LIN Q Z, CHEN W N, et al.An external archive-guided multiobjective particle swarm optimization algorithm[J].IEEE Transactions on Cybernetics, 2017, 47(9):2794-2808. doi: 10.1109/TCYB.2017.2710133
[40]	LI K, DEB K, ZHANG Q F, et al.An evolutionary many-objective optimization algorithm based on dominance and decomposition[J].IEEE Transactions on Evolutionary Computation, 2015, 19(5):694-716. doi: 10.1109/TEVC.2014.2373386
[41]	QIAN S Q, YE Y Q, JIANG B, et al.Constrained multiobjective optimization algorithm based on immune system model[J].IEEE Transactions on Cybernetics, 2016, 46(9):2056-2069. doi: 10.1109/TCYB.2015.2461651
[42]	COELLO C A C, PULIDO G T, LECHUGA M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation, 2004, 8(3):256-279. doi: 10.1109/TEVC.2004.826067
[43]	ZITZLER E, LAUMANNS M, THIELE L.SPEA2: Improving the strength Pareto evolutionary algorithm[C]//Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems.Berlin: Springer, 2002: 95-100.
[44]	POOJARI C A, VARGHESE B.Genetic algorithm based technique for solving chance constrained problems[J].European Journal of Operational Research, 2008, 185(3):1128-1154. doi: 10.1016/j.ejor.2006.06.045
[45]	张著洪, 黄席樾.一种新的免疫算法及其在多模态函数优化中的应用[J].控制理论与应用, 2004(1):17-21. doi: 10.3969/j.issn.1000-8152.2004.01.006 ZHANG Z H, HUANG X Y.Novel immue algorithm and its application to multi-modal function optimization[J].Control Theory & Applications, 2004(1):17-21(in Chinese). doi: 10.3969/j.issn.1000-8152.2004.01.006
[46]	DE CASTRO L N, VON ZUBEN F J.The clonal selection algorithm with engineering applications[C]//Proceedings of Genetic and Evolutionary Computation Conference.San Fransisco: Morgan Kaufman Publisher Inc., 2000: 36-37.
[47]	DEB K. Constrained multi-objective evolutionary algorithm[M]//BANSAL J C, SINGH P K, PAL N R.Evolutionary and swarm intelligence.Berlin: Springer, 2019: 85-118.
[48]	SADOLLAH A, ESKANDAR H, KIM J H.Water cycle algorithm for solving constrained multi-objective optimization problems[J].Applied Soft Computing, 2015, 27:279-298. doi: 10.1016/j.asoc.2014.10.042