基于复杂网络的空中交通复杂性识别方法

吴明功; 叶泽龙; 温祥西; 蒋旭瑞

doi:10.13700/j.bh.1001-5965.2019.0354

基于复杂网络的空中交通复杂性识别方法

doi: 10.13700/j.bh.1001-5965.2019.0354

吴明功^{1, 2},
叶泽龙^{1, 2, 3},
温祥西^{1, 2, ,},
蒋旭瑞⁴

1.
空军工程大学空管领航学院, 西安 710051
2.
国家空管防相撞技术重点实验室, 西安 710051
3.
中国人民解放军95178部队, 南宁 530049
4.
中国人民解放军94116部队, 和田 848000

基金项目:

国家自然科学基金 71801221

陕西省自然科学研究计划 2018JQ7004

详细信息

作者简介:
吴明功  男, 硕士, 教授, 硕士生导师。主要研究方向:空中交通管理、管制指挥与安全

叶泽龙  男, 硕士研究生。主要研究方向:空中交通管制指挥与安全

温祥西  男, 博士, 讲师。主要研究方向:空管自动化技术

蒋旭瑞  男, 硕士研究生。主要研究方向:冲突探测与解脱技术

通讯作者:
温祥西, E-mail: wxxajy@163.com

中图分类号: V355
计量
- 文章访问数: 849
- HTML全文浏览量: 116
- PDF下载量: 1239
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-03
- 录用日期: 2019-12-15
- 网络出版日期: 2020-05-20

Air traffic complexity recognition method based on complex networks

WU Minggong^{1, 2},
YE Zelong^{1, 2, 3},
WEN Xiangxi^{1, 2
, ,},
JIANG Xurui⁴

1.
Air Traffic Control and Navigation College, Air Force Engineering University, Xi'an 710051, China
2.
National Key Laboratory of Air Traffic Collision Prevention, Xi'an 710051, China
3.
Unit 95178 of the PLA, Nanning 530049, China
4.
Unit 94116 of the PLA, Hetian 848000, China

Funds:

National Natural Science Foundation of China 71801221

Shaanxi Province Natural Science Research Plan 2018JQ7004

More Information

Corresponding author: WEN Xiangxi, E-mail: wxxajy@163.com

摘要

摘要:
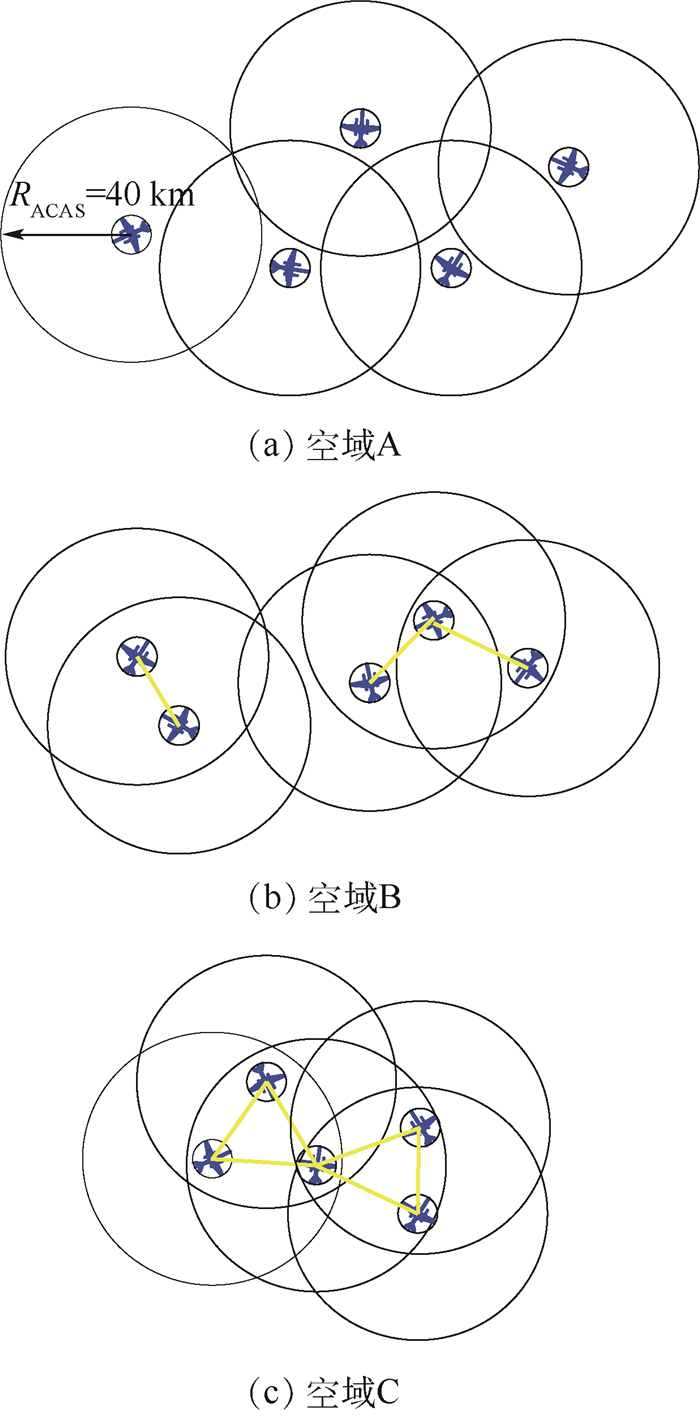
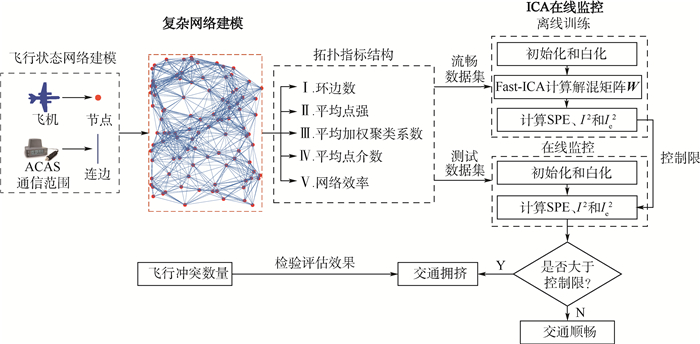
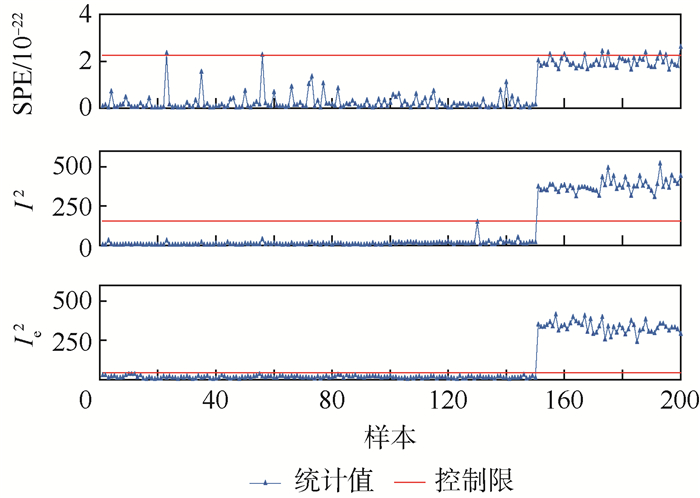
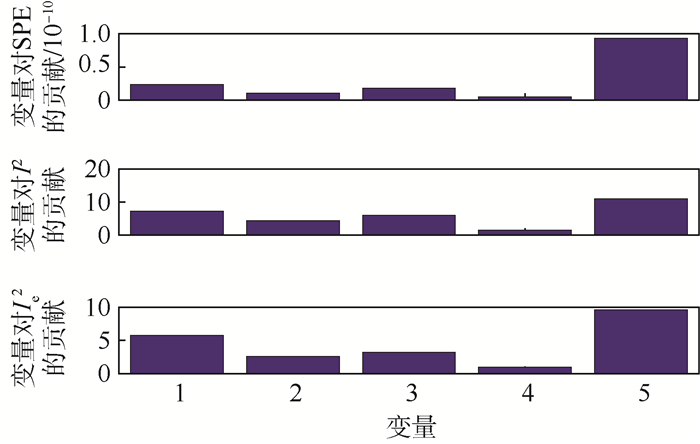
在空中交通管理中，识别空中交通复杂性是一项重要工作。目前的算法多采用飞机密度、机群、滞留程度等宏观指标对复杂性进行评价。利用复杂网络理论描述空中交通状况，将空域中的飞机视为节点，飞机与飞机之间距离小于彼此的机载防撞系统（ACAS）通信距离时开始构成连边，以此构建飞行状态复杂网络模型，可以更好地描述网络内部的微观特征。选取环边数、节点强度、平均聚类系数、介数中心性和网络效率等拓扑特性指标，对动态空中交通状况进行了研究。在此基础上，采用独立主元分析（ICA）在线识别空中交通复杂性，将交通顺畅的情况作为训练数据集进行处理，根据SPE统计量、I²统计量和I_e²统计量的变化来识别复杂性情况。仿真结果表明，所提方法可以较好地识别空中交通复杂性。
- 空中交通复杂性 /
- 交通拥堵识别 /
- 复杂网络 /
- 独立主元分析(ICA) /
- 空中交通管理
Abstract:
Identifying the complexity of air traffic is an important task in air traffic management. Most current algorithms are usually tested using some macro-indexes, such as aircraft density, aircraft clusters, stranded degree, and so on. In this paper, the air traffic situation is described from the perspective of complex networks: aircraft in airspace are regarded as nodes and edges form within Airborne Collision Avoidance System (ACAS) communication ranges. The dynamic air traffic situation is studied by selecting topological characteristic indexes such as loop numbers, node strength, average clustering coefficient, betweenness centrality and network efficiency. On this basis, Independent Component Analysis (ICA) is used to recognize air traffic complexity online and treat the smooth traffic as a training data set. The congestion is recognized according to the changes of SPE-statistic, I²-statistic and I_e²-statistic. The simulation results show that the proposed method has the ability to identify air traffic complexity well.
- air traffic complexity /
- traffic congestion identification /
- complex networks /
- Independent Component Analysis (ICA) /
- air traffic management

HTML全文

图 1 飞行状态网络结构差异性

Figure 1. Difference of flight state network structures

下载: 全尺寸图片幻灯片

图 2 边权设置

Figure 2. Edge weight setting

下载: 全尺寸图片幻灯片

图 3 本文方法主要流程

Figure 3. Main flow of proposed method

下载: 全尺寸图片幻灯片

图 4 网络结构随节点数增多的变化情况

Figure 4. Variation of network structure with increase of node number

下载: 全尺寸图片幻灯片

图 5 相同节点数不同分布时网络结构的差异

Figure 5. Difference of network structure with the same node number but different distribution of nodes

下载: 全尺寸图片幻灯片

图 6 监测图(均匀分布且节点数为50)

Figure 6. Monitoring charts (uniformly distributed and node number equals to 50)

下载: 全尺寸图片幻灯片

图 7 变量对偏差的贡献

Figure 7. Contribution of variables to deviation

下载: 全尺寸图片幻灯片

图 8 不同节点数和分布时的监测图

Figure 8. Monitoring charts with different node number and distribution

下载: 全尺寸图片幻灯片

图 9 进近阶段不同时刻雷达屏幕截图

Figure 9. Radar screenshots at different moments in phase of approaching

下载: 全尺寸图片幻灯片

图 10 进近阶段不同时刻离散子网络

Figure 10. Discrete sub-network structures at different moments in phase of approaching

下载: 全尺寸图片幻灯片

表 1 部分训练样本拓扑指标值

Table 1. Some topological indicator values of training samples

样本序号	LN	NS	CC	BC	NE
1	53	9.754 6	0.813 4	0.021 9	40.125 0
2	41	9.145 8	0.827 4	0.029 3	20.569 4
3	60	10.883 2	0.842 7	0.012 9	35.411 3
4	42	8.433 9	0.775 3	0.034 5	20.882 2
5	59	11.977 7	0.852 3	0.015 4	24.790 2
6	52	9.567 7	0.817 6	0.021 1	27.105 3
7	50	9.617 3	0.803 6	0.022 8	31.494 1
8	20	11.570 1	0.723 4	0.029 2	21.478 3
9	41	7.796 3	0.813 3	0.031 0	19.480 9
┇	┇	┇	┇	┇	┇
50	60	14.536 2	0.855 2	0.013 9	24.163 0

下载: 导出CSV

表 2 监测样本拓扑指标值和SPE、I²和I_e²统计值

Table 2. Topological indicator values of monitoring samples and statistic values of SPE, I² and I_e²

时刻序号	时刻	LN	NS	CC	BC	NE	SPE	I²	I_e²
1	15:40:43	207	23.681 4	0.934 6	0.001 3	185 983	7.467 1×10^-29	21.867 4	3.464 4
2	15:45:43	122	24.009 2	0.964 0	0.001 0	145.370 9	5.218 6×10^-29	16.758 3	4.589 4
3	15:50:43	65	18.026 1	0.951 9	0.003 5	43.537 8	3.921 4×10^-29	14.541 3	1.976 5
4	15:55:44	44	18 223	0.894 1	0.013 5	65.336 2	3.676 3×10^-29	13.287 6	5.875 4
5	16:00:43	33	8.149 0	0.884 7	0.010 1	46.486 1	9.812 5×10^-30	6.221 8	2.664 7
6	16:05:43	39	10.791 1	0.892 8	0.019 4	41.822 5	1.581 9×10^-29	7.543 9	2.545 2

下载: 导出CSV

表 3 文献[19]中K-mean算法对相同样本的复杂性识别结果

Table 3. Complexity recognition results of K-mean algorithm for the same sample in Ref.[19]

时刻序号	时刻	N	E^{1, 1}	C^{1, 1}	E^{1, 2}	C^{1, 2}	E^{2, 1}	C^{2, 1}	E^{2, 2}	C^{2, 2}	等级
1	15:40:43	24	87	0.934 6	71	0.923 8	66	0.954 7	72	0.955 8	高
2	15:45:43	18	72	0.964 0	81	0.962 7	45	0.943 1	64	0.942 5	高
3	15:50:43	14	66	0.931 9	51	0.925 4	41	0.922 1	35	0.927 6	低
4	15:55:44	13	58	0.914 1	52	0.912 4	45	0.935 0	33	0.898 8	中
5	16:00:43	11	35	0.884 7	34	0.882 1	18	0.884 6	16	0.885 6	低
6	16:05:43	12	41	0.892 8	40	0.881 7	23	0.883 2	25	0.853 0	低

下载: 导出CSV

参考文献(19)

[1]	ADAM R, JACEK S.The concept of initial air traffic situation assessment as a stage of medium-term conflict detection[J].Procedia Engineering, 2017, 187:420-424. doi: 10.1016/j.proeng.2017.04.395
[2]	PRANDINI M, PUTTA V, HU J H.A probabilistic measure of air traffic complexity in 3-D airspace[J].International Journal of Adaptive Control and Signal Processing, 2010, 24(10):813-829. doi: 10.1002/acs.1192
[3]	张进, 胡明华, 张晨.空中交通管理中的复杂性研究[J].航空学报, 2009, 30(11):2132-2142. http://d.old.wanfangdata.com.cn/Periodical/hkxb200911019 ZHANG J, HU M H, ZHANG C.Complexity research in air traffic management[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(11):2132-2142(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/hkxb200911019
[4]	张晨, 胡明华, 张进, 等.基于交通复杂性的扇区资源管理[J].南京航空航天大学学报, 2010, 42(5):607-613. http://d.old.wanfangdata.com.cn/Periodical/njhkht201005013 ZHANG C, HU M H, ZHANG J, et al.Sector asset management based on air traffic complexity[J].Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(5):607-613(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/njhkht201005013
[5]	CHEN X W, STEVEN J L, SHIMON Y N.A framework of enroute air traffic conflict detection and resolution through complex network analysis[J].Computer in Industry, 2011, 62:787-794. doi: 10.1016/j.compind.2011.05.006
[6]	WANG H Y, WEN R Y, ZHAO Y F.Analysis of topological characteristic in air traffic situation networks[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2015, 229(13):2497-2505. doi: 10.1177/0954410015578482
[7]	WANG H Y, XU X H, ZHAO Y F.Empirical analysis of aircraft clusters in air traffic situation networks[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering 2017, 231(9): 1718-1731. doi: 10.1177/0954410016660870
[8]	ZANIN M.Network analysis reveals patterns behind air safety events [J].Physica A:Statistical Mechanics and Its Applications, 2014, 401:201-206. doi: 10.1016/j.physa.2014.01.032
[9]	HYVARNEN A, OJA E.A fast fixed-point algorithm for independent component analysis[J].Neural Computation, 1997, 9:1483-1492. doi: 10.1162/neco.1997.9.7.1483
[10]	HYVARNEN A, OJA E.Independent component analysis:Algorithms and applications[J].Neural Networks, 2000, 13(4-5):411-430. doi: 10.1016/S0893-6080(00)00026-5
[11]	LEE J M, YOO C K, LEE I B.Statistical process monitoring with independent component analysis[J].Journal of Process Control, 2004, 14(5):467-485. doi: 10.1016/j.jprocont.2003.09.004
[12]	TANG J J, WANG Y H, LIU F.Characterizing traffic time series based on complex network theory[J].Physica A:Statistical Mechanics and Its Applications, 2013, 392:4192-4201. doi: 10.1016/j.physa.2013.05.012
[13]	TARJAN R.Depth-first search and linear graph algorithms[C]//Symposium on Switching & Automata Theory.Piscataway: IEEE Press, 1971: 114-121.
[14]	FREEMAN L C.A set of measures of centrality based on betweenness[J].Sociometry, 1997, 40(1):35-41. doi: 10.2307-3033543/
[15]	WANG X Y, LI J Q.Detecting communities by the core-vertex and intimate degree in complex networks[J].Physica A:Statistical Mechanics and Its Applications, 2013, 392:2555-2563. doi: 10.1016/j.physa.2013.01.039
[16]	WANG X Y, CAO J Y, LI R, et al.A preferential attachment strategy for connectivity link addition strategy in improving the robustness of interdependent networks[J].Physica A:Statistical Mechanics and Its Applications, 2017, 483:412-422. doi: 10.1016/j.physa.2017.04.128
[17]	PATERA R P.Space vehicle conflict probability for ellipsoidal conflict volumes[J].Journal of Guidance, Control, and Dynamics, 2007, 30(6):1818-1821. http://www.researchgate.net/publication/245433462_space_vehicle_conflict_probability_for_ellipsoidal_conflict_volumes
[18]	SIMOGLOU A, MARTIN E B, MORRIS A J.Statistical performance monitoring of dynamic multivariate processes using state space modelling[J].Computers & Chemical Engineering, 2002, 26(6):909-920. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ac86c9713ac3874a7c8c3a2704b2b5ab
[19]	WANG H, SONG Z, WEN R, et al.Study on evolution characteristics of air traffic situation complexity based on complex network theory[J].Aerospace Science and Technology, 2016, 58:518-528. doi: 10.1016/j.ast.2016.09.016