-
摘要:
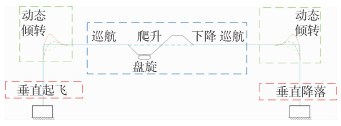
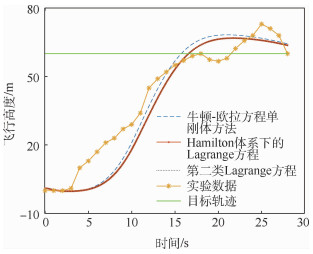
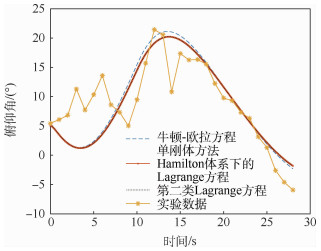
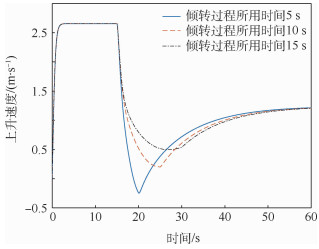
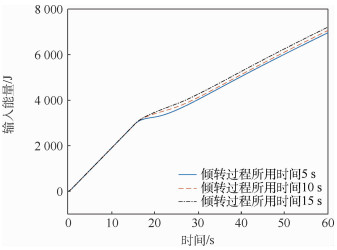
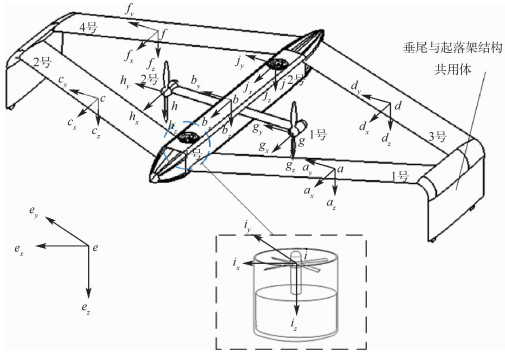
针对倾转旋翼飞行器动态倾转过程中动力学建模问题进行了研究。首先，从多体动力学出发，以某盒式倾转旋翼无人机为算例，将该无人机假设成由机翼、机体、涵道风扇、倾转旋翼等组成的多刚体系统。其次，通过不同刚体质心间的位移约束，建立该无人机系统的非保守力和力矩矩阵，以及动能、势能、余虚功和逆势能模型。最后，分别基于Hamilton体系下的Lagrange方程和第二类Lagrange方程推导并建立了该盒式倾转旋翼无人机的动力学模型。仿真结果表明：两类Lagrange方程所建动力学模型的仿真结果与实验数据一致，验证了所提建模方法的合理性；在倾转旋翼转速不变的情况下，倾转过程所用时间越长，无人机掉高越少，轨迹越光滑，但输入能量越多，具体倾转过程的设计要根据实际输入能量、倾转时间等需求进行确定。
-
关键词:
- 倾转旋翼飞行器 /
- 盒式翼布局 /
- Hamilton体系下Lagrange方程 /
- 第二类Lagrange方程 /
- 多体动力学
Abstract:The dynamics modeling of the tilt-rotor aircraft is studied during dynamic transition process. Firstly, starting from the multibody dynamics, a box-wing tilt-rotor UAV is taken as an example, which is assumed as a multi-rigid-body system consisting of wings, a body, ducted fans, tilt rotors, etc. Secondly, the non-conservative force and moment matrix of the UAV system are established by the displacement constraints of different rigid body centroids, and the kinetic energy, potential energy, complementary virtual work and inverse potential energy of the UAV are established. Finally, based on the Lagrange equation in Hamilton system and the second Lagrange equation, the dynamics model of the box-wing tilt-rotor UAV is deduced and established. The simulation results show that the simulation results of the dynamics models established by the two types of Lagrange equations are consistent with the experimental data, which verifies the rationality of the proposed modeling method. In the case that the rotation speed of the tilt rotor is constant, the longer the transition process takes, the less the UAV is dropped, the smoother the trajectory is, but the more input energy is, and the design of the specific transition process should be determined according to the actual needs of the time that the transition process takes, input energy, etc.
-
图 1 盒式倾转旋翼无人机参考坐标系示意图
Figure 1. Schematic diagram of reference coordinate systems for box-wing tilt-rotor UAV
图 3 倾转轴与无人机机体内部连接示意图
Figure 3. Schematic diagram of internal connection between tilt axis and UAV body
图 4 实验盒式倾转旋翼无人机示意图
Figure 4. Schematic diagram of experimental box-wing tilt-rotor UAV
图 5 无人机飞行高度仿真与实验结果对比
Figure 5. Comparison of UAV flight height between simulation and experimental results
图 6 无人机前飞速度仿真与实验结果对比
Figure 6. Comparison of UAV forward velocity between simulation and experimental results
图 7 无人机俯仰角仿真与实验结果对比
Figure 7. Comparison of UAV pitch angle between simulation and experimental results
表 1 盒式倾转旋翼无人机具体参数
Table 1. Specific parameters of box-wing tilt-rotor UAV
参数 数值 盒式倾转旋翼无人机最大起飞总重/kg 7.5 盒式倾转旋翼无人机机翼总面积/m2 0.8 盒式倾转旋翼无人机展长/m 2 盒式倾转旋翼无人机弦长/m 0.2 盒式倾转旋翼无人机机身长度/m 1.44 有效载荷/kg 2.5 最大升阻比 11.4 翼载荷/(kg·m-2) 8.75 
下载: 导出CSV
-
[1] 孙凯军, 张练, 付义伟, 等.某型倾转旋翼机的旋翼桨叶气动优化设计[J].航空工程进展, 2019, 10(3):340-347.SUN K J, ZHANG L, FU Y W, et al.Aerodynamic optimization design of the rotor blade of a tilt-rotor aircraft[J].Advances in Aeronautical Science and Engineering, 2019, 10(3):340-347(in Chinese). [2] XIANG Z, XU W Q, YAN S, et al.Study on the effect of tilting-rotor structure on the lift of small tilt rotor aircraft[C]//International Conference on Advanced Robotics and Mechatronics.Piscataway: IEEE Press, 2017: 380-385. [3] 曹芸芸, 陈仁良.倾转旋翼飞行器的操纵策略和配平方法[J].南京航空航天大学学报, 2009, 41(1):6-10.CAO Y Y, CHEN R L.Control strategy for tilt-rotor aircraft trimming in steady level flight[J].Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(1):6-10(in Chinese). [4] 吴翰, 王正平, 周洲, 等.多旋翼固定翼无人机多体动力学建模[J].西北工业大学学报, 2019, 37(5):928-934.WU H, WANG Z P, ZHOU Z, et al.Modeling and simulation for multi-rotor fixed-wing UAV based on multibody dynamics[J].Journal of Northwestern Polytechnical University, 2019, 37(5):928-934(in Chinese). [5] LI H X, QU X J, WANG W J.Multi-body motion modeling and simulation for tilt rotor aircraft[J].Chinese Journal of Aeronautics, 2010, 23(4):415-422. [6] SASONGKO R A, MUHAMMAD B.Modeling and simulation of rotor dynamics of a tilt-rotor aircraft[C]//International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering.Piscataway: IEEE Press, 2017: 51-56. [7] 陈建平, 宁雷鸣, 张红英, 等.基于多体动力学的大型翼伞系统飞行仿真分析[J].飞行力学, 2015, 33(6):487-490. http://www.cnki.com.cn/Article/CJFDTotal-FHLX201506002.htmCHEN J P, NING L M, ZHANG H Y, et al.Flight simulation of large parafoil-payload systems based on multibody dynamics[J].Flight Dynamics, 2015, 33(6):487-490(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-FHLX201506002.htm [8] ZHAO Z J, REN G X.Multibody dynamic approach of flight dynamics and nonlinear aeroelasticity of flexible aircraft[J].AIAA Journal, 2011, 49(1):41-53. doi: 10.2514/1.45334 [9] 周平, 梁立孚.非保守系统的Lagrange方程[J].哈尔滨工程大学学报, 2017, 38(3):452-459.ZHOU P, LIANG L F.Lagrange equation of non-conservative systems[J].Journal of Harbin Engineering University, 2017, 38(3):452-459(in Chinese). [10] 邓子辰, 于洪泳, 黄立新, 等.Hamilton体系下混凝土壳体结构的基本方程及求解方法[J].西北工业大学学报, 2005, 23(5):602-605.DENG Z C, YU H Y, HUANG L X, et al.A new systematic computational methodology for concrete shell structures[J].Journal of Northwestern Polytechnical University, 2005, 23(5):602-605(in Chinese). [11] FORBES J R, BARFOOT T D, DAMAREN C J.Dynamic modeling and stability analysis of a power-generating tumbleweed rover[J].Multibody System Dynamics, 2010, 24(4):413-439. [12] WU H, WANG Z P, ZHOU Z, et al.Modeling of small UAV parachute recovery system based on Lagrangian method[C]//International Conference on Mechatronics and Automation.Piscataway: IEEE Press, 2019: 1127-1132. [13] JIANG H B, CAO S L, CHEN Z Q.Lift and drag coefficients of flow around a flat plate at high attack angles[J].Chinese Journal of Applied Mechanics, 2011, 28(5):518-520. http://www.researchgate.net/publication/288643097_Lift_and_drag_coefficients_of_flow_around_a_flat_plate_at_high_attack_angles [14] GARRARD W L.Application of inflation theories to preliminary parachute force and stress analysis: AIAA-91-0862-CP[R].Reston: AIAA, 1991: 230-239. [15] 孙凯.涵道风扇六旋翼建模与控制技术研究[D].南京: 南京航空航天大学, 2018: 15-20.SUN K.Research on modeling and control technology of ducted fan hexrcopter[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2018: 15-20(in Chinese). [16] HOGAN F R, FORBES J R.Modeling of spherical robots rolling on generic surfaces[J].Multibody System Dynamics, 2015, 35(1):91-109. [17] MAI B, HIROSHI Y.New Lambert algorithm using the Hamilton-Jacobi-Bellman equation[J].Journal of Guidance, Control, and Dynamics, 2010, 33(3):1000-1008. [18] ANDREAS G.a Rigorous proof for the equivalence of the projective Newton-Euler equations and the Lagrange equations of second kind for spatial rigid multibody systems[J].Multibody System Dynamics, 2019, 45(1):87-103. [19] YAN L, XU W F, HU Z H, et al.Virtual-base modeling and coordinated control of a dual-arm space robot for target capturing and manipulation[J].Multibody System Dynamics, 2019, 45(4):431-455. [20] CORONEL-ESCAMILLA A, TORRES F, COMEZ-AGUILAR J F, et al.On the trajectory tracking control for an SCARA robot manipulator in a fractional model driven by induction motors with PSO tuning[J].Multibody System Dynamics, 2018, 43(3):257-277. -
下载:
点击查看大图
计量
- 文章访问数: 552
- HTML全文浏览量: 63
- PDF下载量: 168
- 被引次数: 0
