极稀疏投影数据的CT图像重建

武丽君; 孙丰荣; 杨江飞; 于倩蕾; 贺芳芳

doi:10.13700/j.bh.1001-5965.2019.0613

极稀疏投影数据的CT图像重建

doi: 10.13700/j.bh.1001-5965.2019.0613

1.
山东大学信息科学与工程学院, 青岛 266237
2.
山东大学微电子学院, 济南 250101
3.
山东大学附属山东省立医院医学影像科, 济南 250014

基金项目:

国家自然科学基金 81671703

山东省自然科学基金 ZR2019MF048

详细信息

作者简介:
武丽君女, 硕士研究生。主要研究方向:生物医学信号与信息处理

孙丰荣男, 博士, 教授。主要研究方向:CT图像重建、基于人工智能的医学影像分析与诊断

通讯作者:
孙丰荣, E-mail:sunfr_journal@163.com

中图分类号: TP391;TN911.73
计量
- 文章访问数: 804
- HTML全文浏览量: 47
- PDF下载量: 151
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-05
- 录用日期: 2020-06-12
- 网络出版日期: 2020-12-20

CT image reconstruction from ultra-sparse projection data

1.
School of Information Science and Engineering, Shandong University, Qingdao 266237, China
2.
School of Microelectronics, Shandong University, Jinan 250101, China
3.
Department of Medical Imaging, Shandong Provincial Hospital Affiliated to Shandong University, Jinan 250014, China

Funds:

National Natural Science Foundation of China 81671703

Nalural Seience Foundation of Shandong Province ZR2019MF048

More Information

Corresponding author: SUN Fengrong, E-mail:sunfr_journal@163.com

摘要

摘要:
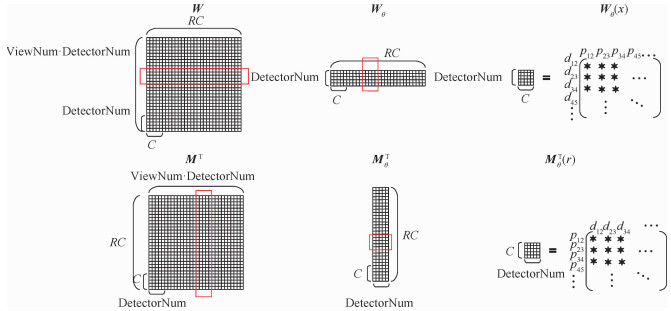
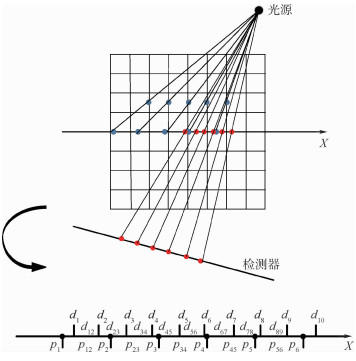
从稀疏投影数据足够精确地重建断层图像，从而能够在显著降低计算机断层成像（CT）检查X-射线辐射剂量的前提下，提供充分适宜影像学临床诊断需求的重建图像。针对圆周扫描扇束投影的二维CT图像重建，提出了投影驱动的系统模型，并将CT迭代图像重建与压缩感知（CS）理论相结合，设计了一种CT迭代图像重建算法，且将算法扩展到圆周扫描锥束投影的三维CT图像重建。仿真实验结果表明：在极稀疏投影数据的条件下（[0，2π）范围内扇束/锥束扫描不超过20个投影角度），算法数值精度高，计算复杂度低，内存开销少，有很强的工程实用性。
- 计算机断层成像(CT) /
- 图像重建 /
- 稀疏投影 /
- 投影驱动 /
- 压缩感知(CS)
Abstract:
In order to provide the reconstructed images which are suitable for the clinical imaging diagnosis, this study focuses on reconstructing the tomographic images from sparse projection data with sufficient accuracy under the premise of significantly reducing the X-ray dose of Computerized Tomography (CT) examination. Aimed at 2D image reconstruction of fan-beam projection under circular scanning, this paper proposes the view driven model and designs a CT iterative image reconstruction algorithm by combining the iterative algorithm and the Compressed Sensing (CS) theory. Then the algorithm is extended to 3D image reconstruction of cone-beam projection under circular scanning. The simulation results show that the algorithm has high numerical accuracy, low computational complexity, less memory overhead, and strong engineering practicability under the condition of ultra-sparse projection data (no more than 20 projection angles for fan-beam/cone-beam scanning in the range of[0, 2π)).
- Computerized Tomography (CT) /
- image reconstruction /
- sparse projection /
- view driven /
- Compressed Sensing (CS)

HTML全文

图 1 二维扇束投影示意图与细节图

Figure 1. Schematic diagram and detailed diagram of two-dimensional fan-beam projection

下载: 全尺寸图片幻灯片

图 2 正/反投影矩阵元素示意图

Figure 2. Schematic diagram of matrix elements of forward/backward projection

下载: 全尺寸图片幻灯片

图 3 循环2

Figure 3. Loop 2

下载: 全尺寸图片幻灯片

图 4 圆周CT扫描系统结构示意图

Figure 4. Schematic diagram of circular CT scanning system

下载: 全尺寸图片幻灯片

图 5 Shepp-Logan模型和重建图像及其中心行像素值比较

Figure 5. Shepp-Logan model and reconstructed images, as well as comparison of pixel values of center row between them

下载: 全尺寸图片幻灯片

图 6 各个投影角度数下不同算法的重建图像质量对比

Figure 6. Comparison of reconstructed image quality of different algorithms under various projection angles

下载: 全尺寸图片幻灯片

图 7 Shepp-Logan模型透视图和重建图像(第125层和128层)

Figure 7. Perspective of Shepp-Logan model and reconstructed images(125th and 128th layers)

下载: 全尺寸图片幻灯片

表 1 CT扫描参数和仿真模型信息

Table 1. CT scanning parameters and simulation model information

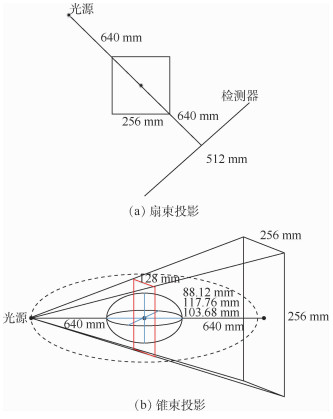
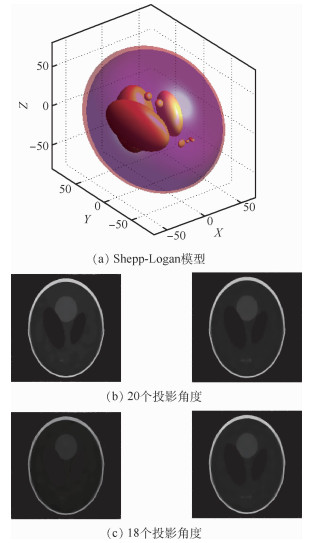
仿真参数	二维扇束	三维锥束
检测器类型	平板检测器	平板检测器
行/列检测器数	512	256
行/列检测器中心	255.5	127.5
行/列检测器间距/mm	1.0	1.0
光源到旋转中心距离/mm	640	640
旋转中心到检测器中心距离/mm	640	640
仿真模型	二维Shepp-Logan	三维Shepp-Logan模型
	模型尺寸：512×512	模型尺寸：256×256×256
	模型像素尺寸：0.5mm×0.5mm	体素尺寸：0.5mm×0.5mm×0.5mm

下载: 导出CSV

表 2 各个投影角度数下不同算法的重建结果

Table 2. Reconstruction results of different algorithms under various projection angles

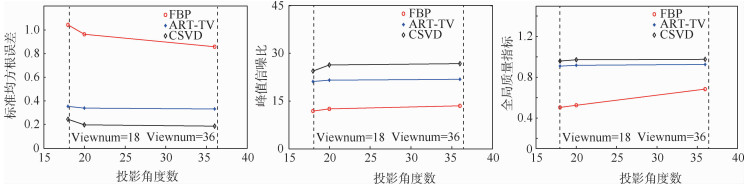
重建算法	NRMSE	PSNR	UQI	重建时间/s
FBP	0.9641	12.4663	0.5222	4.094
ART-TV	0.3387	21.5526	0.9181	69.585
CSVD	0.1958	26.3113	0.9734	32.997

下载: 导出CSV

表 3 CSVD算法重建图像质量评价

Table 3. Quality evaluation of reconstructed images using CSVD algorithm

质量评价指标	20个投影角度	18个投影角度
NRMSE	0.2887	0.2980
PSNR	22.9883	22.7137
UQI	0.9406	0.9362

下载: 导出CSV

参考文献(17)

[1]	SABA L, SURI J S.Multi-detector CT imaging principles, head, neck, and vascular systems[M].Boca Raton:CRC Press, 2013:103-122.
[2]	OHNESORGE B M, FLOHR T G, BECKER C R, et al.Multi-slice CT technology[M].Berlin:Springer, 2007:41-69.
[3]	NORELLI L J, COATES A D, KOVASZNAY B M.Cancer risk from diagnostic radiology in a deliberate self-harm patient[J].Acta Psychiatrica Scandinavica, 2010, 122(5):427-430. http://europepmc.org/abstract/MED/20136800
[4]	RAMPINELLI C, DE M P, ORIGGI D, et al.Exposure to low dose computed tomography for lung cancer screening and risk of cancer:Secondary analysis of trial data and risk-benefit analysis[J].British Medical Journal, 2017, 356(347):8. http://www.ncbi.nlm.nih.gov/pubmed/28179230
[5]	PEARCE M S, SALOTTI J A, LITTLE M P, et al.Radiation exposure from CT scans in childhood and subsequent risk of leukaemia and brain tumors:A retrospective cohort study[J]. Lancet, 2012, 380(9840):499-505. http://neuro-oncology.oxfordjournals.org/external-ref?access_num=22681860&link_type=MED
[6]	MEHYAR L S, ABU-ARJA M H, STANEK J R, et al.The risk of developing secondary central nervous system tumors after diagnostic irradiation from computed tomography in pediatrics:A literature review[J].Pediatric Neurology, 2019, 98:18-24. http://www.sciencedirect.com/science/article/pii/S0887899418311056
[7]	SIDKY E Y, KAO C M, PAN X.Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J].Journal of X-ray Science and Technology, 2006, 14(2):119-139. http://arxiv.org/abs/0904.4495
[8]	SIDKY E Y, PAN X.Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J].Physics in Medicine and Biology, 2008, 53(17):4777-4807. http://europepmc.org/articles/PMC2630711/
[9]	DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4):1289-1306.
[10]	CHEN G H, TANG J, LENG S.Prior image constrained compressed sensing (PICCS):A method to accurately reconstruct dynamic CT images from highly under-sampled projection data sets[J].Medical Physics, 2008, 35(2):660-663. doi: 10.1118/1.2836423
[11]	DEBATIN M, ZYGMANSKI P, STSEPANKOU D, et al.CT reconstruction from few-views by anisotropic total variation minimization[C]//2012 IEEE Nuclear Science Symposium and Medical Imaging Conference Record.Piscataway: IEEE Press, 2012: 2295-2296.
[12]	DEBATIN M, HESSER J.Accurate low-dose iterative CT reconstruction from few projections by generalized anisotropic total variation minimization for industrial CT[J].Journal of X-ray Science and Technology, 2015, 23(6):701-726. http://www.ncbi.nlm.nih.gov/pubmed/26756407
[13]	CANDES E, ROMBERG J, TAO T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics, 2006, 59(8):1207-1223. doi: 10.1002/cpa.20124/full
[14]	MAN B D, BASU S.Distance-driven projection and backprojection[C]//2002 IEEE Nuclear Science Symposium Conference Record.Piscataway: IEEE Press, 2002: 1477-1480.
[15]	MAN B D, BASU S.Distance-driven projection and backprojection in three dimensions[J].Physics in Medicine and Biology, 2004, 49(11):2463-2475. http://europepmc.org/abstract/med/15248590
[16]	TUY H K.An inversion formula for cone-beam reconstruction[J].SIAM Journal on Applied Mathematics, 1983, 43(3):546-552.
[17]	WANG Z, BOVIK A C.A universal image quality index[J].IEEE Signal Processing Letters, 2002, 9(3):81-84. http://www.emeraldinsight.com/servlet/linkout?suffix=b80&dbid=16&doi=10.1108%2FEC-06-2012-0145&key=10.1109%2F97.995823