-
摘要:
针对四旋翼姿态控制欠驱动、强耦合的特性,提出了一种基于线性/非线性切换自抗扰控制(SADRC)的四旋翼姿态解耦控制方法。首先,以四旋翼平台为研究对象,建立了其姿态的数学模型,引入SADRC,对基本原理进行了介绍。其次,基于SADRC设计了四旋翼姿态解耦控制器,并基于Lyapunov函数对系统进行了稳定性分析。最后,通过仿真实验对SADRC控制性能进行了验证。结果表明:SADRC在某些场合抗干扰和鲁棒性方面较线性自抗扰控制(LADRC)和非线性自抗扰控制(NLADRC)具有优势,具有工程应用的潜力。
-
关键词:
- 四旋翼 /
- 姿态控制 /
- 线性/非线性切换自抗扰控制(SADRC) /
- 稳定性分析 /
- 鲁棒性
Abstract:An Switch in linear-nonlinear Active Disturbance Rejection Control (SADRC) attitude decoupling control approach was proposed due to the underactuated, strong coupling characteristics of quadrotor. First, the mathematical model of the quadrotor attitude was formulated by taking quadrotor aircraft platform as research object. The SADRC and the basic principles of it were introduced. Then, an attitude decoupling controller based on SADRC was designed, followed by the stability analysis via Lyapunov function. Finally, the control performance of SADRC is verified by simulation experiments. The results indicate that SADRC controller possesses better performance to both Linear Active Disturbance Rejection Control (LADRC) and Nonlinear Active Disturbance Rejection Control (NLADRC) in anti-disturbance and robustness in some occasions, and has potential applications in engineering practice.
-
随着航空遥感技术的发展,在同一平台上装备多种成像载荷实现多遥感设备同时观测已成为可能,典型的如InSAR、阵列天线、可见光相机、成像光谱仪和激光雷达同时工作,由于成像载荷分布在非刚性平台的不同位置,各个遥感载荷的姿态稳定控制方式不同,每个遥感载荷都需与惯性测量单元(Inertial Measurement Unit,IMU)固联,并通过IMU进行运动信息测量,由此需形成一个分布式位置姿态测量系统(Position and Orientation System,POS)[1-3]。通常,在飞机机腹安装高精度主POS,其采用高精度IMU和GNSS进行数据融合输出高精度的时空基准信息,为分布在机翼两侧的子IMU提供基准信息。然而,由于飞机机翼不是完全刚性的,飞行过程中会受到阵风、湍流等环境因素的影响,使得机翼存在随机的柔性变形,形成的柔性杆臂误差将严重影响主POS测量信息向子IMU的传递[4-6]。针对飞机柔性变形角的特点及飞机变形建模问题,将飞机柔性变形角理想化为二阶或三阶Markov过程的方法较为常用,并将其扩充为系统状态变量进行估计和补偿。因此,为了实现主/子IMU信息的精确传递,必须在对柔性形变进行精确建模的基础上,采用高精度滤波估计方法进行误差估计和补偿[7-8]。
从系统工程实现的角度,需要考虑到子IMU的体积、质量和成本等因素,在每个子阵天线上都安装高精度IMU显然不合理[9-11]。由于安装在阵列天线上的分布式POS只能直接测量其所在的子阵天线的运动误差,不能直接测量其他未安装子IMU的子阵天线的运动误差[12-13]。如何通过分布式POS实现那些未安装子IMU的子阵天线的运动误差补偿是一个很值得研究的问题。
众所周知,机翼的形变是连续的,安装在机翼上的遥感载荷在同一时刻的运动信息可以被认为是相互关联的[14]。因此,可采用拟合的方法解决该问题[15]。本文提出了基于最小二乘拟合的全局估计方法获取未安装子IMU的遥感载荷的运动参数,并通过飞行数据的半物理仿真验证了该方法的有效性。
1. 传递对准误差模型
传递对准数学模型包括系统的状态方程及量测方程2个部分。系统的状态方程主要根据子IMU的误差传播方程来确定,包括子IMU误差方程、机翼柔性变形角方程及子IMU相对主IMU的固定安装误差角方程3个部分;而量测方程根据所选匹配方式来确定,本文选择常用的“速度+姿态”匹配方式。
1.1 机翼柔性变形角误差建模
分布式POS中,主POS一般安装在载机机腹下,子IMU一般分布安装在载机机翼的不同位置,受内外因素的影响,飞机机翼肯定存在柔性形变,这使建立主/子系统传递对准误差模型不仅要考虑固定安装误差角,还要考虑随机的柔性变形角。因此,在传递对准过程中需要对飞机的柔性变形进行估计和补偿。
机翼柔性变形建模方法的常见方法及其优缺点在引言中已经进行了比较分析,本文选择一种简单、高效的方法。将机翼柔性变形角视为二阶Markov过程,则主、子系统间的角误差模型可以表示为

(1) 式中:u=[ux, uy, uz]T为子IMU载体坐标系相对主POS载体坐标系的姿态误差角;Cba为u组成的叉乘反对称矩阵;I为3×3单位阵。
设ρ=[ρx ρy ρz]T为子IMU载体坐标系x轴、y轴和z轴上的固定安装误差角,θ=[θx θy θz]T为子IMU安装点处机翼柔性变形角。则有u=ρ+θ。
1) 固定安装误差角
固定安装误差角微分方程为

(2) 2) 柔性变形角
分布式POS中,子IMU一般安装在机翼两侧,机翼的振动及变形产生的柔性变形角主要是绕机体y轴(指向机头),同时考虑到滤波计算复杂度,所以在传递对准误差建模中只考虑绕机体坐标系y轴的柔性变形角θy。该柔性变形角可以较好地由二阶Markov过程来描述[4]:

(3) 式中:β=2.146/τ,τ为二阶Markov过程相关时间;η为零均值白噪声,其方差Qη满足:

(4) 其中:σ2为柔性变形角θy的方差;β和Qη为描述柔性变形角θy的二阶Markov过程参数。
1.2 传递对准的数学模型
本文采用“速度+姿态”的匹配方式进行传递对准,下面结合传统的IMU线性误差模型、已建立的机翼柔性变形模型和子IMU固定安装误差角模型,给出完整的分布式POS传递对准误差模型中的状态方程和量测方程,采用卡尔曼滤波(KF)方法进行状态误差估计。
1) 状态方程
根据传递对准线性误差模型,可以建立如下系统线性状态方程:

(5) 式中:f(·)由线性误差模型和上述柔性形变模型共同确定;W(k)为系统噪声向量;系统状态变量X为

(6) 其中:X1为一个15维子IMU状态变量,由平台失准角(ϕE、ϕN、ϕU)、速度误差量(δVE、δVN、δVU)、位置误差量(δL、δλ、δH)、陀螺常值漂移(εb=[εx εy εz]T)和加速度计常值偏置(▽b=[▽x ▽y ▽z]T);X2为5维子IMU载体坐标系相对主IMU载体坐标系的误差角状态变量,包括固定安装误差角ρ、子IMU载体坐标系y轴的柔性变形角θy及其一阶导数

假定系统噪声W(k)=[wεx,wεy,wεz,w▽x,w▽y,w▽z,η]T为零均值的高斯白噪声,其方差阵Q由陀螺常值漂移、加速度计常值偏置和描述柔性变形角的二阶Markov过程参数Qη共同决定。系统噪声转移矩阵G的表达式为

(7) 2) 量测方程
选择当前比较有效的“速度+姿态”匹配方式,建立传递对准数学模型的量测方程[6-7]:

(8) 式中:z=[δV′E δV′N δV′U δψ δθ δγ]T为系统的量测量,δV′E、δV′N和δV′U分别为主POS的速度经过主、子系统之间的杆臂速度补偿以后与子IMU的东向、北向和天向速度之差,δψ、δθ和δγ分别为子IMU与主IMU之间的航向角、俯仰角和横滚角之差;H为系统量测矩阵; v=[vδVE,vδVN,vδVU,vδψ,vδθ,vδγ]T为系统的量测噪声矩阵,vδVE、vδVN和vδVU分别为主节点东向、北向和天向速度的量测噪声,而vδψ、vδθ、vδγ分别为主节点航向角、俯仰角和横滚角的量测噪声。速度量测量δV′=[δV′E δV′N δV′U]的计算表达式如下:

(9) 式中:Vs和Vm分别为子IMU与主节点在各自导航坐标系下的速度;Vrnm为主/子系统之间的杆臂速度,计算表达式如下[8-9]:

(10) 式中:Cbmnm为主节点的载体坐标系到其对应的导航坐标系的方向余弦矩阵;ωibmbm为主节点的载体坐标系bm相对于惯性坐标系i的角速率在bm坐标系下的表示;rbm=[rx ry rz]T为主、子系统之间的杆臂向量在主载体坐标系bm下的表示;杆臂ṙbm的导数如下:

(11) 姿态量测量[δψ δθ δγ]T=[ψs-ψm,θs-θm,γs-γm]T表示的是主/子系统间的姿态角之差,ψs、θs和γs分别为子IMU安装点处的航向角、俯仰角和横滚角,相对应的ψm、θm和γm分别为主IMU安装点处的航向角、俯仰角和横滚角。量测矩阵H为

令主POS姿态矩阵Can=Ta,则上式中H1、H2和H3的表达式为


2. 基于最小二乘拟合法的估计方法
考虑到体积、质量和成本等因素,在所有子阵天线安装IMU是不可能的。为此,如何通过安装子IMU的测量信息预测那些未安装子IMU的子阵天线的运动信息很关键。最小二乘拟合作为一种曲线拟合方法在很多领域已经得到广泛应用。曲线拟合是用连续曲线表示离散点的坐标所组成的函数关系,其目的是根据已测量的信息建立因变量和自变量之间的函数关系。
由于机翼形变具有复杂的时空相关性,针对形变的时间相关性,可以通过主子传递对准实现。本文重点考虑同一时刻子阵天线运动信息的空间相关性。本文的核心思想是:在主/子传递对准的基础上,根据已安装子IMU的子阵天线运动信息预测未安装子IMU的运动信息。
将某时刻通过传递对准算法估计得到的安装有IMU的子阵天线处的纬度记为plat(xi)(i=1, 2, …, n′),n′为IMU个数。由最小二乘拟合法拟合得到的纬度多项式函数如下:

(12) 式中:k为拟合多项式的阶数,且满足k≤n′;ai为拟合多项式中对应的xi项的系数。在仿真实验中,有12个子阵天线和6个子IMU分布在右侧机翼上,即n′=6。因此,为了保证最小二乘拟合的精度,同样将多项式拟合的阶数k设置为6。
最小二乘拟合中误差的平方和Q可表示为

(13) 根据最小二乘拟合原理,纬度多项式函数fplat(x)需使误差的平方和Q达到最小值,即fplat(x)中的系数ai和误差的平方和Q需满足如下关系:

(14) 将式(13)代入式(14)可得

(15) 最小二乘拟合的多项式系数矩阵A=[a1 a2 … ak]T可根据式(15)求解获得,即可以得到该时刻的纬度多项式函数fplat(x)的完整表达式,进而可以根据未安装IMU的子阵天线在机翼上的坐标计算出该点在同一时刻的纬度。以此类推,可以通过最小二乘拟合法估计其余未安装IMU的子阵天线的时空信息等运动参数,最终实现阵列天线运动参数的全局估计。
3. 实验验证
为了验证本文方法的有效性,基于真实的飞行数据进行了半物理仿真验证。飞行数据来源:在陕西阎良地区进行分布式POS与InSAR联合飞行实验。主IMU安装在SAR的背面,分布式数据处理计算机放置于机舱内,用于计算并存储主POS的导航输出结果及主IMU的陀螺和加速度计输出。GNSS天线安装在飞机的背部,GNSS基准站设备固定在载机飞行区域的中心地面,如图 1所示。
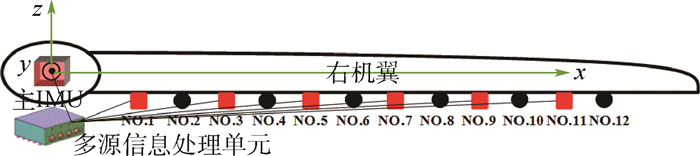
阵列天线分布示意图如图 2所示。图中主IMU安装在飞机机腹,6个红色方块表示子IMU,黑色圆形表示未安装子IMU,它们均匀安装在机翼一侧,并和主IMU一起和多源信息处理单元连接;12个子阵天线均匀分布于机翼右侧,其中12个子阵天线在机翼上的坐标如表 1所示。子阵天线No.1、No.3、No.5、No.7、No.9和No.11背面安装子IMU。该分布式系统首先在主系统和每个子IMU之间建立传递对准误差数学模型,然后通过传递对准估计出每个IMU安装处的柔性变形角,最后在已获取的柔性变形角的基础上通过最小二乘拟合出机翼上其他所有的柔性变形角,进而获取未安装子IMU的子阵天线No.2、No.4、No.6、No.8、No.10和No.12的运动参数,最终实现所有子阵天线运动参数的全局估计。
表 1 阵列天线与IMU在载体坐标系下的坐标Table 1. Coordinates of array antennas and IMUs in body coordinate子阵天线 x轴坐标/m No.1 1 No.2 2 No.3 3 No.4 4 No.5 5 No.6 6 No.7 7 No.8 8 No.9 9 No.10 10 No.11 11 No.12 12 在本次基于飞行数据的半物理仿真实验中,主POS的导航参数精度、子IMU的固定安装误差角、柔性变形角及子IMU的惯性器件常值和随机噪声的设置如下:
1) 主POS。航向角为0.005°,俯仰角和横滚角为0.002°,位置为0.05 m,速度为0.005 m/s,输出频率为20 Hz。
2) 子IMU。陀螺的常值漂移和随机漂移均为0.01(°)/h,加速度计常值偏置和随机偏置均为20 μg,输出频率为200 Hz。
3) 固定安装误差角和柔性变形角。固定安装误差角为0.5°;二阶Markov过程参数σ2是柔性变形角θy的方差,其生成规律是根据ANSYS分析出的机翼模态形状函数依次生成No.1、No.3、No.5、No.7、No.9和No.11的方差;二阶Markov过程相关时间τ=5。
本次半物理仿真实验中选择平稳飞行段的300 s数据。基于飞行数据的仿真数据生成步骤如下:
步骤1 记录本次飞行实验中主POS输出的位置、速度和姿态参数,以及主IMU输出的陀螺、加速度计的数据。
步骤2 将飞行实验中的主IMU陀螺和加速度计的数据经过固定安装误差角及柔性变形角进行转换,再叠加设定的子IMU惯性器件的常值误差和随机误差。
步骤3 将步骤2的结果作为各子IMU惯性器件输出数据。
步骤4 基准数据生成。将飞行实验中存储在主POS输出的位置、速度和姿态参数经过固定安装误差角和柔性变形角转换后得到各子IMU的位置、速度和姿态等导航参数,并作为评价传递对准估计所得的各子IMU运动参数精度的基准。
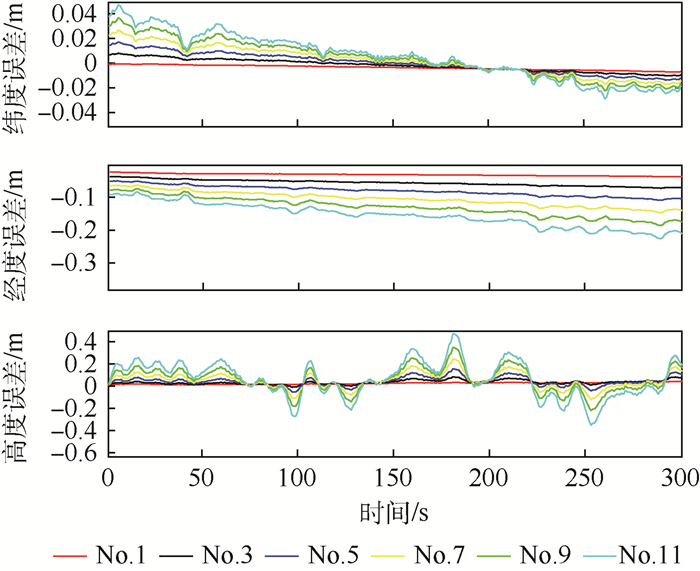
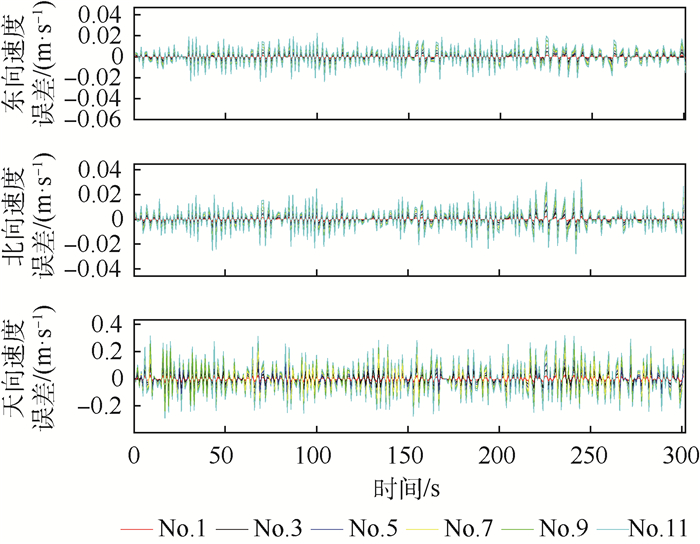
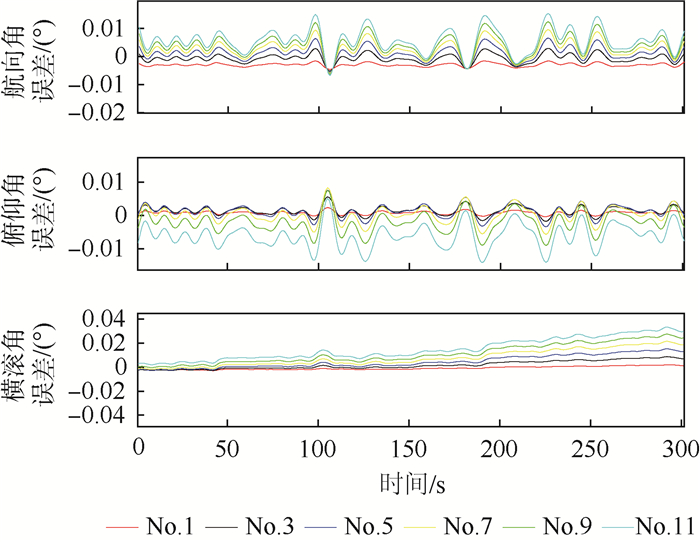
图 3~图 5给出了基于飞行实验的半物理仿真中子阵天线No.1、No.3、No.5、No.7、No.9和No.11的运动参数(位置、速度、姿态)估计结果。表 2统计了平稳飞行段300 s的RMSE。
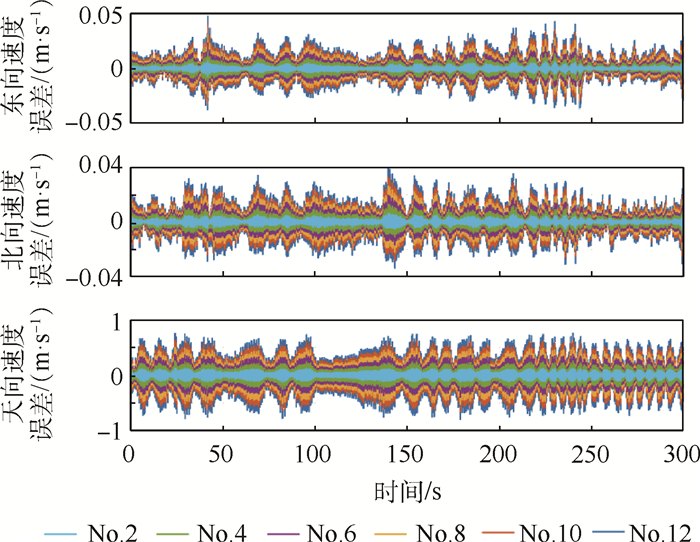
表 2 传递对准估计的子阵天线运动参数误差统计结果Table 2. Statistical results of sub-antenna motion parameter errors using transfer alignment estimation运动参数 RMSE No.1 No.3 No.5 No.7 No.9 No.11 纬度/m 0.004 6 0.009 8 0.030 4 0.043 5 0.053 0 0.076 6 经度/m 0.016 0 0.025 0 0.041 8 0.056 6 0.064 7 0.075 7 高度/m 0.015 2 0.029 6 0.032 4 0.040 3 0.051 7 0.069 1 东向速度/(m·s-1) 0.005 0.006 0.008 0.016 2 0.017 5 0.022 0 北向速度/(m·s-1) 0.004 0.006 0.009 0.019 1 0.022 0 0.025 2 天向速度/(m·s-1) 0.003 9 0.006 9 0.012 1 0.018 0 0.023 5 0.026 2 航向角/(°) 0.008 0 0.011 0 0.013 8 0.014 3 0.014 7 0.025 2 俯仰角/(°) 0.001 5 0.002 2 0.002 8 0.003 5 0.004 2 0.004 8 横滚角/(°) 0.001 3 0.002 6 0.002 8 0.003 1 0.004 4 0.004 7 表 2统计了通过传递对准获取的子阵天线运动参数的结果,采用最小二乘拟合法估计其他未安装子IMU的子阵天线运动参数。图 6~图 8给出该方法估计得到的No.2、No.4、No.6、No.8、No.10和No.12子阵天线的运动参数(位置、速度、姿态)。表 3统计了平稳段300 s的RMSE。
表 3 最小二乘拟合估计的子阵天线运动参数误差统计结果Table 3. Statistical results of sub-antenna motion parameter errors using least square fitting estimation参数 RMSE No.2 No.4 No.6 No.8 No.10 No.12 纬度/m 0.055 1 0.023 4 0.038 2 0.050 1 0.065 1 0.081 6 经度/m 0.018 8 0.038 5 0.049 6 0.060 8 0.071 8 0.085 6 高度/m 0.019 9 0.030 7 0.038 5 0.047 9 0.063 7 0.089 5 东向速度/(m·s-1) 0.004 6 0.007 2 0.011 9 0.017 4 0.021 7 0.026 9 北向速度/(m·s-1) 0.005 6 0.007 7 0.001 8 0.020 4 0.023 7 0.027 8 天向速度/(m·s-1) 0.005 1 0.010 4 0.017 2 0.020 6 0.024 4 0.028 2 航向角/(°) 0.009 0 0.013 3 0.014 0 0.016 0 0.023 3 0.028 6 俯仰角/(°) 0.001 9 0.002 4 0.003 3 0.004 0 0.004 4 0.004 8 横滚角/(°) 0.002 1 0.002 5 0.003 1 0.004 3 0.004 6 0.004 9 通过比较表 2和表 3可以看出,利用最小二乘拟合法获得的未安装子IMU的No.2、No.4、No.6、No.8、No.10和No.12子阵天线的运动参数精度与通过传递对准估计获得的No.1、No.3、No.5、No.7、No.9和No.11子阵天线的运动参数精度相当。上述统计结果进一步验证了本文提出的最小二乘拟合法估计的未安装子IMU的子阵天线运动参数的有效性。另外,分析表 2和表 3可知,离主系统越近,通过最小二乘拟合法获得的该点运动参数的精度也越高。因为离主系统越远的子节点处的柔性变形角估计误差越大,进而导致离主系统越远的子节点的运动参数估计精度越差。
4. 结论
为了能通过较少的子IMU获取更多的子节点运动信息,本文首先建立了基于二阶Markov的柔性杆臂形变模型,其次建立一个20维的传递对准误差模型,并采用高精度估计方法,最后获取了已安装IMU的子阵天线的运动参数。在此基础上,进一步提出了基于最小二乘拟合的全局估计方法获取未安装子IMU的子阵天线相位中心的运动参数,基于飞行数据的半物理仿真进行了验证,实验结果表明:
1) 能有效估计未安装子IMU的子阵天线运动参数,实现阵列天线运动参数的全局估计,且估计精度与安装子IMU的子阵天线的运动参数的精度相当,从而验证了本文方法的有效性。
2) 建立的传递对准误差模型只是考虑了一维柔性变形角,这与实际工作中的机翼形变情况还有一定差别,因此本文建立的传递对准误差模型肯定会影响全局估计精度。
-
表 1 LADRC、NLADRC、SADRC控制器参数选择
Table 1. Parameter preferences of LADRC, NLADRC, SADRC
控制器 ϕ通道 θ通道 ψ通道 LADRC[15] wo=28, wc=2.8, b0=0.424 wo=30, wc=3, b0=0.424 wo=30, wc=3.2, b0=0.213 NLADRC[14] ESO α1=0.75, α2=0.5, α3=0.25,
β01=30, β02=300, β03=1 000,
b0=0.9, δ=0.006α1=0.75, α2=0.5, α3=0.25,
β01=30, β02=300, β03=1 000,
b0=0.9, δ=0.006α1=0.75, α2=0.5, α3=0.25,
b0=0.06, δ=0.004, β01=30,
β02=300, β03=1 000NLESF δ=3,α1=0.5, α2=0.05,
β1=150, β2=120δ=3,α1=0.5, α2=0.05,
β1=150, β2=120δ=1,α1=0.5, α2=0.05,
β1=300, β2=180SADRC α1=1, α2=0.5, α3=0.25,
wc=2.8, wo=30, woN=8,
δs=0.005, b0=0.424,
δ=0.002,β01=3woN,
β02=3woN2/5, β03=woN3/9α1=1, α2=0.5, α3=0.25,
wc=3, wo=30, woN=8,
δs=0.005, b0=0.424,
δ=0.002,β01=3woN,
β02=3woN2/5, β03= w3oN/9α1=1, α2=0.5, α3=0.25,
wc=3.2, wo=8, woN=8,
δs=0.005, b0=0.213,
δ=0.002,β01=3woN,
β02=3woN2/5, β03= woN3/9注:α1、α2、α3分别为所设计控制器NLESO中非线性函数fal(e, αi, δ)对应αi(i=1, 2, 3)大小;wo和wc分别为LESO和控制器的带宽;b0为系统参数;δ和δs分别为切换自抗扰线性区间长度和切换临界值;β01、β02、β03为NLESO的增益;β1和β2分别为控制分量u0的控制律增益;woN为NLESO带宽;h为离散步长。 -
[1] 蒋回蓉, 邓志诚, 祝明, 等.变桨距四旋翼飞行器的建模与控制研究[J].电光与控制, 2015, 22(10):48-55.JIANG H R, DENG Z C, ZHU M, et al.On modeling and control of quadrotor aircraft with variable blade pitch[J].Electronics Optics & Control, 2015, 22(10):48-55(in Chinese). [2] DIERKS T, JAGANNATHAN S.Output feedback control of a quadrotor UAV using neural networks[J].IEEE Transactions on Neural Networks, 2010, 21(1):55-66. [3] 方旭, 刘金琨.四旋翼无人机动态面控制[J].北京航空航天大学学报, 2016, 42(8):1777-1784.FANG X, LIU J K.Dynamic surface control for quadrotor unmanned air vehicle[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8):1777-1784(in Chinese). [4] 方旭, 刘金琨.四旋翼飞行器三维航迹规划及跟踪控制[J].控制理论与应用, 2015, 32(8):1120-1128.FANG X, LIU J K.Three-dimension path planning and trajectory tracking control for quadrotor unmanned aerial vehicle[J].Control Theory & Applications, 2015, 32(8):1120-1128(in Chinese). [5] CUI R, LI Y, YAN W.Mutual information-based multi-AUV path planning for scalar field sampling using multidimensional RRT*[J].IEEE Transactions on System, Man, and Cybernetics Systems, 2016, 46(7):993-1004. [6] HE L L, BAI P, LIANG X L, et al.Feedback formation control of UAV swarm with multiple implicit leaders[J].Aerospace Science and Technology, 2018, 72:327-334. [7] 郭民环, 苏岩, 朱欣华.带吊挂负载的四旋翼无人机滚动纳什控制[J].北京航空航天大学学报, 2018, 44(11):2343-2349.GUO M H, SU Y, ZHU X H.Receding Nash control for quadrotor UAVs carrying a cable-suspended payload[J].Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(11):2343-2349(in Chinese). [8] BOUABDALLAH S, NOTH A, SIEGWART R.PID vs LQR control techniques applied to an indoor micro quadrotor[C]//2004 IEEE International Conference on Intelligent Robots and Systems.Piscataway: IEEE Press, 2004: 2451-2456. [9] BOUABDALLAH S, SIEGWART R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]//2005 IEEE International Conference on Robotics and Automation.Piscataway: IEEE Press, 2005: 2247-2252. [10] NICOL C, MACNAB C J B, RAMIREZ-SERRANO A.A robust adaptive control of a quadrotor helicopter[J].Mechatronics, 2011, 21(6):927-938. [11] 蒋回蓉.变桨距四旋翼飞行器的建模与控制研究[D].北京: 北京航空航天大学, 2014.JIANG H R.On modeling and control of quadrotor aircraft with variable blade pitch[D].Beijing: Beihang University, 2014(in Chinese). [12] 张静, 张华, 刘恒, 等.微型四旋翼无人机模糊PID控制[J].兵工自动化, 2014, 33(6):58-62.ZHANG J, ZHANG H, LIU H, et al.Fuzzy-PID control for macro-quadrotor UAV[J].Ordnance Industry Automation, 2014, 33(6):58-62(in Chinese). [13] 韩京清.自抗扰控制器及其应用[J].控制与决策, 1998, 13(1):19-23.HAN J Q.Auto-disturbance-rejection controller and its applications[J].Control and Decision, 1998, 13(1):19-23(in Chinese). [14] 李毅, 陈增强, 孙明玮, 等.离散型自抗扰控制器在四旋翼飞行姿态控制中的应用[J].控制理论与应用, 2015, 32(11):1470-1477.LI Y, CHEN Z Q, SUN M W, et al.Attitude control for quadrotor helicopter based on discrete-time active disturbance rejection control[J].Control Theory & Applications, 2015, 32(11):1470-1477(in Chinese). [15] 刘敏, 吉月辉, 李俊芳, 等.四旋翼飞行器自抗扰姿态控制[J].计算机仿真, 2016, 33(3):71-75.LIU M, JI Y H, LI J F, et al.Active disturbance rejection attitude control for quadrotor aircraft[J].Computer Simulation, 2016, 33(3):71-75(in Chinese). [16] 杨立本, 章卫国, 黄得刚.基于ADRC姿态解耦的四旋翼飞行器鲁棒轨迹跟踪[J].北京航空航天大学学报, 2015, 41(6):1026-1033.YANG L B, ZHANG W G, HUANG D G.Robust trajectory tracking for quadrotor aircraft based on ADRC attitude decoupling control[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6):1026-1033(in Chinese). [17] 李杰, 齐晓慧, 夏元清, 等.线性/非线性自抗扰切换控制方法研究[J].自动化学报, 2016, 42(2):202-212.LI J, QI X H, XIA Y Q, et al.On linear/nonlinear active disturbance rejection switching control[J].Acta Automation Sinica, 2016, 42(2):202-212(in Chinese). [18] LI J, XIA Y, QI X, et al.On the necessity, scheme, and basis of the linear-nonlinear switching in active disturbance rejection control[J].IEEE Transactions on Industrial Electronics, 2017, 64(2):1425-1435. -








 下载:
下载:








 下载:
下载: