Fault estimation method based on adaptive super-twisting sliding mode observer and unknown input observer
-
摘要:
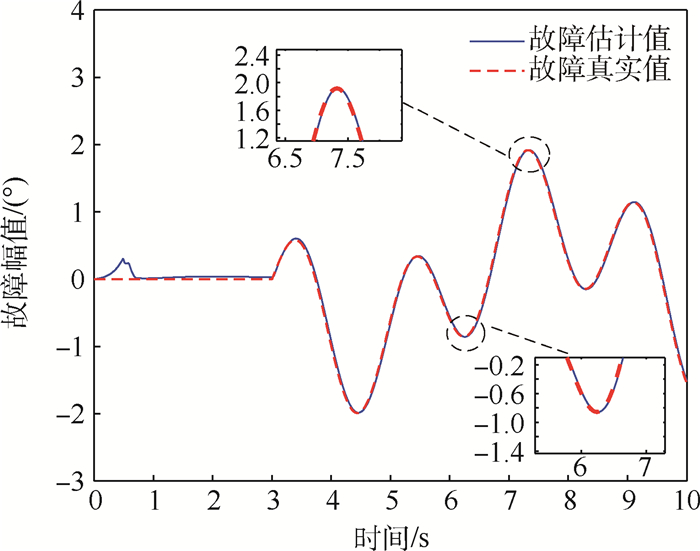
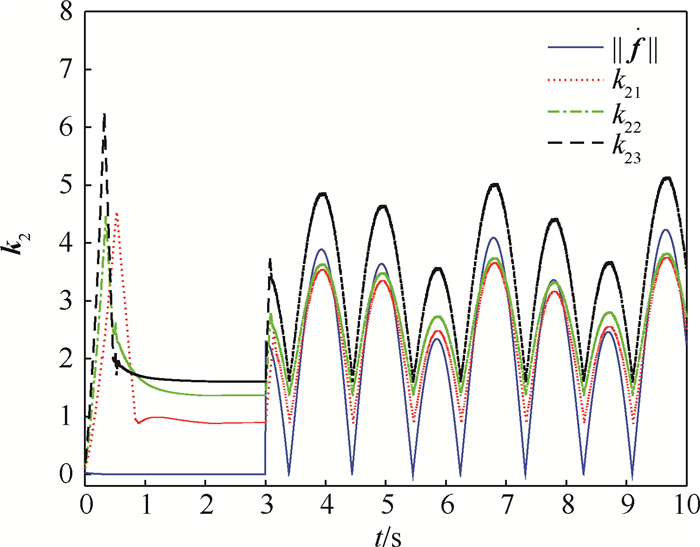
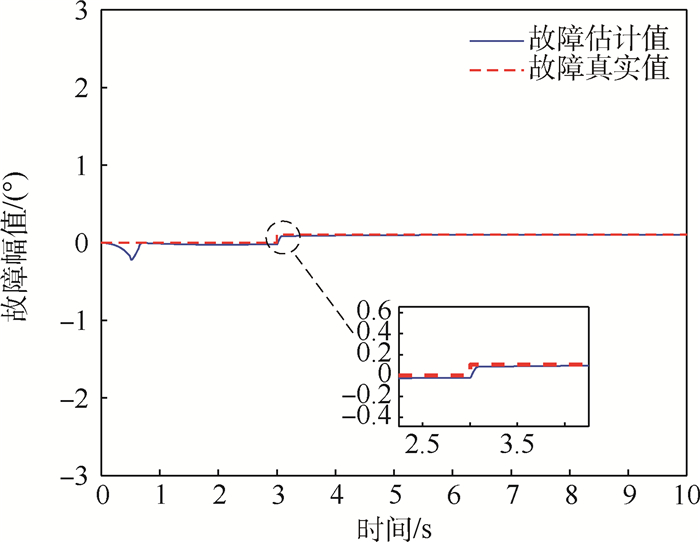
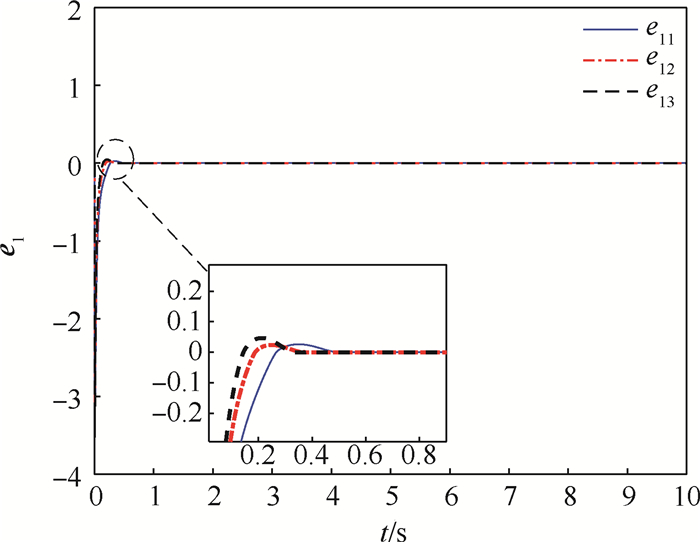
针对系统在有未知干扰情况下的故障估计问题，提出一种基于自适应Super-Twisting滑模观测器（ASTSMO）和未知输入观测器（UIO）的故障估计方法。不需要已知故障导数的上界，避免了现有自适应算法存在的滑模增益过估计问题，并且能够处理多执行器同时发生故障的情况。首先，通过非奇异变换将原系统降阶为两个子系统，其中一个子系统只受故障的影响，另一个子系统同时含有故障和不确定干扰。对两个子系统分别设计ASTSMO观测器和UIO观测器，并对误差系统有限时间内收敛的条件进行了证明，同时给出了滑模增益初始值和时变增益的设计方法。然后，基于等效控制的概念对故障进行检测和估计。最后，通过仿真算例验证了所提故障估计方法的有效性。
-
关键词:
- 故障估计 /
- Super-Twisting算法 /
- 滑模观测器(SMO) /
- 未知输入观测器(UIO) /
- 等效控制
Abstract:For the problem of fault estimation with unknown disturbance, a fault estimation method based on Adaptive Super-Twisting Sliding Mode Observer (ASTSMO) and Unknown Input Observer (UIO) is proposed. This method does not require that the upper bound of fault derivative is known, which avoids the problem of sliding-mode gain overestimation in the existing adaptive algorithms, and is able to handle simultaneous faults of multiple actuators. First, the original system is degraded to two subsystems by non-singular transformation, one of which is only affected by the fault, and the other subsystem contains both fault and uncertain interference. ASTSMO and UIO are designed for two subsystems respectively, and the error of the system of finite time convergence condition has been carried on the proof. At the same time, the initial value of sliding-mode gain and the design method of time-varying gain are given. Then, based on the concept of equivalent control, the fault is detected and estimated. Finally, a simulation example is given to verify the effectiveness of the proposed fault estimation method.
-
图 2 发生缓变故障时的子系统1状态观测误差
Figure 2. State observation error of subsystem 1 when slow-varying fault occurs
图 4 发生缓变故障时的k1自适应变化曲线
Figure 4. Adaptive change curves of k1 when slow-varying falut occurs
图 5 发生缓变故障时的k2自适应变化曲线
Figure 5. Adaptive change curves of k2 when slow-varying falut occurs
图 7 发生突变故障时的子系统1状态观测误差
Figure 7. State observation error of subsystem 1 when sudden fault occurs
图 14 执行器同时发生故障时的故障估计结果
Figure 14. Fault estimations results for simultaneous actuator failures
-
[1] PATTON R J, JIE C.Robust model-based fault diagnosis for dynamic systems[M].Boston:Kluwer Academic Publishers, 1999:1-8. [2] TAN C P, EDWARDS C.Sliding mode observers for detection and reconstruction of sensor faults[J].Automatica, 2002, 38(10):1815-1821. [3] HE J, ZHANG C.Fault reconstruction based on sliding mode observer for nonlinear systems[J].Mathematical Problems in Engineering, 2012, 2012:1-22. [4] EDWARDS C, ALWI H, TAN C.Sliding mode methods for fault detection and fault tolerant control with application to aerospace systems[J].International Journal of Applied Mathematics and Computer Science, 2012, 22(1):109-124. [5] ALWI H, EDWARDS C, TAN C P.Sliding mode estimation schemes for incipient sensor faults[J].Automatica, 2009, 45(7):1679-1685. [6] WANG L, CAI M, ZHANG H, et al.Active fault-tolerant contr-ol for wind turbine with simultaneous actuator and sensor faults[J].Complexity, 2017, 2017:1-11. [7] BEN B A, DHAHRI S, BEN H F, et al.Simultaneous actuator and sensor faults reconstruction based on robust sliding mode observer for a class of nonlinear systems[J].Asian Journal of Control, 2017, 19(1):362-371. [8] HAMDI H, RODRIGUES M, MECHMECHE C, et al.Fault diagnosis based on sliding mode observer for LPV descriptor systems[J].Asian Journal of Control, 2019, 21(1):89-98. [9] GHOLAMI S, SAHA S, ALDEEN M.Fault tolerant control of electronically coupled distributed energy resources in microgrid systems[J].International Journal of Electrical Power and Energy Systems, 2018, 95:327-340. [10] 柳春, 姜斌, 张柯, 等.带扰动的线性系统微小故障早期诊断方法[J].上海交通大学学报, 2015, 49(6):889-896.LIU C, JIANG B, ZHANG K, et al.Incipient fault detection of linear system with disturbance[J].Journal of Shang Hai Jiao Tong University, 2015, 49(6):889-896(in Chinese). [11] RAOUFI R, MARQUEZ H J, ZINOBER A S I.H∞ sliding mode observers for uncertain nonlinear lipschitz systems with fault estimation synthesis[J].International Journal of Robust and Nonlinear Control, 2010, 20(16):1785-1801. [12] 胡正高, 赵国荣, 黄婧丽, 等.基于二阶滑模观测器的连续系统故障估计[J].控制与决策, 2014, 29(12):2271-2276.HU Z G, ZHAO G R, HUANG J L, et al.Fault estimation of continuous-time systems based on second order sliding mode observation[J].Control and Decision, 2014, 29(12):2271-2276(in Chinese). [13] HUANGFU Y G, XU J, ZHAO D, et al.A novel battery state of charge estimation method based on a super-twisting sliding mode observer[J].Energies, 2018, 11(5):1211. [14] 陈诚, 韦常柱, 琚啸哲, 等.基于滑模观测补偿的四旋翼飞行器鲁棒动态逆控制[J].系统工程与电子技术, 2018, 40(1):119-126.CHEN C, WEI C Z, JU X Z, et al.Robust dynamic inversion control for quad-rotors unmanned vehicle based on sliding mode disturbance observation and compensation[J].System Engineering and Electronics, 2018, 40(1):119-126(in Chinese). [15] MOHAMED G, SOFIANE A A, NICOLAS L.Adaptive super twisting extended state observer based sliding mode control for diesel engine air path subject to matched and unmatched disturbance[J].Mathematics and Computers in Simulation, 2018, 151:111-130. [16] ZHANG M, GUAN Y, ZHAO W.Adaptive super-twisting sliding mode control for stabilization platform of laser seeker based on extended state observer[J].Optik, 2019, 199:163337. [17] HENDEL R, KHABER F, ESSOUNBOULI N.Adaptive high order sliding mode controller/observer based terminal sliding mode for MIMO uncertain nonlinear system[J/OL].International Journal of Control, 2019(2019-03-21)[2019-12-15].https://doi.org/10.1080/00207179.2019.1598580. [18] MALEKZADEH M, KARIMPOUR H.Adaptive super twisting vibration control of a flexible spacecraft with state rate estimation[J].Journal of Sound and Vibration, 2018, 422:300-317. [19] 杨雅君, 廖瑛, 尹大伟, 等.双层自适应快速super-twisting控制算法[J].控制理论与应用, 2016, 33(8):1119-1127.YANG Y J, LIAO Y, YIN D W, et al.Adaptive dual layer fast super twisting control algorithm[J].Control Theory & Applica-tions, 2016, 33(8):1119-1127(in Chinese). [20] HAUTUS M L J.Strong detectability and observers[J].Linear Algebra and its Applications, 1983, 50:353-368. [21] EDWARDS C, SHTESSEL Y.Adaptive dual-layer super-twisting control and observation[J].International Journal of Control, 2016, 89(9):1759-1766. [22] KHALIL H K.Nonlinear systems[M].Upper Saddle River:Prentice-Hall, 2002:323. [23] EDWARDS C, SPURGEON S K.On the development of discontinuous observers[J].International Journal of Control, 1994, 59(5):1211-1229. -
下载:
点击查看大图
计量
- 文章访问数: 744
- HTML全文浏览量: 135
- PDF下载量: 76
- 被引次数: 0
