考虑舵机时滞的阵风减缓主动控制律设计

杨阳; 杨超; 吴志刚; 戴玉婷

doi:10.13700/j.bh.1001-5965.2019.0635

考虑舵机时滞的阵风减缓主动控制律设计

doi: 10.13700/j.bh.1001-5965.2019.0635

北京航空航天大学航空科学与工程学院, 北京 100083

基金项目:

国家自然科学基金 11672018

详细信息

作者简介:
杨阳  男，博士研究生。主要研究方向：气动弹性力学及主动控制

杨超  男，博士，教授，博士生导师。主要研究方向：气动弹性力学与控制

吴志刚  男，博士，副教授，博士生导师。主要研究方向：气动弹性力学与控制

戴玉婷  女，博士，副教授，博士生导师。主要研究方向：气动弹性力学与控制

通讯作者:
吴志刚, E-mail: wuzhigang@buaa.edu.cn

中图分类号: V215.3
计量
- 文章访问数: 628
- HTML全文浏览量: 107
- PDF下载量: 95
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-18
- 录用日期: 2020-01-21
- 网络出版日期: 2020-12-20

Design of gust alleviation active control law considering time-delay of servo actuator

School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China

Funds:

National Natural Science Foundation of China 11672018

More Information

Corresponding author: WU Zhigang, E-mail: wuzhigang@buaa.edu.cn

摘要

摘要:
针对存在舵机时滞环节的气动伺服弹性系统，提出基于Padé近似和线性二次高斯（LQG）控制的阵风减缓主动控制律设计方法。利用Padé近似将舵机中的时滞环节线性化为一个高阶传递函数并引入气动弹性模型，建立线性的阵风减缓受控模型；利用LQG控制方法对线性化模型设计阵风减缓主动控制系统，并采用平衡截断法对所设计的控制系统进行降阶；利用Simulink将所设计的控制系统引入非线性模型中，得到von Karman连续阵风激励情况下系统的开/闭环响应情况。计算结果表明：根据所提方法设计的阵风减缓主动控制律能有效降低原气动伺服弹性系统的阵风响应，对研究对象机身过载的抑制在15%左右，而对翼根弯矩的抑制达到25%以上。
- 气动伺服弹性 /
- 阵风减缓主动控制 /
- 时间延迟 /
- Padé近似 /
- 最优控制
Abstract:
For the aersevoelastic model including servo actuators with time-delay segment, the design method of gust alleviation control system is proposed based on Padé approximation and Linear Quadratic Gaussian (LQG) control method. Padé approximation was used to linearize the time-delay segment to a high-order transfer function, and then this function was introduced to an aeroelastic model to establish a linear controlled model of gust alleviation. The LQG method was applied to design a gust alleviation control system based on the linear model, and the order of control system was reduced by the balance truncation method. By using Simulink, the designed control system was introduced to the nonlinear model to calculate the gust responses of open/closed systems under von Karman continuous gust model. The results showed that the gust alleviation control system based on the proposed method could effectively reduce the gust responses of the original model with time-delay. The overloads of the airplane were reduced by around 15% and the root bend moment was reduced by more than 25%.
- aeroservoelasticity /
- gust alleviation active control /
- time delay /
- Padé approximation /
- optimal control

HTML全文

图 1 飞翼布局飞机结构模型及传感器舵机布置

Figure 1. Structural model of flying-wing aircraft and arrangement of sensors and actuators

下载: 全尺寸图片幻灯片

图 2 包含纯时滞模型及2~6阶Padé近似模型的舵机阶跃和频率响应

Figure 2. Step and frequency responses of actuator with pure time-delay model and 2~6 order Padé approximation models

下载: 全尺寸图片幻灯片

图 3 增稳控制系统结构

Figure 3. Stability augment control system

下载: 全尺寸图片幻灯片

图 4 阵风减缓主动控制系统

Figure 4. Gust alleviation active control system

下载: 全尺寸图片幻灯片

图 5 阵风减缓主动控制系统仿真模型

Figure 5. Simulation model of gust alleviation active control system

下载: 全尺寸图片幻灯片

图 6 舵机的仿真模型

Figure 6. Simulation model of actuator

下载: 全尺寸图片幻灯片

图 7 气动伺服弹性模型的阵风响应

Figure 7. Gust responses of aeroservoelastic model

下载: 全尺寸图片幻灯片

图 8 降阶前后控制系统的频率响应

Figure 8. Frequency responses of control system before and after order reduction

下载: 全尺寸图片幻灯片

图 9 降阶前后系统回差矩阵的最小奇异值

Figure 9. Minimum singular value of closed-loop system before and after order reduction

下载: 全尺寸图片幻灯片

表 1 阵风响应的均方根及减缓效果

Table 1. Root-mean-square of gust responses and effects of gust alleviation

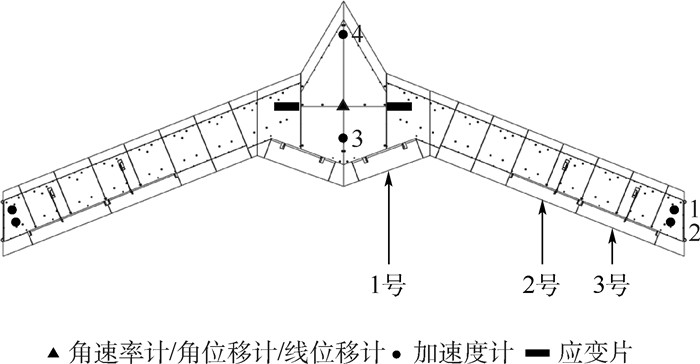
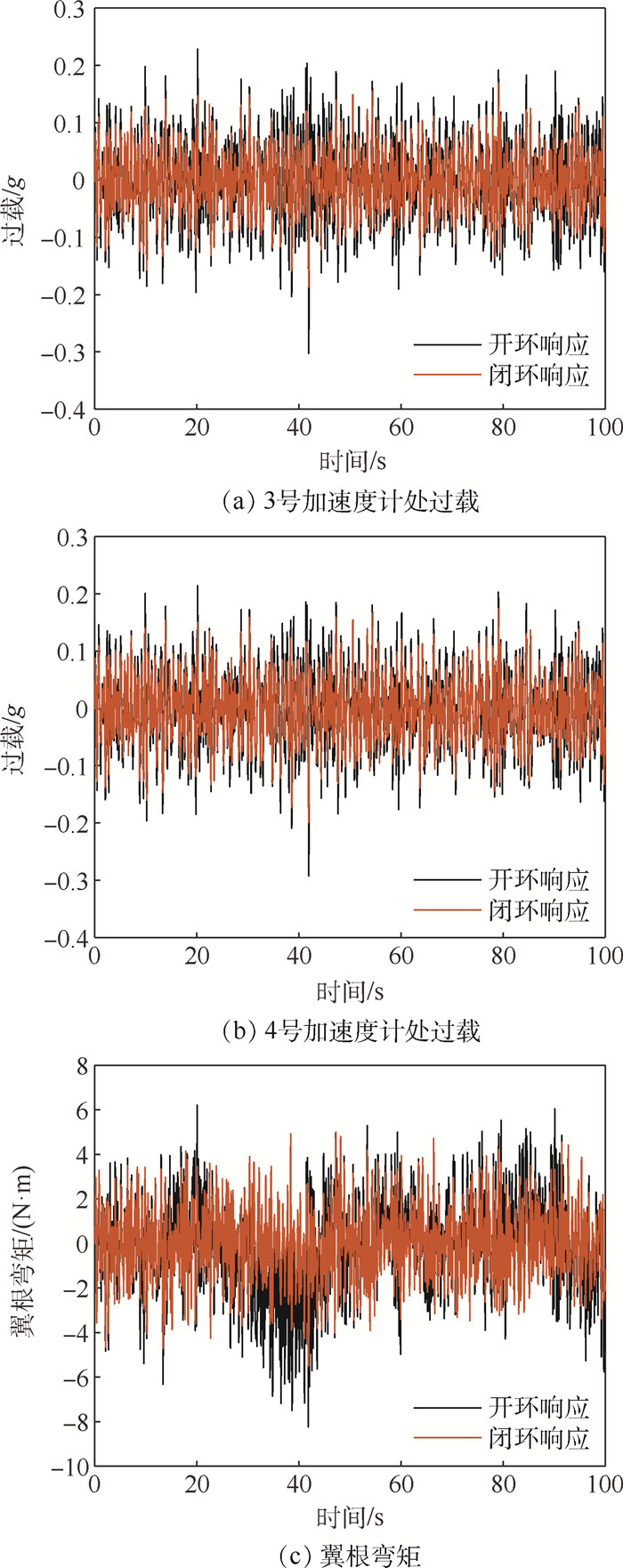
均方根	3号加速度计处过载/g	4号加速度计处过载/g	翼根弯矩/ (N·m)
开环响应	0.071 2	0.071 7	2.294 8
闭环响应	0.058 1	0.062 3	1.645 8
减缓效率/%	18.39	13.11	28.28

下载: 导出CSV

表 2 线性模型和非线性模型的阵风减缓效果

Table 2. Gust alleviation effects of linear model and nonlinear model

阵风响应	减缓效率/%
阵风响应	线性模型	非线性模型
3号加速度计处过载	18.40	18.39
4号加速度计处过载	13.16	13.11
翼根弯矩	28.30	28.28

下载: 导出CSV

表 3 不同Padé近似阶数下所设计控制系统的阵风减缓效果

Table 3. Gust alleviation effects of designed control system based on different Padé approximation orders

近似阶数	减缓效率/%
近似阶数	3号加速度计处过载	4号加速度计处过载	翼根弯矩
2	8.57	-0.28	29.73
4	19.24	13.95	29.46
6	19.66	14.64	27.67
8	19.38	14.37	28.86
10	19.38	14.37	28.39

下载: 导出CSV

表 4 控制律降阶对阵风减缓效果的影响

Table 4. Effect of order-reduction on gust alleviation

降阶阶数	减缓效率/%
降阶阶数	3号加速度计处过载	4号加速度计处过载	翼根弯矩
12	—	—	—
14	18.39	13.10	28.28
16	18.40	13.11	28.76
44	19.24	13.95	29.46
注：—表示不稳定。

下载: 导出CSV

表 5 6阶Padé近似情况下控制律降阶对阵风减缓效果的影响

Table 5. Effect of order-reduction on gust alleviation in case of 6-order Padé approximation

降阶阶数	减缓效率/%
降阶阶数	3号加速度计处过载	4号加速度计处过载	翼根弯矩
12	7.56	0.50	24.13
14	11.25	5.43	24.72
16	19.31	14.22	27.22
50	19.66	14.64	27.67

下载: 导出CSV

表 6 8阶Padé近似情况下控制律降阶对阵风减缓效果的影响

Table 6. Effect of order-reduction on gust alleviation in case of 8-order Padé approximation

降阶阶数	减缓效率/%
降阶阶数	3号加速度计处过载	4号加速度计处过载	翼根弯矩
12	7.37	12.00	25.04
14	10.70	4.35	26.09
16	19.31	14.06	28.22
56	19.38	14.37	28.86

下载: 导出CSV

参考文献(27)

[1]	WRIGHT J R, COOPER J E.飞机气动弹性力学及载荷导论[M].姚一龙, 译.上海: 上海交通大学出版社, 2010: 281-313. WRIGHT J R, COOPER J E.Introduction to aircraft aeroelasticity and loads[M].YAO Y L, translated.Shanghai: Shanghai Jiao Tong University Press, 2010: 281-313(in Chinese).
[2]	毕莹.大展弦比飞机阵风减缓设计与试验研究[D].北京: 北京航空航天大学, 2017: 1-10. BI Y.Control law and wind tunnel test about gust alleviation of high-aspect-ratio aircraft[D].Beijing: Beihang University, 2017: 1-10(in Chinese).
[3]	FULLER J R.Evolution of airplane gust loads design requirements[J].Journal of Aircraft, 1995, 32(2):235-246. doi: 10.2514/3.46709
[4]	杨俊斌, 吴志刚, 戴玉婷, 等.飞翼布局飞机阵风减缓主动控制风洞试验[J].北京航空航天大学学报, 2017, 43(1):184-191. doi: 10.13700/j.bh.1001-5965.2016.0079 YANG J B, WU Z G, DAI Y T, et al.Wind tunnel test of gust alleviation active control for flying wing configuration aircraft[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(1):184-191(in Chinese). doi: 10.13700/j.bh.1001-5965.2016.0079
[5]	LIU X, SUN Q, COOPER J E.LQG based model predictive control for gust alleviation[J].Aerospace Science and Technology, 2017, 71:499-509. http://www.sciencedirect.com/science/article/pii/S1270963817309999
[6]	COOK R G, PALACIOS R, GOULART P.Robust gust alleviation and stabilization of very flexible aircraft[J].AIAA Journal, 2013, 51(2):330-340. doi: 10.2514/1.J051697
[7]	ALAM M, HROMCIK M, HANIS T.Active gust load alleviation system for flexible aircraft:Mixed feedforward/feedback approach[J].Aerospace Science and Technology, 2015, 41:122-133. https://www.sciencedirect.com/science/article/pii/S1270963814002739
[8]	ZHAO Y H, YUE C Y, HU H Y.Gust load alleviation on a large transport airplane[J].Journal of Aircraft, 2016, 53(6):1932-1946. doi: 10.2514/1.C033713
[9]	孙玉凯, 张仁嘉, 吴志刚, 等.航模舵机的动态特性测试与系统辨识[J].北京航天航天大学学报, 2020, 46(2):294-303. http://www.cnki.com.cn/Article/CJFDTotal-BJHK202002007.htm SUN Y K, ZHANG R J, WU Z G, et al.Dynamical tests and system identification of small UAV actuators[J].Journal of Beijing University of Aeronautics and Astronaustics, 2020, 46(2):294-303(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-BJHK202002007.htm
[10]	杨建忠, 徐丹, 杨士斌, 等.考虑非线性因素的阵风减缓系统建模与仿真[J].飞行力学, 2018, 36(4):48-52. http://www.cqvip.com/QK/92336X/20184/676144681.html YANG J Z, XU D, YANG S B, et al.Modeling and simulation of gust alleviation system with system nonlinearity[J].Flight Dynamics, 2018, 36(4):48-52(in Chinese). http://www.cqvip.com/QK/92336X/20184/676144681.html
[11]	黄伟, 李芹, 王志萍.增益和相位补偿的双模Smith预估控制算法[J].上海电力学院学报, 2011, 27(6):603-607. http://www.ixueshu.com/document/0c25ea62490640e58ea228edaa6dd1f4318947a18e7f9386.html HUANG W, LI Q, WANG Z P.Research on dual-model Smith predictive control with gain and phrase compensation[J].Journal of Shanghai University of Electric Power, 2011, 27(6):603-607(in Chinese). http://www.ixueshu.com/document/0c25ea62490640e58ea228edaa6dd1f4318947a18e7f9386.html
[12]	唐功友.时滞系统的降维状态预测器及预测控制器设计[J].控制理论与应用, 2004, 21(2):295-298. http://www.cqvip.com/QK/90555X/20042/10282841.html TANG G Y.Design of reduced-order predictive state observer and predictive controller for systems with time-delay[J].Control Theory & Applications, 2004, 21(2):295-298(in Chinese). http://www.cqvip.com/QK/90555X/20042/10282841.html
[13]	唐功友, 雷靖, 孙亮.控制时滞系统基于观测器的最优扰动抑制[J].控制理论与应用, 2009, 26(2):209-214. http://d.wanfangdata.com.cn/Periodical/kzllyyy200902019 TANG G Y, LEI J, SUN L.Observer-based optimal disturbance-rejection for linear systems with time-delay in control action[J].Control Theory & Applications, 2009, 26(2):209-214(in Chinese). http://d.wanfangdata.com.cn/Periodical/kzllyyy200902019
[14]	MATEJICKOVA K, BAKOSOVA M.Robust PI controller desing for a time-delay process[C]//Proceedings of 2013 International Conference on Process Control.Piscataway: IEEE Press, 2013: 480-485.
[15]	KIM I H, JEONG G J, SON Y I.An adaptive output feedback control for time-delay systems with input disturbance[C]//Proceedings of ICROS-SICE International Joint Coferenece 2009.Piscataway: IEEE Press, 2009: 1742-1746.
[16]	NATORI K.A design method of time-delay systems with communication disturbance observer by using Padé approximation[C]//Proceedings of 2012 12th IEEE International Workshop on Advanced Motion.Piscataway: IEEE Press, 2012: 1-6.
[17]	QIAN W M, HUANG R, HU H Y, et al.Active flutter suppression of a multiple-actuated-wing wind tunnel model[J].Chinese Journal of Aeronautics, 2014, 27(6):1451-1460. https://www.sciencedirect.com/science/article/pii/S1000936114001654
[18]	吕志民, 周茂林.使用Padé近似式处理数字控制系统中的纯滞后[J].中山大学学报, 2001, 40(1):114-115. http://d.wanfangdata.com.cn/Periodical_zsdxxb200101031.aspx LÜ Z M, ZHOU M L.Manipulation of the pure time delay in digital control system applying Padé approximation[J].Acta Scientiarum Naturalium University Sunyatseni, 2001, 40(1):114-115(in Chinese). http://d.wanfangdata.com.cn/Periodical_zsdxxb200101031.aspx
[19]	DORF R C, BISHOP R H.Modern control systems[M].12th ed.Upper Saddle River:Prentice Hall, 2010:835-908.
[20]	OGATA K.Modern control engineering[M].5th ed.Upper Saddle River:Prentice Hall, 2010:751-805.
[21]	黄超.柔性飞翼飞机颤振主动抑制系统建模、设计与验证[D].北京: 北京航空航天大学, 2018: 95-99. HUANG C.Modeling, design, and verification of active flutter suppression system acting on flexible flying-wing aircraft[D].Beijing: Beihang University, 2018: 95-99(in Chinese).
[22]	熊纲, 杨超.平衡截断法在气动伺服弹性系统模型降阶中的应用[J].航空学报, 2001, 22(2):168-170. http://www.cnki.com.cn/Article/CJFDTotal-HKXB200102016.htm XIONG G, YANG C.Application of balanced truncation method on aeroservoelastic model reduction[J].Acta Aeronautic et Astronautica Sinica, 2001, 22(2):168-170(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-HKXB200102016.htm
[23]	尤明, 宗群, 曾凡琳, 等.基于平衡截断方法的高超声速飞行器模型降阶[J].控制理论与应用, 2014, 31(6):795-800. http://www.cqvip.com/QK/90555X/201406/661750519.html YOU M, ZONG Q, ZENG F L, et al.Model order reduction for hypersonic vehicle based on balanced truncate method[J].Control Theory & Applications, 2014, 31(6):795-800(in Chinese). http://www.cqvip.com/QK/90555X/201406/661750519.html
[24]	朱盟, 曹国武, 张志伟, 等.基于Levy法的气动舵机系统辨识[J].弹箭与制导学报, 2011, 31(6):69-72. http://www.cqvip.com/QK/97591A/201106/40410136.html ZHU M, CAO G W, ZHANG Z W, et al.The system identification of pneumatic actuator based on Levy method[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(6):69-72(in Chinese). http://www.cqvip.com/QK/97591A/201106/40410136.html
[25]	KARPEL M, MOULIN B.Dynamic response of aeroservoelastic systems to gust exicitation[J].Journal of Aircraft, 2005, 42(5):1264-1272. doi: 10.2514/1.6678
[26]	肖叶伦, 金长江.大气扰动中的飞行原理[M].北京:国防工业出版社, 1993:116-181. XIAO Y L, JIN C J.Flight principle in atmosphere disturbance[M].Beijing:National Defense Industry Press, 1993:116-181(in Chinese).
[27]	LEHTOMAKI N, SANDELL N, ATHANS M.Robustness results in linear-quadratic Gaussian based multivariable control designs[J].IEEE Transactions on Automatic Control, 1981, 26(2):75-93. https://ieeexplore.ieee.org/document/1102565