基于CLYC闪烁体的中子能谱测量及反演方法

侯东辉; 张珅毅; 杨祎罡; 王琦标; 张斌全; 余庆龙

doi:10.13700/j.bh.1001-5965.2019.0643

基于CLYC闪烁体的中子能谱测量及反演方法

doi: 10.13700/j.bh.1001-5965.2019.0643

侯东辉^{1, 2},
张珅毅^{1, 2,},
杨祎罡³,
王琦标⁴,
张斌全^{1, 5},
余庆龙^{1, 5}

1.
中国科学院国家空间科学中心, 北京 100190
2.
中国科学院大学, 北京 100049
3.
清华大学工程物理系, 北京 100084
4.
成都理工大学核技术与自动化工程学院, 成都 610051
5.
天基空间环境探测北京市重点实验室, 北京 100190

基金项目:

国家自然科学基金 41941001

详细信息

作者简介:
侯东辉女, 博士研究生。主要研究方向:探测器设计仿真及数据处理

张珅毅男, 博士, 研究员, 博士生导师。主要研究方向:粒子探测器设计

通讯作者:
张珅毅, E-mail: zsy@nssc.ac.cn

中图分类号: V447⁺.1
计量
- 文章访问数: 1217
- HTML全文浏览量: 124
- PDF下载量: 393
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-24
- 录用日期: 2020-04-17
- 网络出版日期: 2021-01-20

Neutron measurement and inversion based on CLYC scintillator

HOU Donghui^{1, 2},
ZHANG Shenyi^{1, 2
,},
YANG Yigang³,
WANG Qibiao⁴,
ZHANG Binquan^{1, 5},
YU Qinglong^{1, 5}

1.
National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Department of Engineering Physics, Tsinghua University, Beijing 100084, China
4.
College of Nuclear Technology and Automation Engineering, Chengdu University of Technology, Chengdu 610051, China
5.
Beijing Key Laboratory of Space Environment Exploration, Beijing 100190, China

Funds:

National Natural Science Foundation of China 41941001

More Information

Corresponding author: ZHANG Shenyi, E-mail: zsy@nssc.ac.cn

摘要

摘要:
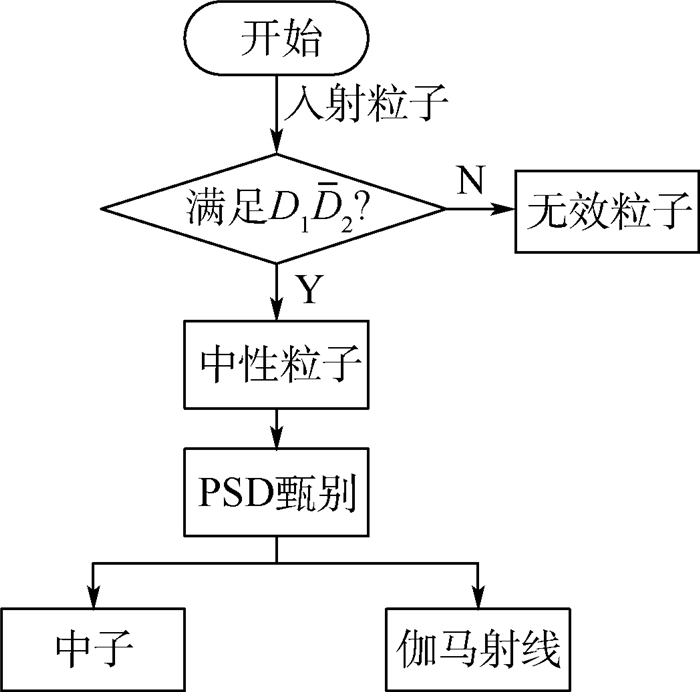
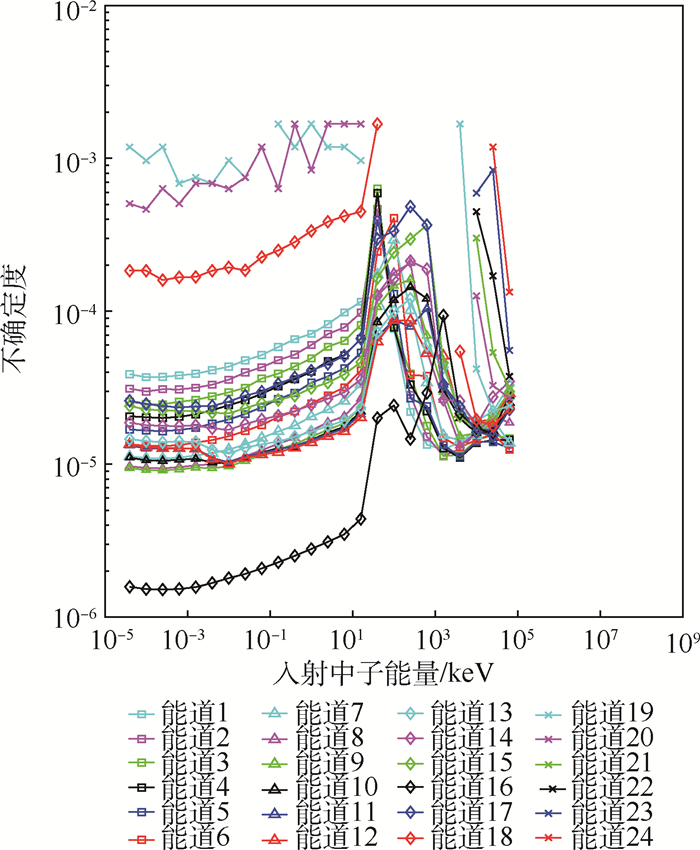
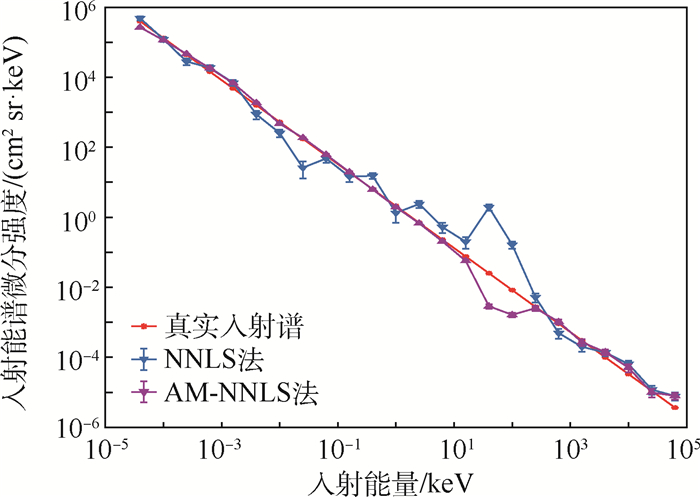
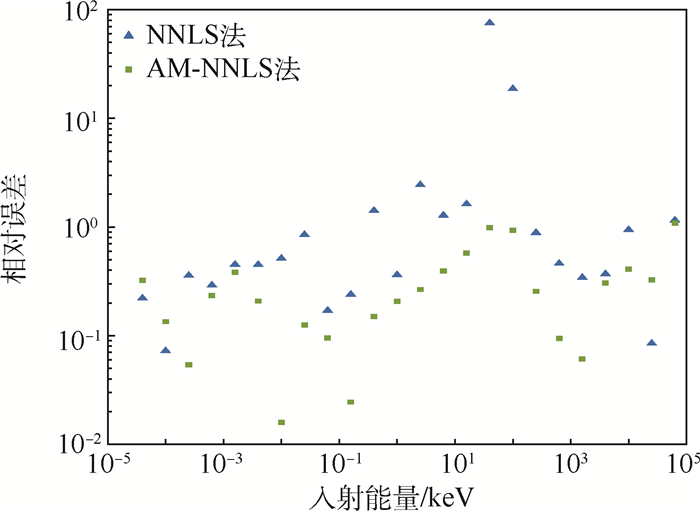
空间中子是影响航天器和航天员安全的重要辐射要素之一。优化中子探测器，提高测量效率，提升反演精度是中子测量的难点。中国空间站将搭载一种基于新型中子探测材料Cs2LiYCl6：Ce（CLYC）闪烁体的中子探测器，该探测器具有同时测量热中子和快中子，以及探测效率高等特点。针对该新型探测器的中子能谱反演，分析了不同能量中子在该探测器中的响应特点，分析了中子反演常用的概率迭代法和非负最小二乘（NNLS）法的优缺点，考虑到这2种方法在CLYC探测器反演应用中的不足，提出了基于增广矩阵的非负最小二乘（AM-NNLS）法。数值实验结果表明：AM-NNLS法具有反演运算效率高和反演相对误差小的特点，验证了所提方法的有效性。
- 空间站 /
- 蒙特卡罗仿真 /
- 中子探测器 /
- 最小二乘近似 /
- 能谱反演 /
- Cs2LiYCl6:Ce(CLYC)
Abstract:
Neutron is one of the important radiation factors that affect the safety of spacecraft and astronauts. It is difficult for neutron measurement to optimize the neutron detector, improve the measurement efficiency, and improve the inversion accuracy. A neutron detector based on a new type of neutron detection material Cs2LiYCl6:Ce (CLYC) scintillator will be installed on the space station in China. This detector has the characteristics of measuring thermal neutrons and fast neutrons simultaneously, and has high detection efficiency, etc. For the neutron spectrum inversion of this detector, the response characteristics of different energy neutrons in the detetor are analyzed, and the advantages and disadvantages of the probabilistic iterative method and Non-Negative Least Square (NNLS) method commonly used in neutron spectrum inversion are analyzed, considering the disadvantages of these two methods in the inversion application of CLYC detector, a Non-Negative Least Square method based on the Augmented Matrix (AM-NNLS) is proposed. The numerical experiment results show that the AM-NNLS method has the characteristics of high inversion operation efficiency and small inversion relative error, which verifies the effectiveness of the method.
- space station /
- Monte Carlo simulation /
- neutron detector /
- least squares approximations /
- spectrum inversion /
- Cs2LiYCl6:Ce (CLYC)

HTML全文

图 1 反符合结构

Figure 1. Anti-coincidence structure

下载: 全尺寸图片幻灯片

图 2 中子探测器的逻辑工作方式

Figure 2. Logic schematic diagram of neutron detector

下载: 全尺寸图片幻灯片

图 3 热中子以及5 MeV的单能中子在CLYC闪烁体中的沉积能谱

Figure 3. Deposited energy spectrum of thermal neutron and 5 MeV monoenergetic neutron in CLYC scintillator

下载: 全尺寸图片幻灯片

图 4 CLYC闪烁体中对热中子和快中子(0.025 eV~100 MeV)的响应函数

Figure 4. Response functions of thermal neutron and fast neutron (0.025 eV-100 MeV) in CLYC scintillator

下载: 全尺寸图片幻灯片

图 5 响应函数在每个能道的不确定度

Figure 5. Uncertainty of response function with different channels

下载: 全尺寸图片幻灯片

图 6 概率迭代法的反演步骤

Figure 6. Inversion steps of probabilistic iterative method

下载: 全尺寸图片幻灯片

图 7 基于概率迭代法和NNLS法的中子微分谱

Figure 7. Neutron differential spectrum based on probabilisticiterative method and NNLS

下载: 全尺寸图片幻灯片

图 8 NNLS法与AM-NNLS法的能谱对比

Figure 8. Comparative energy spectrum of non-negative least squares method and AM-NNLS

下载: 全尺寸图片幻灯片

图 9 相对误差

Figure 9. Relative error

下载: 全尺寸图片幻灯片

图 10 不同测量总计数时反演得到的能谱

Figure 10. Inverted energy spectra for different measurements

下载: 全尺寸图片幻灯片

图 11 测量总计数不同时2种反演方法得到的能谱与真实入射谱之间的相对误差

Figure 11. Relative error between energy spectrum obtained from two inversion methods and actual input spectrum when measured values are different

下载: 全尺寸图片幻灯片

表 1 中子与CLYC闪烁体反应过程^[15-16]

Table 1. Reaction of neutron with CLYC scintillator^[15-16]

反应	Q/MeV	能量区间
⁶Li+n→³H+ɑ	+4.78	热中子及快中子
³⁵Cl+n→³⁵S+P	+0.615	快中子

下载: 导出CSV

表 2 概率迭代法与AM-NNLS法反演能谱所需时间对比

Table 2. Time comparison between probabilistic iterative method and AM-NNLS for inversion of energy spectrum

测量总计数	耗时/s
测量总计数	概率迭代法	AM-NNLS
10²	138	5
10³	143	4
10⁴	156	5
10⁵	150	5

下载: 导出CSV

参考文献(25)

[1]	MOUNTFORD P J, TEMPERTON D H.Recommendations of the international commission on radiological protection(ICRP)1990[J].European Journal of Nuclear Medicine, 1992, 19(2):77-79. http://www.ncbi.nlm.nih.gov/pubmed/1563443
[2]	MAZUR J E, CRAIN W R, LOOPER M D, et al.New measurements of total ionizing dose in the lunar environment[J].Space Weather-The International Journal of Research & Applications, 2011, 9(7):1-12. http://ieeexplore.ieee.org/document/7766610/
[3]	KOSHIISHI H, MATSUMOTO H, CHISHIKI A, et al.Evaluation of the neutron radiation environment inside the International Space Station based on the bonner ball neutron detector experiment[J].Radiation Measurements, 2007, 42(9):1510-1520. doi: 10.1016/j.radmeas.2007.02.072
[4]	HASSLER D M, ZEITLIN C, WIMMER-SCHWEINGRUBER R F, et al.The radiation assessment detector (RAD) investigation[J].Space Science Reviews, 2012, 170(1-4):503-558. doi: 10.1007/s11214-012-9913-1
[5]	TANIGUCHI T, UEDA N, NAKAZAWA M, et al.Systematic study on spectral effects in the adjustment calculations using the NEUPAC-83 code[M].Berlin:Springer, 1985:685-691.
[6]	KOHLER J, EHRESMANN B, MARTIN C, et al.Inversion of neutron/gamma spectra from scintillator measurements[J].Nuclear Instruments and Methods in Physics Research B, 2011, 269:2641-2648. doi: 10.1016/j.nimb.2011.07.021
[7]	王冬, 何彬, 张全虎.用遗传算法求解中子能谱[J].原子能科学技术, 2010, 44(10):1270-1275. WANG D, HE B, ZHANG Q H.Unfolding neutron spectrum using genertic algorithm[J].Atomic Energy Science and Technology, 2010, 44(10):1270-1275(in Chinese).
[8]	杨鑫, 李润东, 刘汉刚, 等.基于概率迭代的NDP反演方法[J].计算物理, 2012, 29(6):891-900. doi: 10.3969/j.issn.1001-246X.2012.06.014 YANG X, LI R D, LIU H G, et al.An unfolding method of NDP based on probability iteration[J].Chinese Journal of Computational Physics, 2012, 29(6):891-900(in Chinese). doi: 10.3969/j.issn.1001-246X.2012.06.014
[9]	D'OLYMPIA N W, NATHAN W.Development of novel neutron and gamma-ray scintillators: Cs2LiYCl6: Ce and CeBr₃[D].Boston: University of Massachusetts, 2013: 8-40.
[10]	胡圣荣, 戴纳新.病态线性方程组的新解法:增广方程组法[J].华南农业大学学报, 2009, 30(1):119-121. HU S R, DAI N X.A novel method for solving Ⅲ-conditioned liner system:Augmented system method[J].Journal of South China Agricultural University, 2009, 30(1):119-121(in Chinese).
[11]	李肖.反符合探测杯在空间粒子探测中的应用[D].北京: 中国科学院, 2015: 5-23. LI X.The application of anti-coincidence detective cup technology in space particle detection[D].Beijing: University of Chinese Academy of Science, 2015: 5-23(in Chinese).
[12]	WHITNEY C M, SOUNDARA-PANDIAN L, JOHNSON E B, et al.Gamma-neutron imaging system utilizing pulse shape discrimination with CLYC[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2015, 784:346-351. doi: 10.1016/j.nima.2014.09.022
[13]	LEE D W, STONEHILL L C, KLIMENKO A, et al.Pulse-shape analysis of Cs2LiYCl6:Ce scintillator for neutron and gamma-ray discrimination[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2012, 664(1):1-5.
[14]	WANG Q B, TUO X G, DENG C, et al.Characterization of a Cs2LiYCl6:Ce³⁺ scintillator coupled with two silicon photomultiplier arrays of different sizes[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2019, 942:1-5. http://www.sciencedirect.com/science/article/pii/S0168900219309258
[15]	D'OLYMPIA N W, CHOWDHURY P, LISTER C J, et al.Pulse-shape analysis of CLYC for thermal neutrons, fast neutrons, and gamma-rays[J].Nuclear Instruments and Methods in Physics Research Section A:Accereators, Spectrometers, Detectors and Associated Equipment, 2013, 714:121-127. http://www.sciencedirect.com/science/article/pii/S0168900213002349
[16]	BROWN D, CHADWICK M B, CAPOTE R, et al.ENDF/B-Ⅷ.0:The 8th major release of the nuclear reaction data library with CIELO-project cross sections, new stantards and thermal scattering data[J].Nuclear Data Sheets, 2018, 148(2):1-142.
[17]	AGOSTINELLI S, ALLISON J, AMAKO K, et al.GEANT4-A simulation toolkit[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2003, 506(3):250-303.
[18]	ZHANG S Y, ZHANG X G, WANG C Q, et al.The geometric factor of high energy protons detector on FY-3 satellite[J].Science China Earth Sciences, 2014, 57(10):2558-2566. doi: 10.1007/s11430-014-4853-0
[19]	KHARYTONOV A, BÖHM, E, WIMMER-SCHWEINGRUBER R F.Regularization methods used in error analysis of solar particle spectra measured on SOHO/EPHIN[J].Astronomy & Astrophysics, 2009, 495(2):663-675.
[20]	GUO J N, BANJAC S, ROSTEL L, et al.Implementation and validation of the GEANT4/AtRIS code to model the radiation environment at Mars[J].Journal of Space Weather and Space Climate, 2019, 9(3):1-30. http://arxiv.org/abs/1901.01787
[21]	NOWAK R D, KOLACZYK E D.A statistical multiscale framework for Poisson inverse problems[J].IEEE Transactions on Information Theory, 2000, 46(5):1811-1825. doi: 10.1109/18.857793
[22]	WILLIAM H P, BRIAN P F, SAUL A, et al.Numerical recipes:The art of scientific computing[M].Cambridge:Cambridge University Press, 2007:809-816.
[23]	LAWSON C L, HANSON R J.Solving least squares problems[M].Philadelphia:Society for lndustrial and Applied Mathematics, 1987:1-5.
[24]	BÖHM E, KHARYTONOV A, WIMMER-SCHWEINGRUBER R F.Solar energetic particle spectra from the SOHO-EPHIN sensor by application of regularization methods[J].Astronomy & Astrophysics, 2007, 473(2):673-682.
[25]	MORALE J L, NOCEDAL J.Remark on 'algorithm 778:L-BFGS-B:Fortran subroutines for large-scale bound constrained optimization'[J].ACM Transactions on Mathematical Software, 2011, 38(1):1-4.