改进粒子群优化的卫星导航选星算法

王尔申; 孙彩苗; 黄煜峰; 李轩; 别玉霞; 曲萍萍

doi:10.13700/j.bh.1001-5965.2019.0644

改进粒子群优化的卫星导航选星算法

doi: 10.13700/j.bh.1001-5965.2019.0644

王尔申^{1, 2, ,},
孙彩苗¹,
黄煜峰¹,
李轩¹,
别玉霞¹,
曲萍萍¹

1.
沈阳航空航天大学电子信息工程学院, 沈阳 110136
2.
沈阳航空航天大学辽宁省通用航空重点实验室, 沈阳 110136

基金项目:

国家自然科学基金 61571309

国家自然科学基金 61901284

辽宁省重点研发计划 2020JH2/10100045

辽宁省"百千万人才工程" 04021407

辽宁省自然科学基金 2019-MS-251

辽宁省教育厅科研项目 L201705

辽宁省教育厅科研项目 L201716

辽宁省高等学校优秀人才支持计划 LR2016069

辽宁省"兴辽英才计划" XLYC1907022

沈阳市高层次创新人才计划 RC190030

详细信息

作者简介:
王尔申男, 博士, 教授。主要研究方向:卫星导航、航空电子技术

通讯作者:
王尔申, E-mail: wanges_2016@126.com

中图分类号: V241.6;TN967.1
计量
- 文章访问数: 940
- HTML全文浏览量: 98
- PDF下载量: 252
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-24
- 录用日期: 2020-01-11
- 网络出版日期: 2021-01-20

Satellite navigation satellite selection algorithm based on improved particle swarm optimization

1.
College of Electronic and Information Engineering, Shenyang Aerospace University, Shenyang 110136, China
2.
Liaoning General Aviation Key Laboratory, Shenyang Aerospace University, Shenyang 110136, China

Funds:

National Natural Science Foundation of China 61571309

National Natural Science Foundation of China 61901284

Key R & D Program of Liaoning Province 2020JH2/10100045

Liaoning "BaiQianWan Talents Program" 04021407

Natural Science Foundation of Liaoning Province 2019-MS-251

Scientific Research Project of Liaoning Provincial Department of Education L201705

Scientific Research Project of Liaoning Provincial Department of Education L201716

Program for Liaoning Excellent Talents in University LR2016069

Talent Project of Revitalization Liaoning XLYC1907022

High-Level Innovation Talent Project of Shenyang RC190030

More Information

Corresponding author: WANG Ershen, E-mail:wanges_2016@126.com

摘要

摘要:
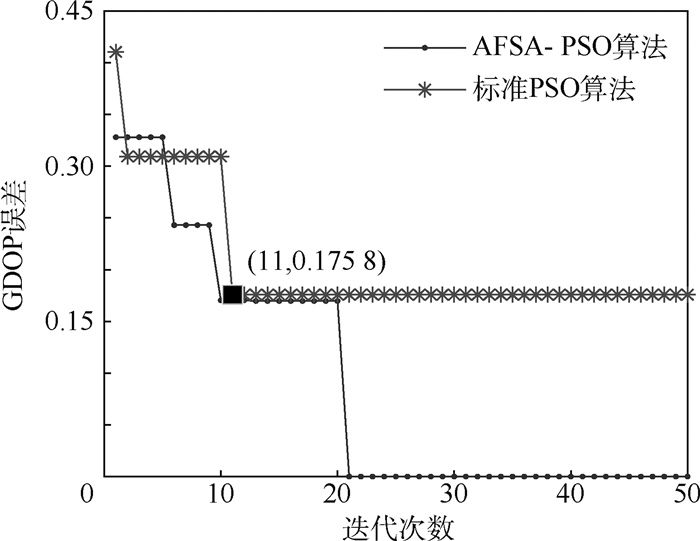
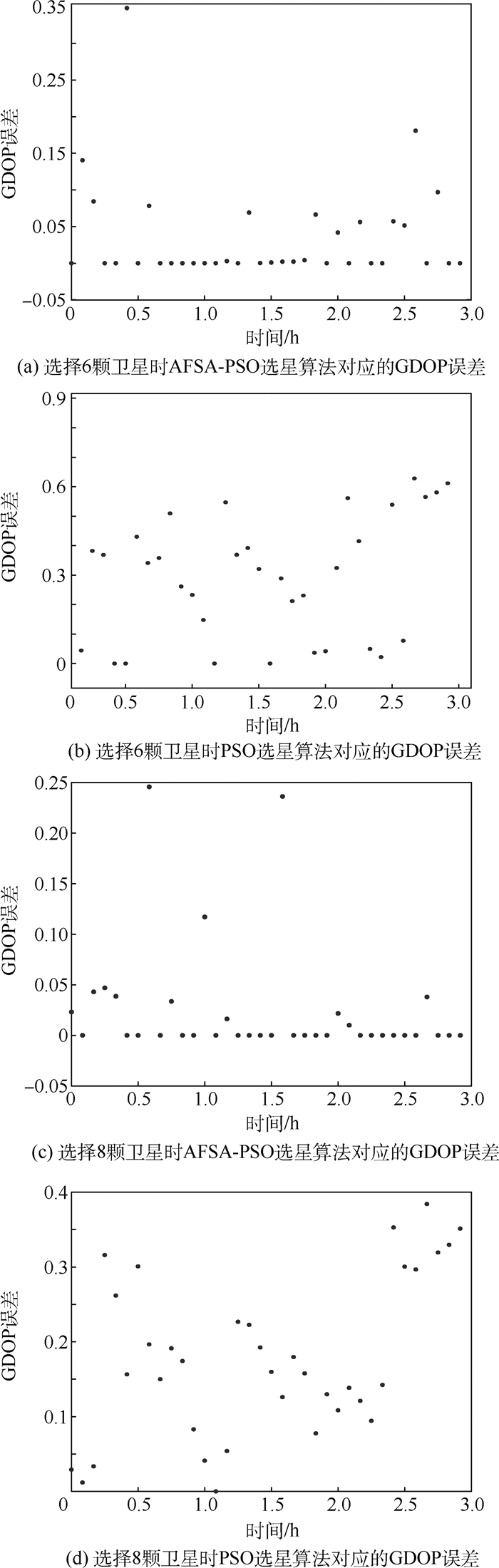
为提高选星算法的性能，提出一种基于人工鱼群算法的粒子群优化（PSO）选星算法。该算法利用人工鱼群算法良好的全局收敛特性，克服了粒子群优化算法易陷入局部最优的缺点。将每种卫星组合看作空间中的一个粒子，选取几何精度因子（GDOP）作为适应度函数。利用所提算法更新粒子自身位置，优化卫星组合与几何精度因子。利用实际数据对所提算法进行验证和对比，结果表明：改进的选星算法在保障选星效率的同时，选星结果的准确性优于标准的粒子群优化选星算法。
- 卫星导航 /
- 选星 /
- 几何精度因子(GDOP) /
- 粒子群优化(PSO)算法 /
- 人工鱼群算法
Abstract:
In order to improve the performance of satellite selection algorithm, the Particle Swarm Optimization (PSO) satellite selection algorithm based on artificial fish swarm algorithm is proposed. Using the global convergence characteristics of artificial fish swarm algorithm, the algorithm can overcome the shortcomings of PSO algorithm that is easy to fall into local optimum. The improved algorithm treats each satellite combination as a particle in space, and the Geometric Dilution of Precision (GDOP) is chosen as the fitness function. The particle updates its position based on the optimization principle of the particle swarm optimization algorithm and artificial fish swarm algorithm, and the optimal satellite combination and GDOP value are obtained. The algorithms are verified and compared with real data, and the results show that the improved satellite selection algorithm not only guarantees the efficiency of the satellite selection, but also the accuracy of the satellite selection result is better than that of the satellite selection algorithm based on the PSO.
- satellite navigation /
- satellite selection /
- Geometric Dilution of Precision (GDOP) /
- Particle Swarm Optimization (PSO) algorithm /
- artificial fish swarm algorithm

HTML全文

图 1 可见卫星数及对应的最小GDOP值

Figure 1. Visible number of satellites and corresponding min-GDOP

下载: 全尺寸图片幻灯片

图 2 单次选星GDOP误差变化

Figure 2. GDOP error change of single satellite selection

下载: 全尺寸图片幻灯片

图 3 AFSA-PSO算法与PSO算法的GDOP误差

Figure 3. GDOP error in AFSA-PSO and PSO algorithms

下载: 全尺寸图片幻灯片

表 1 视野对算法性能的影响

Table 1. Effect of visual field on algorithm performance

视野	最大GDOP误差	平均GDOP误差	选星耗时/s
2	0.112 5	0.065 21	2.451 830
4	0.137 5	0.057 34	2.691 055
6	0.100 5	0.051 91	2.869 438
8	0.107 5	0.030 03	2.938 141
10	0.096 4	0.027 48	2.969 203

下载: 导出CSV

表 2 移动步长对算法性能的影响

Table 2. Effect of step length on algorithm performance

移动步长	最大GDOP误差	平均GDOP误差	选星耗时/s
6	0.289 2	0.093 55	3.291 174
8	0.168 6	0.055 69	3.018 298
10	0.107 5	0.047 54	2.855 520
12	0.113 5	0.087 41	2.866 246
14	0.119 6	0.094 40	2.965 653

下载: 导出CSV

表 3 拥挤度因子对算法性能的影响

Table 3. Effect of crowding factor on algorithm performance

拥挤度因子	最大GDOP误差	平均GDOP误差	选星耗时/s
0.2	0.214 9	0.123 94	3.153 434
0.4	0.107 5	0.067 93	2.240 370
0.6	0.129 0	0.095 77	2.083 249
0.8	0.119 6	0.080 65	2.022 105
1	0.113 5	0.097 68	3.082 750

下载: 导出CSV

表 4 不同选星算法单次选星耗时

Table 4. Single satellite selection time of different satellie selection algorithms

算法	单次选星耗时/s	GDOP值	最佳卫星组合
遍历法	4.902 163	2.251 028	9 21 27 31 38 39
AFSA-PSO	2.502 947	2.251 028	9 21 27 31 38 39
PSO	1.695 711	2.358 500	9 21 27 39 38 37

下载: 导出CSV

参考文献(16)

[1]	吴丹.GNSS观测数据预处理及质量评估[D].西安: 长安大学, 2015. WU D.GNSS observation data preprocessing and quality assessment[D].Xi'an: Chang'an University, 2015(in Chinese).
[2]	WANG E S, YANG D, WANG C Y, et al.Optimized fault detection algorithm aided by BDS baseband signal for train positioning[J].Chinese Journal of Electronics, 2020, 29(1):34-40. doi: 10.1049/cje.2019.09.004
[3]	BO X, SHAO B.Satellite selection algorithm for combined GPS-Galileo navigation receiver[C]//International Conference on Autonomous Robots and Agents.Piscataway: IEEE Press, 2009: 149-154.
[4]	PHATAK M S.Recursive method for optimum GPS satellite selection[J].IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2):751-754. doi: 10.1109/7.937488
[5]	SONG J C, XUE G X, KANG Y A.A novel method for optimum global positioning system satellite selection based on a modified genetic algorithm[J].PloS One, 2016, 11(3):e0150005. doi: 10.1371/journal.pone.0150005
[6]	胡思华, 张显云, 李婷, 等.顾及观测质量的多系统融合PPP三维凸包选星算法[J].大地测量与地球动力学, 2019, 39(3):269-272. https://www.cnki.com.cn/Article/CJFDTOTAL-DKXB201903012.htm HU S H, ZHANG X Y, LI T, et al.Three-dimensional convex hull satellites selection algorithm:Considering the quality of observation[J].Journal of Geodesy and Geodynamics, 2019, 39(3):269-272(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DKXB201903012.htm
[7]	LIU X, ZHANG S B, ZHANG Q Z, et al.A fast satellite selection algorithm with floating high cut-off elevation angle based on ADOP for instantaneous multi-GNSS single-frequency relative positioning[J].Advances in Space Research, 2019, 63(3):1234-1252. doi: 10.1016/j.asr.2018.10.032
[8]	霍国平, 缪玲娟, 高志峰.基于3星子集的GPS快速选星算法[J].宇航学报, 2014, 35(5):574-580. doi: 10.3873/j.issn.1000-1328.2014.05.011 HUO G P, MIAO L J, GAO Z F.GPS fast constellation selection based on 3-SAT subset[J].Journal of Astronautics, 2014, 35(5):574-580(in Chinese). doi: 10.3873/j.issn.1000-1328.2014.05.011
[9]	EBERHART R C, KENNEDY J.A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Piscataway: IEEE Press, 1995: 39-43.
[10]	王雪莹, 安玮, 李骏.天基光学短弧观测约束域的粒子群优化定轨方法[J].国防科技大学学报, 2014, 36(6):146-151. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201406026.htm WANG X Y, AN W, LI J.An orbit-determination method with particle swarm optimization using space-based optical short-arc observation in admissible region[J].Journal of National University of Defense Technology, 2014, 36(6):146-151(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201406026.htm
[11]	WEI P, LI Y, ZHANG Z, et al.An optimization method for intrusion detection classification model based on deep belief network[J].IEEE Access, 2019, 7:87593-87605. doi: 10.1109/ACCESS.2019.2925828
[12]	钊守国, 周长林, 梁臻鹤, 等.一种基于群体行为动力学的粒子群优化算法[J].信息工程大学学报, 2017, 18(3):299-304. doi: 10.3969/j.issn.1671-0673.2017.03.009 ZHAO S G, ZHOU C L, LIANG Z H, et al.Particle swarm optimization algorithm based on collective behavior dynamics[J].Journal of Information Engineering University, 2017, 18(3):299-304(in Chinese). doi: 10.3969/j.issn.1671-0673.2017.03.009
[13]	席亮, 王勇, 张凤斌.基于自适应人工鱼群FCM的异常检测算法[J].计算机研究与发展, 2019, 56(5):1048-1059. https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ201905015.htm XI L, WANG Y, ZHANG F B.Anomaly detection algorithm based on FCM with adaptive artificial fish-swarm[J].Journal of Computer Research and Development, 2019, 56(5):1048-1059(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ201905015.htm
[14]	HE J, JIN X, XIE S Y, et al.Multi-body dynamics modeling and TMD optimization based on the improved AFSA for floating wind turbines[J].Renewable Energy, 2019, 141:305-321. doi: 10.1016/j.renene.2019.04.005
[15]	EBERHART R C, SHI Y H.Particle swarm optimization: Developments, applications and resources[C]//Proceedings of the 2001 Congress on Evolutionary Computation.Piscataway: IEEE Press, 2002: 81-86.
[16]	王尔申, 贾超颖, 曲萍萍, 等.基于混沌粒子群优化的北斗/GPS组合导航选星算法[J].北京航空航天大学学报, 2019, 45(2):259-265. doi: 10.13700/j.bh.1001-5965.2018.0281 WANG E S, JIA C Y, QU P P, et al.BDS/GPS integrated navigation satellite selection algorithm based on chaos particle swarm optimization[J].Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2):259-265(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0281