System identification of a 2-DOF wing section with freeplay nonlinearity
-
摘要:
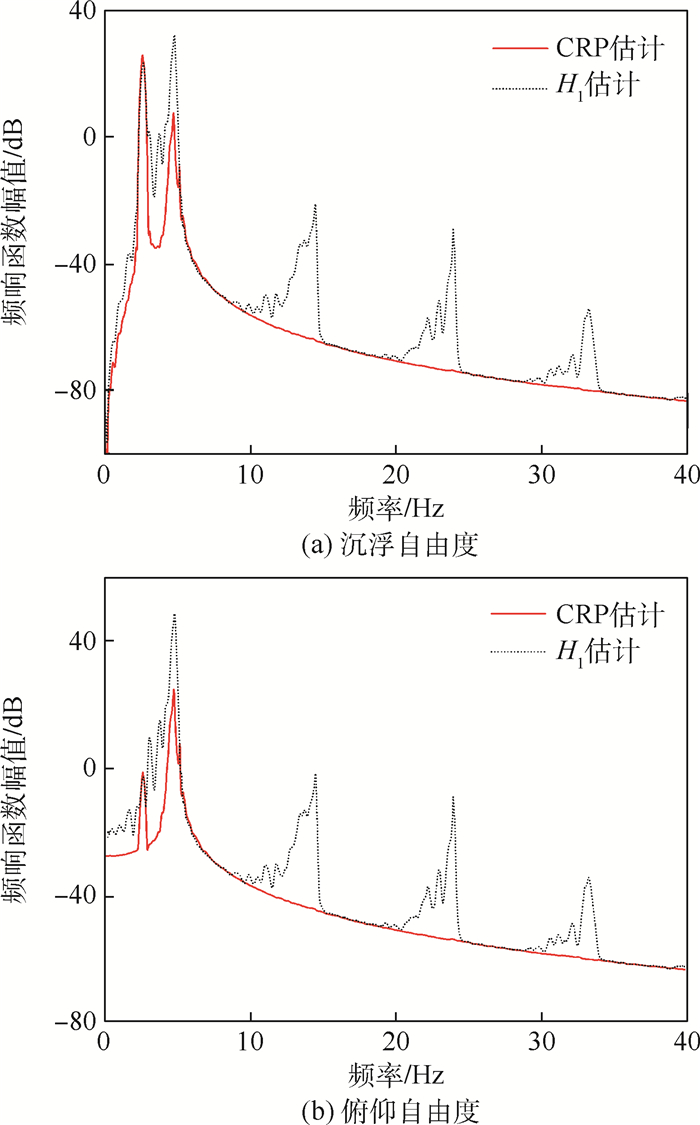
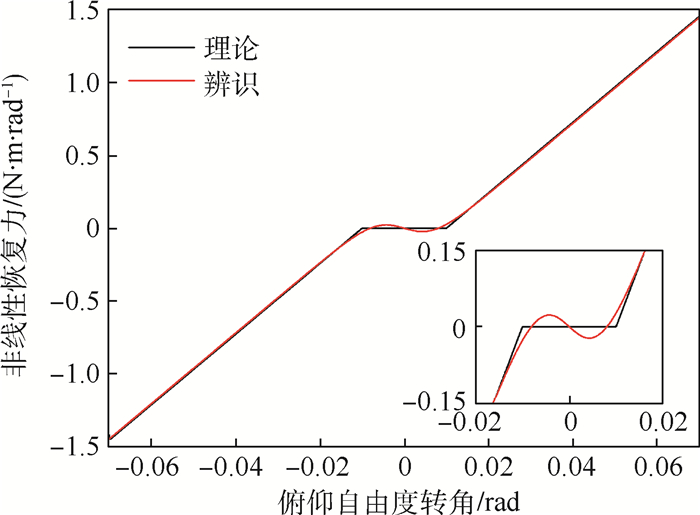
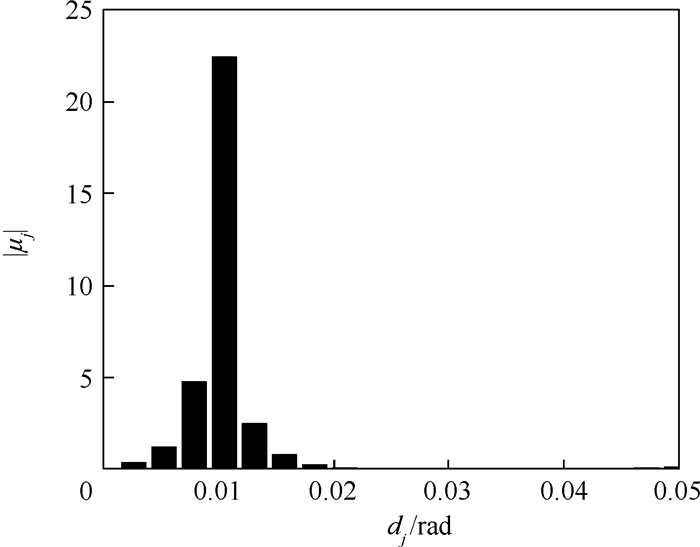
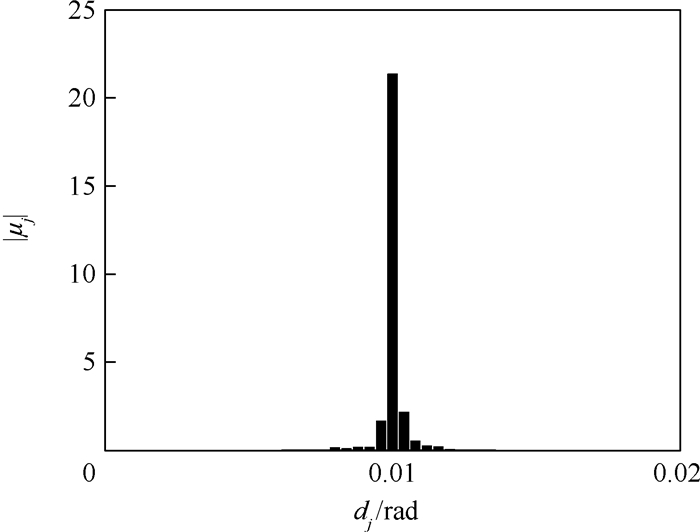
在实际包含间隙非线性的复杂结构中，由于间隙不易或无法测量，难以建立准确描述结构特性的动力学模型；即使间隙得到准确测量，也难以获得结构的标称线性系统的模态参数。为此，利用条件逆谱法和时域非线性子空间法，通过非线性系统辨识获得间隙非线性系数，同时获得非线性结构的标称线性系统的频响函数。以一个包含间隙非线性的二元翼段为例，通过数值方法模拟该二元翼段的地面振动试验，利用条件逆谱法和时域非线性子空间法开展该结构的非线性系统辨识。结果表明：两种方法均可准确地辨识结构的标称线性系统，条件逆谱法利用光滑函数近似，时域非线性子空间法利用多个分段线性函数重构，辨识得到间隙非线性系数。
Abstract:On one hand, it is difficult to establish an accurate dynamical model description reflecting structural characteristics of a real-world complex structure with freeplay nonlinearity because of the inconvenience or impossibility of measuring the gap. On the other hand, even though the freeplay has been estimated, the modal parameters of the nominal linear system of the structure are still out of reach. Therefore, in this paper, nonlinear system identification was performed by the usage of conditioned reverse path method and time-domain nonlinear subspace identification method to obtain the parameters of freeplay nonlinearity as well as the frequency response function of the nominal linear system of the nonlinear structure. A 2-DOF wing section was chosen as a demonstration, on which the numerical experiments of ground vibration tests were performed. Nonlinear system identification was carried out by applying the conditioned reverse path method and time-domain nonlinear subspace identification method. Consequently, the nominal linear system can be accurately estimated by both methods, and the identified parameters of freeplay nonlinearity can also be obtained by smooth function approximation in conditioned reverse path method and by reconstruction via a series of piecewise linear functions in time-domain nonlinear subspace identification method.
-
图 9 低激励水平与高激励水平的频响函数曲线对比
Figure 9. Comparison of FRFs under low excitation level and high excitation level
图 14 区间[0, max(α)]内的非线性系数分布
Figure 14. Nonlinear parameter distribution in the interval [0, max(α)]
图 15 区间[0.008, 0.012]rad内的非线性系数分布
Figure 15. Nonlinear parameter distribution in the interval [0.008, 0.012]rad
图 16 辨识得到的非线性二元翼段ULS的频响函数曲线
Figure 16. Identified FRF of ULS of nonlinear 2-DOF wing section
图 17 时域非线性子空间法辨识的非线性恢复力曲线
Figure 17. Nonlinear restoring force identified by TNSI method
图 18 辨识得到的非线性二元翼段OLS的频响函数曲线
Figure 18. Identified FRF of OLS of nonlinear 2-DOF wing section
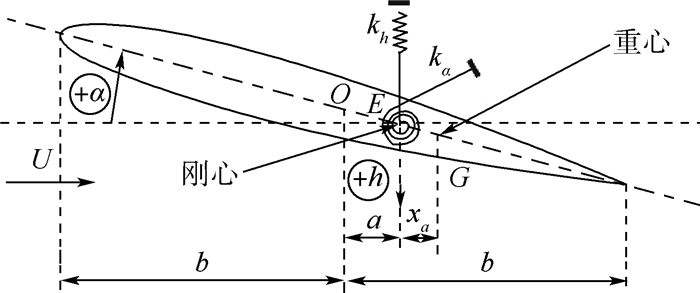
表 1 二元翼段结构基本参数
Table 1. Main structural parameters of 2-DOF wing section
参数 数值 半弦长b/m 0.1 刚心与中心相对距离a -0.2 质量m/kg 2.9 重心与刚心距离xa/m 0.01 静矩Sα/(kg·m) 0.029 转动惯量Iα/(kg·m2) 0.024 
下载: 导出CSV
表 2 激励水平与对应的随机力RMS值
Table 2. Excitation levels and corresponding RMS value of random excitation force
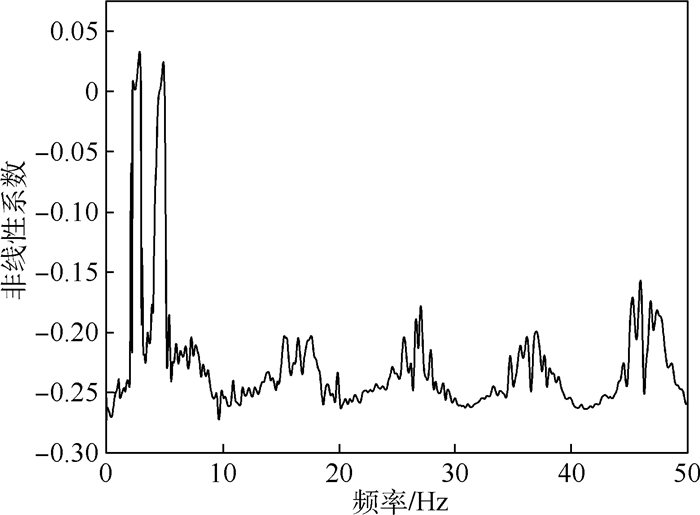
激励水平 随机力RMS/N 1 0.004 8 2 0.011 8 3 0.022 6 4 0.048 6 5 0.069 0 6 0.114 4 7 0.182 5 8 0.230 8 9 0.486 0 10 0.729 6 11 1.100 0 12 1.997 4 13 2.215 9 14 2.767 9 15 3.722 0 16 4.970 4 17 7.373 1 18 11.610 5 19 25.501 0
下载: 导出CSV
表 3 不同激励水平下辨识的非线性系数
Table 3. Identified nonlinear coefficient under different excitation levels
随机力RMS/(N·m) 非线性系数 0.048 6 -0.250 8 0.069 0 -0.253 8 0.230 8 -0.250 5 0.486 0 -0.244 0
下载: 导出CSV
表 4 条件逆谱法和时域非线性子空间法属性对比
Table 4. Property comparison between CRP and TNSI
属性 条件逆谱法 时域非线性子空间法 域 频域 时域 多自由度 是 是 多种非线性 是 是 迭代计算 是 否 数据 稳态数据 任意数据 数据前处理 离散傅里叶变换 否 间隙描述 函数近似 多间隙重构 稳态图 是 是 计算量 低 中等 ULS辨识精度 高 高 OLS辨识精度 高 高 间隙辨识精度 间隙边界：一般
刚度辨识：高间隙边界：高
刚度辨识：高
下载: 导出CSV
-
[1] 杨宁.间隙非线性结构的气动弹性建模与分析方法研究[D].北京: 北京航空航天大学, 2014: 1-2.YANG N.Studies on aeroelastic modeling and analysis methods of structures with freeplay nonlinearity[D].Beijing: Beihang University, 2014: 1-2(in Chinese). [2] DOWELL E H, EDWARDS J, STRGANAC T W.Nonlinear aeroelasticity[J].Journal of Aircraft, 2003, 40(5):857-874. doi: 10.2514/2.6876 [3] SHETA F, HARRAND V J, THOMPSON D E, et al.Computation and experimental investigation of limit cycle oscillations of nonlinear aeroelastic systems[J].Journal of Aircraft, 2002, 39(1):133-141. doi: 10.2514/2.2907 [4] BAE J S, YANG S M, LEE I.Linear and nonlinear aeroelastic analysis of fighter-type wing with control surface[J].Journal of Aircraft, 2002, 39(4):697-708. doi: 10.2514/2.2984 [5] 李志涛, 韩景龙.间隙非线性气动弹性系统的辨识[J].航空学报, 2012, 33(11):2002-2009. http://www.cnki.com.cn/Article/CJFDTotal-HKXB201211008.htmLI Z T, HAN J L.Identification of a nonlinear aeroelastic system with freeplay[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(11):2002-2009(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-HKXB201211008.htm [6] KERSCHEN G, WORDEN K, VAKAKIS A F, et al.Past, present and future of nonlinear system identification in structural dynamics[J].Mechanical Systems and Signal Processing, 2006, 20(3):505-592. doi: 10.1016/j.ymssp.2005.04.008 [7] KUKREJA S L, BRENNER M.Nonlinear black-box modeling of aeroelastic systems using structure detection:Application to F/A-18 data[J].Journal of Guidance, Control, and Dynamics, 2007, 30(2):557-564. doi: 10.2514/1.20835 [8] POPESCU C A, WONG S Y, LEE B H K.An expert system for predicting nonlinear aeroelastic behavior of an airfoil[J].Journal of Sound and Vibration, 2009, 319(5):1312-1329. doi: 10.1016/j.jsv.2008.06.035 [9] WU Z G, YANG N, YANG C.Identification of nonlinear multi-degree-of freedom structures based on Hilbert transformation[J].Science China Physics, Mechanics & Astronomy, 2014, 57(9):1725-1736. doi: 10.1007/s11433-013-5218-y [10] WU Z G, YANG N, YANG C.Identification of nonlinear structures by the conditioned reverse path method[J].Journal of Aircraft, 2015, 52(2):373-386. doi: 10.2514/1.C032424 [11] CRAWLEY E F, AUBERT A C.Identification of nonlinear structural elements by force-state mapping[J].AIAA Journal, 1986, 24(1):155-162. doi: 10.2514/3.9236 [12] RICHARDS C M, SINGH R.Identification of multi-degree-of-freedom non-linear systems under random excitations by the "reverse path" spectral method[J].Journal of Sound and Vibration, 1998, 213(4):673-708. doi: 10.1006/jsvi.1998.1522 [13] RICE H J, FITZPATRICK J A.A procedure for the identification of linear and non-linear multi-degree-of-freedom systems[J].Journal of Sound and Vibration, 1991, 149(3):397-411. doi: 10.1016/0022-460X(91)90444-O [14] RICHARDS C M, SINGH R.Feasibility of identifying non-linear vibratory systems consisting of unknown polynomial forms[J].Journal of Sound and Vibration, 1999, 220(3):413-450. doi: 10.1006/jsvi.1998.1918 [15] MARCHESIELLO S, GARIBALDI L.Subspace-based identification of nonlinear structures[J].Shock and Vibration, 2008, 15(3-4):345-354. doi: 10.1155/2008/873183 [16] MARCHESIELLO S, GARIBALDI L.A time domain approach for identifying nonlinear vibrating structures by subspace methods[J].Mechanical Systems and Signal Processing, 2008, 22(1):81-101. doi: 10.1016/j.ymssp.2007.04.002 [17] LEE B H K, PRICE S J, WONG Y S.Nonlinear aeroelastic analysis of airfoils:Bifurcation and chaos[J].Progress in Aerospace Sciences, 1999, 35(3):205-334. doi: 10.1016/S0376-0421(98)00015-3 [18] 陈衍茂, 刘济科, 孟光.二元机翼非线性颤振系统的若干分析方法[J].振动与冲击, 2011, 30(3):129-134. doi: 10.3969/j.issn.1000-3835.2011.03.026CHEN Y M, LIU J K, MENG G.Some analysis methods for nonlinear flutter of a two-dimensional airfoil:A review[J].Journal of Vibration and Shock, 2011, 30(3):129-134(in Chinese). doi: 10.3969/j.issn.1000-3835.2011.03.026 [19] 杨智春, 田玮, 谷迎松, 等.带线性的机翼气动弹性问题研究进展[J].航空学报, 2016, 37(7):2013-2044. doi: 10.7527/S1000-6893.2016.0140YANG Z C, TIAN W, GU Y S, et al.Advance in the study on wing aeroelasticity with concentrated nonlinearity[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(7):2013-2044(in Chinese). doi: 10.7527/S1000-6893.2016.0140 [20] 杨超.飞行器气动弹性原理[M].2版.北京:北京航空航天大学出版社, 2016:76-79.YANG C.Principal of aircraft aeroelasticity[M].2nd ed.Beijing:Beihang University Press, 2016:76-79(in Chinese). [21] DIMITRIADIS G.Introduction to nonlinear aeroelasticity[M].Chichester:John Wiley & Sons, Inc., 2017:264-269. [22] PEETERS B, AUWERAER H V D, GUILLAUME P.The PolyMAX frequency domain method:A new standard for modal parameter estimation[J].Shock and Vibration, 2004, 11:395-409. doi: 10.1155/2004/523692 -
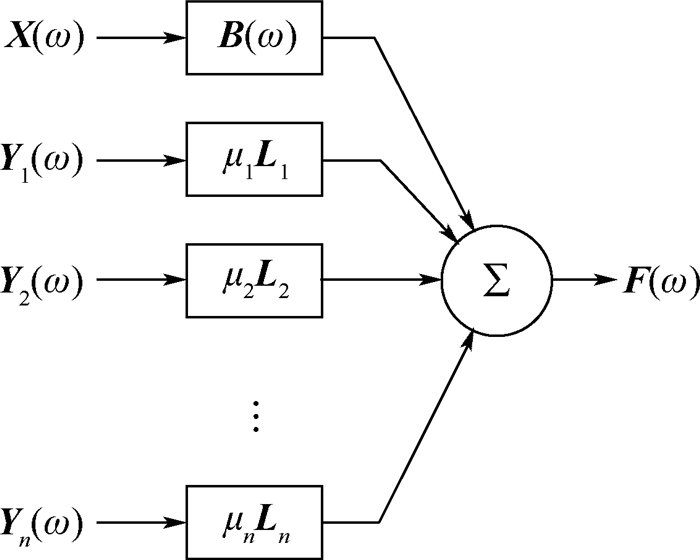
下载:
点击查看大图
计量
- 文章访问数: 496
- HTML全文浏览量: 64
- PDF下载量: 68
- 被引次数: 0
