不确定理论下竞争失效系统的可靠性分析

师海燕; 魏淳; 温艳清; 张志强; 刘宝亮

doi:10.13700/j.bh.1001-5965.2019.0656

不确定理论下竞争失效系统的可靠性分析

doi: 10.13700/j.bh.1001-5965.2019.0656

1.
山西大同大学数学与统计学院, 大同 037009
2.
山西大同大学物理与电子科学学院, 大同 037009

基金项目:

国家自然科学基金 71601101

山西省高等学校科技创新项目 2019L0738

详细信息

作者简介:
师海燕女, 硕士, 讲师。主要研究方向:可靠性理论及其应用

温艳清女, 博士, 副教授。主要研究方向:可靠性理论及其应用

通讯作者:
温艳清

中图分类号: O213;O211.62
计量
- 文章访问数: 1012
- HTML全文浏览量: 233
- PDF下载量: 245
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-31
- 录用日期: 2020-02-29
- 网络出版日期: 2021-01-20

Reliability analysis for systems subject to competing failure processes based on uncertainty theory

1.
College of Mathematics and Statistics Science, Shanxi Datong University, Datong 037009, China
2.
College of Physics and Electronics Science, Shanxi Datong University, Datong 037009, China

Funds:

National Natural Science Foundation of China 71601101

Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi 2019L0738

摘要

摘要:
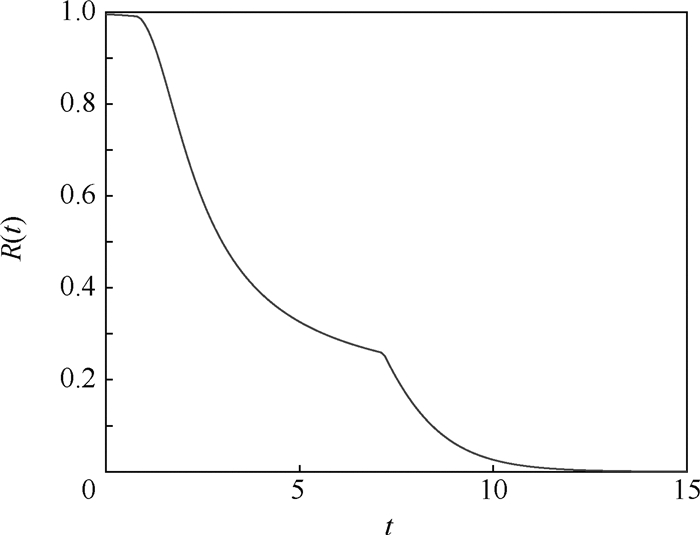
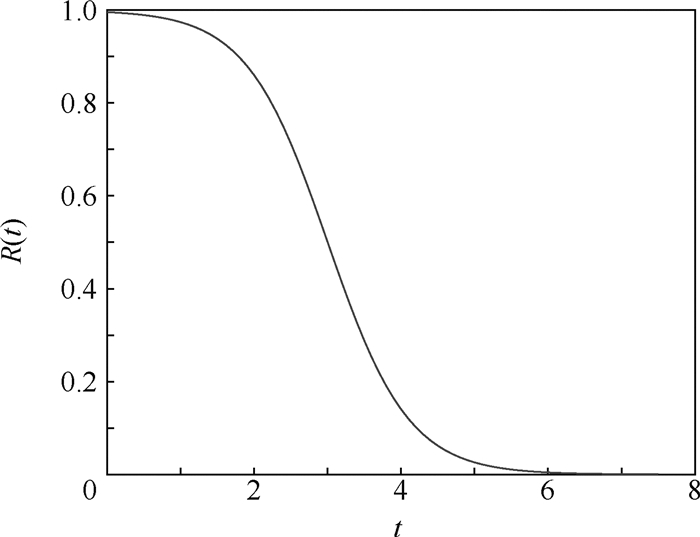
针对有新研发产品，故障数据较少的复杂系统，提出了不确定环境下自然退化和外部冲击相互独立的竞争失效模型。考虑了系统同时遭受自然退化和外部冲击，连续的自然退化用一个不确定过程刻画，冲击到达的时间间隔和每次冲击对系统造成的损坏量分别用2个不同的不确定变量来刻画。运用不确定理论，分别在极端冲击模型、累积冲击模型、δ冲击模型下，研究了系统的确信可靠度，结果表明：在有新研发的产品、故障数据较少的复杂系统，用不确定理论的方法来描述模型更合适，并通过数值分析显示了模型的有效性。
- 竞争失效过程 /
- 不确定理论 /
- 不确定变量 /
- 不确定分布 /
- 可靠性分析
Abstract:
For complex systems with newly developed products and less failure data, a competitive failure model in which natural degradation and external shocks are independent of each other in an uncertain environment is proposed. Considering that the system suffers from natural degradation and external shocks at the same time, the continuous natural degradation is described by an uncertain process, and the time interval of the shock arrival and the damage to the system caused by each shock are described by two different uncertain variables. Using the uncertainty theory, the system belief reliability is studied under the extreme shock model, cumulative shock model, and δ shock model. The results show that in the case of newly developed products and complex systems with less failure data, the method of uncertainty theory is more appropriate to describe the model, and numerical analysis shows the effectiveness of the model.
- competing failure processes /
- uncertainty theory /
- uncertain variable /
- uncertain distribution /
- reliability analysis

HTML全文

图 1 极端冲击模型的确信可靠度R(t)

Figure 1. Belief reliability R(t) of extreme shock model

下载: 全尺寸图片幻灯片

图 2 累积冲击模型的确信可靠度R(t)

Figure 2. Belief reliability R(t) of cumulative shock model

下载: 全尺寸图片幻灯片

图 3 δ冲击模型的确信可靠度R(t)

Figure 3. Belief reliability R(t) of δ shock model

下载: 全尺寸图片幻灯片

表 1 模型的参数值

Table 1. Model parameter values

参数	数值	来源
σ	1	假设
σ₁	1	假设
σ₂	1	假设
e	1	假设
e₁	3	假设
e₂	2.7	假设
H	3	Hao和Yang^[23]
D	10	假设
δ	0.1	Wang等^[24]

下载: 导出CSV

参考文献(24)

[1]	KLUTKE G A, YANG Y.The availability of inspected systems subject to shocks and graceful degradation[J].IEEE Transactions on Reliability, 2002, 51(3):371-374. doi: 10.1109/TR.2002.802891
[2]	WEI H, RONALD G A.Generalized SSI reliability model considering stochastic loading and strength aging degradation[J].IEEE Transactions on Reliability, 2004, 53(1):77-82. doi: 10.1109/TR.2004.823847
[3]	LI W J, PHAM H.An inspection-maintenance model for systems with multiple competing processes[J].IEEE Transaction on Reliability, 2005, 54(2):318-327. doi: 10.1109/TR.2005.847264
[4]	WANG Z L, DU L, HUANG H Z.Reliability modeling for dependent competitive failure processes[C]//Annual Reliability and Maintainability Symposium.Piscataway: IEEE Press, 2008: 279-283.
[5]	PENG H, FENG Q M, COITD W.Reliability and maintenance modeling for systems subject to multiple dependent competing failure processes[J].IIE Transactions, 2011, 43(1):12-22.
[6]	ZADEH L A.Fuzzy sets[J].Information and Control, 1965, 8:338-353. doi: 10.1016/S0019-9958(65)90241-X
[7]	潘刚, 尚朝轩, 梁玉英, 等.考虑认知不确定的雷达功率放大系统可靠性评估[J].北京航空航天大学学报, 2016, 42(6):1185-1194. doi: 10.13700/j.bh.1001-5965.2015.0390 PAN G, SHANG C X, LIANG Y Y, et al.Reliability evaluation of radar power amplification system considering epistemic uncertainty[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(6):1185-1194(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0390
[8]	武月琴, 周泓.N中连续取k好可修系统的模糊可靠性[J].北京航空航天大学学报, 2009, 35(1):52-55. doi: 10.3969/j.issn.1008-2204.2009.01.011 WU Y Q, ZHOU H.Fuzzy reliability of repairable consecutive k-out-of-n system[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(1):52-55(in Chinese). doi: 10.3969/j.issn.1008-2204.2009.01.011
[9]	LIU B D.Why is there a need for uncertainty theory [J].Journal of Uncertain System, 2012, 6(1):3-10. http://www.researchgate.net/publication/228449921_Why_is_there_a_need_for_uncertainty_theory
[10]	LIU B D.Uncertainty theory[M].2rd ed.Berlin:Springer, 2007:205-228.
[11]	LIU B D.Fuzzy process, hybrid process and uncertain process[J].Journal of Uncertain System, 2008, 2(1):3-16.
[12]	LIU B D.Some research problems in uncertainty theory[J].Journal of Uncertain System, 2009, 3(1):3-10. http://www.researchgate.net/publication/228666965_some_research_problems_in_uncertainy_theory
[13]	ZHANG C X, GUO C R.Uncertain block replacement policy with no replacement at failure[J].Journal of Intelligent & Fuzzy Systems, 2014, 27(4):1991-1997. http://dl.acm.org/citation.cfm?id=2684890.2684926
[14]	KE H, YAO K.Block replacement policy with uncertain lifetime[J].Reliability Engineering and System Safety, 2016, 148:119-124. doi: 10.1016/j.ress.2015.12.008
[15]	GAO J W, YAO K, ZHOU J, et al.Reliability analysis of uncertain weighted k-out-of-n systems[J].IEEE Transactions on Fussy Systems, 2018, 26(5):2663-2671. doi: 10.1109/TFUZZ.2018.2806365
[16]	LIU B L, ZHANG Z Q, WEN Y Q.Reliability analysis for complex systems subject to competing failure processes based on chance theoy[J].Applied Mathematical Modelling, 2018, 75:398-413.
[17]	ZHANG Q Y, KANG R, WEN M L.Belief reliability for uncertain random systems[J].IEEE Transactions on Fuzzy Systems, 2018, 26(6):3605-3514. doi: 10.1109/TFUZZ.2018.2838560
[18]	YE Z S, XIE M.Stochastic modelling and analysis of degradation for highly reliable products[J].Applied Stochastic Models in Business and Industry, 2015, 31(1):16-32. doi: 10.1002/asmb.2063
[19]	LIU L, LI X Y, SUN F Q, et al.A general accelerated degradation model based on the Wiener process[J].Materials, 2016, 9(12):981-1000. doi: 10.3390/ma9120981
[20]	LIU B D.Toward uncertain finance theory[J].Journal of Uncertainty Analysis and Applications, 2013, 1(1):1-15. doi: 10.1186/2195-5468-1-1
[21]	LIU B D.Extreme value theorems of uncertain process with application to insurance risk model[J].Soft Computing, 2013(17):549-556. doi: 10.1007/s00500-012-0930-5
[22]	LIU B D.Uncertainty theory:A branch of mathematics for modeling humanuncertainty[M].Berlin:Springer, 2010:133-136.
[23]	HAO S H, YANG J.Dependent competing failure modeling for the GIL subject to partial discharge and air leakage with random degradation initiation time[J].IEEE Transactions on Reliability, 2018, 68(3):1070-1079. http://ieeexplore.ieee.org/document/8514105/
[24]	WANG Q, HE Z Y, LIN S Z, et al.Failure modeling and maintenance decision for GIS equipment subject to degradation and shocks[J].IEEE Transactions on Power Delivery, 2017, 32(2):1079-1088. doi: 10.1109/TPWRD.2017.2655010