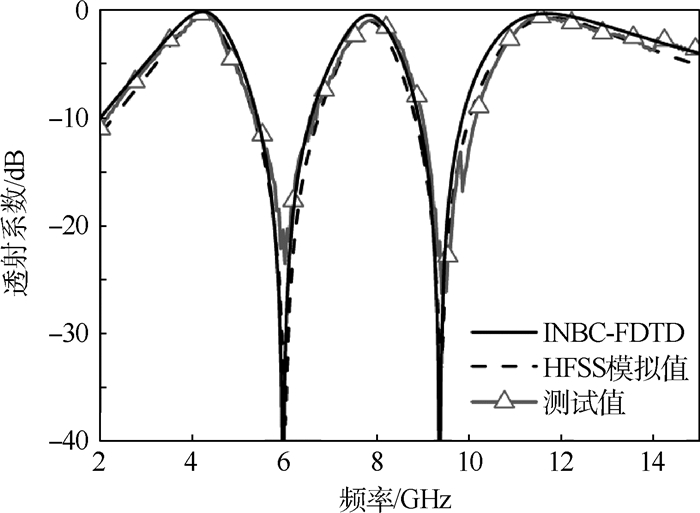
-
摘要:
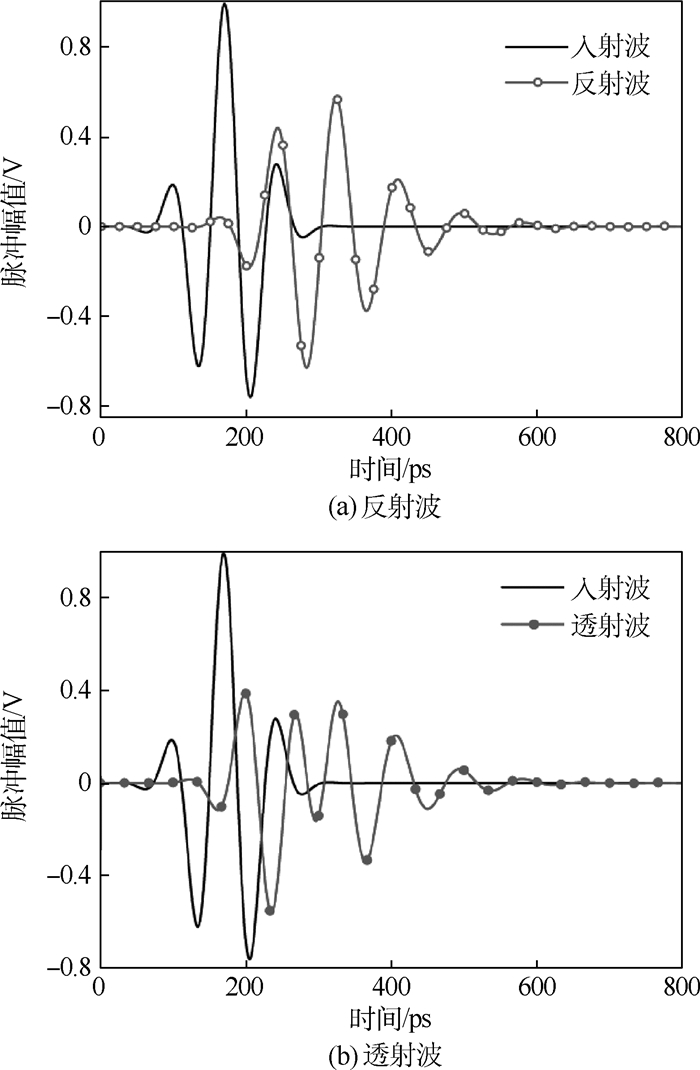
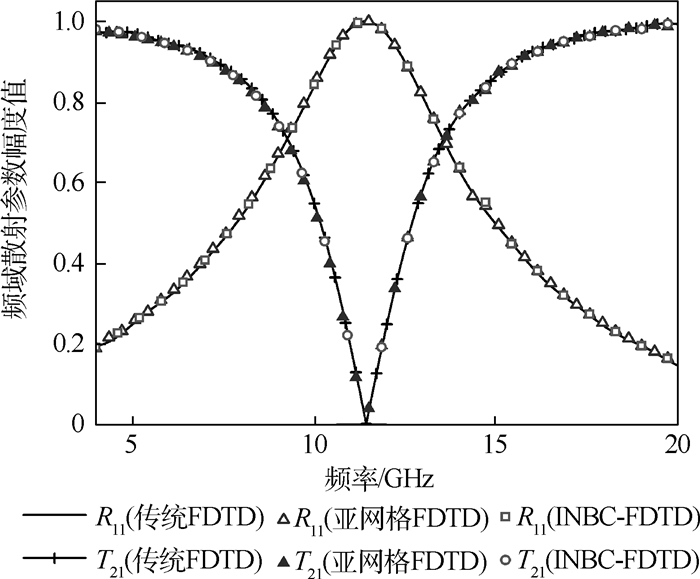
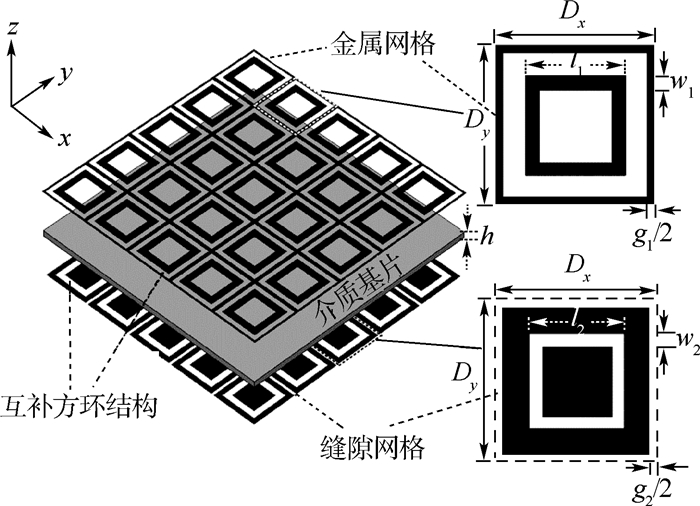
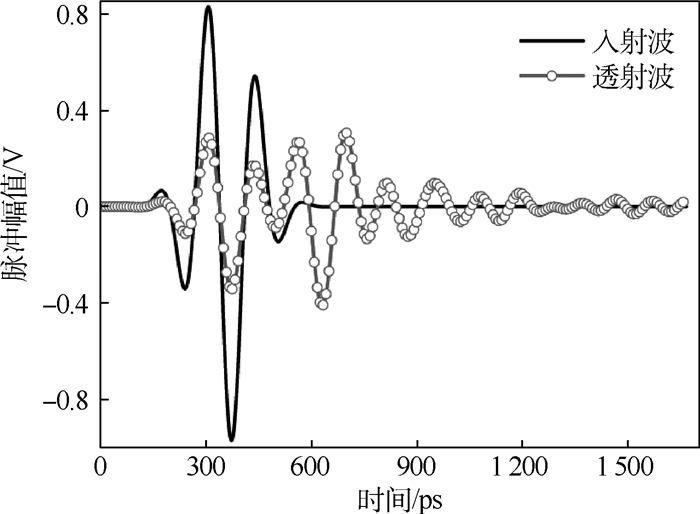
针对周期结构电磁特性参数求解问题，介绍了一种基于网络分析法、矢量拟合法，用来快速求解低剖面周期结构电磁特性参数的内部阻抗边界条件（INBC）与时域有限差分（FDTD）结合的INBC-FDTD计算方法。该方法将金属层的二端口频域阻抗参数曲线先通过矢量拟合法进行有理分式拟合，再对其进行时域变换后嵌入FDTD公式完成对电场、磁场的更新工作。所提方法完整地考虑了在金属层传输的电磁场，其二端口网络阻抗参数全面地考虑了端口之间的互耦问题。
-
关键词:
- 频率选择表面(FSS) /
- 矢量拟合法 /
- 内部阻抗边界条件(INBC) /
- 周期结构 /
- 时域有限差分(FDTD)
Abstract:In order to solve the problem of electromagnetic characteristic parameters of periodic structures, an INBC-FDTD calculation method based on network analysis method and vector fitting method is:introduced in this paper, which can be used to quickly solve the electromagnetic characteristic parameters of low-profile periodic structures.In this method, the two-port frequency domain impedance parameter curve of the metal layer is firstly fitted with rational fractions by the vector fitting method, and then the time domain transform is carried out to embed the FDTD formula to complete the update of the electric field and the magnetic field. The proposed method fully considers electro-magnetic fields transmitted in the metal layer, and its two-port network impedance parameter fully considers the mutual coupling between the ports.
-
图 1 置于两FDTD网格Γ-和Γ+之间的低剖面周期结构侧视图
Figure 1. Side view of low-profile periodic structure placed between two FDTD grids Γ-and Γ+
图 2 二维周期结构的计算空间示意图
Figure 2. Schematic diagram of computational space for two-dimensional periodic structure
图 4 十字贴片型FSS的反射波和透射波时域波形
Figure 4. Reflected wave and transmitted wave of cross patched FSS in time domain
图 5 不同方法得出的频域散射参数幅度值
Figure 5. Amplitude of scattering coefficients in frequency domain obtain by different methods
图 6 方环形结构的互补型FSS及其单元结构示意图
Figure 6. Schematic diagram of complementary FSS with square ring and its unit cell
图 7 方环形结构互补型FSS的透射波时域波形
Figure 7. Transmitted wave of complementary FSS with square ring in time domain
图 8 透射系数的频域波形比较
Figure 8. Comparison of transmission coefficient waves in frequency domain
表 1 提取得到的十字贴片型FSS结构Y矩阵参数频域函数的等效有理式参数：极点pn及留数rn
Table 1. Extracted values of poles (pn) and residues (rn) for Y-matrix coefficients of cross patched FSS
n pn rn(Y11) rn(Y12/Y21) rn(Y22) 1 -7.637 7×106 1.582 5×109 -1.581 5×109 1.581 5×109 2 -3.572 0×1012 -1.812 0×1011 -2.284 1×1010 -4.030 7×1010 3, 4 -5.499 6×107±5.627 9×1010i 4.988 4×107±4.016 6×104i 1.510 7×105±8.706 3×103i -3.096 3×102±1.185 1×103i 5, 6 -5.759 2×108±5.660 8×1010i 1.463 5×107±5.061 7×104i 4.470 2×104±2.012 8×102i 1.468 2×102±1.464 3×103i 7, 8 -7.357 7×107±9.089 0×1010i 2.297 8×108±1.053 0×106i 6.637 8×105±3.934 0×104i 1.191 6×103±9.24×102i 
下载: 导出CSV
表 2 提取得到的十字贴片型FSS结构Y矩阵参数频域函数的等效有理式参数：d
Table 2. Extracted values of d for Y-matrix coefficients of cross patched FSS
Y d Y11 0.050 7 Y12 0.006 4 Y21 0.006 4 Y22 0.011 3
下载: 导出CSV
表 3 不同方法的计算参数
Table 3. Computational parameters for different methods
方法 Δt 单元个数(长×宽×高) 时间步 CPU时间 传统FDTD 16.7 fs 41×41×1 040 60 000 18 d 亚网格FDTD 0.42 ps(粗网格)
16.7 fs(细网格)41×41×80 3 000 14 h INBC-FDTD 0.42 ps 41×41×80 3 000 17 min
下载: 导出CSV
表 4 提取得到的方环形结构互补型FSS结构Y矩阵参数频域函数的等效有理式参数：极点pn及留数rn
Table 4. Extracted values of poles (pn) and residues (rn) for Y-matrix coefficients of complementary FSS with square ring
n pn rn(Y11) rn(Y12/Y21) rn(Y22) 1 -5.589 0×106 2.253 8×109 -1.846 6×109 1.757 6×109 2 -1.665 6×1012 -1.036 4×1011 -2.825 0×1010 -2.410 3×1011 3, 4 -1.991 8×108±3.937 3×1010i 4.629 1×106±1.976 9×105i -1.193 3×107±3.071 4×105i 3.011 3×107±3.314 0×105i 5, 6 -2.030 5×108±3.973 3×1010i 2.964 7×107±1.607 1×105i -7.124 1×107±3.997 4×105i 1.755 8×108±3.953 6×105i 7, 8 -3.195 7×108±6.586 5×1010i 4.565 9×108±3.611 6×106i -2.665 9×108±2.023 7×106i 1.555 8×108±1.25×106i
下载: 导出CSV
表 5 提取得到的方环形结构互补型FSS结构Y矩阵参数频域函数的等效有理式参数：d
Table 5. Extracted values of d for the Y-matrix coefficients of complementary FSS with square ring
Y d Y11 0.062 4 Y12 0.016 9 Y21 0.016 9 Y22 0.144 6
下载: 导出CSV
表 6 两种方法计算参数的比较
Table 6. Comparison of computational parameters for two methods
方法 Δt 单元个数(长×宽×高) 时间步 CPU时间 亚网格
FDTD0.42 ps(粗网格)
16.7 fs(细网格)41×41×80 3 000 14 h INBC-FDTD 0.42 ps 41×41×80 3 000 17 min
下载: 导出CSV
-
[1] OKONIEWSKI M.Three-dimensional subgridding algorithm for FDTD[J].IEEE Transactions on Antennas and Propagation, 1997, 45(3):422-427. doi: 10.1109/8.558657 [2] WHITE M J, ISKONDER M F, HUANG Z.Development of multigrid FDTD code for three dimensional applications[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(10):1512-1517. doi: 10.1109/8.633859 [3] JURGENS T, TAFLOVE A, UMASHANKAR K, et al.Finite-difference time-domain modeling of curved surfaces[J].IEEE Transactions on Antennas and Propagation, 1992, 40(4):357-366. doi: 10.1109/8.138836 [4] DEY S, MITTRA R.A locally conformal finite difference time-domain (FDTD) algorithm for modeling three-dimensional perfectly conducting objects[J].IEEE Microwave and Optical Technology Letters, 1997, 7(9):273-275. [5] JUNKIN G.Conformal FDTD modeling of imperfect conductors at millimeter wave bands[J].IEEE Transactions on Antennas and Propagation, 2011, 59(1):199-205. doi: 10.1109/TAP.2010.2090490 [6] MALONEY J G, SMITH G S.The use of surface impedance concepts in the finite-difference time domain method[J].IEEE Transactions on Antennas and Propagation, 1992, 40(1):38-48. doi: 10.1109/8.123351 [7] BEGGS J H, LUEBBERS R J, YEE K S, et al.Finite difference time-domain implementation of surface impedance boundary conditions[J].IEEE Transactions on Antennas and Propagation, 1992, 40(1):49-56. doi: 10.1109/8.123352 [8] KARKKAINEN M K.FDTD surface impedance model for coated conductors[J].IEEE Transactions on Electromagnetic Compatibility, 2004, 46(2):222-233. doi: 10.1109/TEMC.2004.826891 [9] SHI L, YANG L, MA H, et al.Collocated SIBC FDTD method for coated conductors at oblique incidence[J].Progress in Electromagnetics Research M, 2013, 30:239-252. doi: 10.2528/PIERM13022512 [10] FELIZIANI M.Subcell FDTD modeling of field penetration through lossy shields[J].IEEE Transactions on Electromagetic Compatibility, 2012, 54(2):299-307. doi: 10.1109/TEMC.2011.2160982 [11] NAYYERI V, SOLEIMANI M, RAMAHI O.Modeling graphene in the finite-difference time domain method using a surface boundary condition[J].IEEE Transactions on Antennas and Propagation, 2013, 61(8):4176-4182. doi: 10.1109/TAP.2013.2260517 [12] BOUZIANAS G D, KANTARTZIS N V, YIOULTSIS T V, et al.Consistent study of graphene structures through the direct incorporation of surface conductivity[J].IEEE Transactions on Magnetics, 2014, 50(2):161-164. doi: 10.1109/TMAG.2013.2282332 [13] GUSTAVSEN B, SEMLYEN A.Rational approximation of frequency domain responses by vector fitting[J].IEEE Transactions on Power Delivery, 1999, 14(3):1052-1061. doi: 10.1109/61.772353 [14] KUNZ K S, LUEBBERS R J.The finite difference time domain method for electromagnetics[M].Boca Raton:CRC Press, 1993. [15] WANG D, CHE W, CHANG Y, et al.A low-profile frequency selective surface with controllable tri-band characteristics[J].IEEE Microwave and Wireless Components Letters, 2013, 12:468-471. -
下载:
点击查看大图
计量
- 文章访问数: 431
- HTML全文浏览量: 62
- PDF下载量: 189
- 被引次数: 0
