基于GNSS测量的天宫二号质心确定

金哲阳; 王文彬; 刘江凯

doi:10.13700/j.bh.1001-5965.2020.0019

基于GNSS测量的天宫二号质心确定

doi: 10.13700/j.bh.1001-5965.2020.0019

金哲阳^{1, 2},
王文彬^{1, 2, ,},
刘江凯^{1, 2}

1.
中国科学院空间应用工程与技术中心, 北京 100094
2.
中国科学院大学, 北京 100049

基金项目:

中国科学院重点部署项目 ZDRW-KT-2019-1

中国科学院联合基金 6141A01011703

详细信息

作者简介:
金哲阳男, 硕士研究生。主要研究方向: 航天器轨道确定

王文彬男, 博士, 高级工程师, 硕士生导师。主要研究方向: 航天器精密定轨与自主导航

刘江凯男, 博士研究生。主要研究方向: 航天器自主导航

通讯作者:
王文彬, E-mail: wangwenbin@csu.ac.cn

中图分类号: V412.41
计量
- 文章访问数: 772
- HTML全文浏览量: 204
- PDF下载量: 147
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-15
- 录用日期: 2020-10-16
- 网络出版日期: 2021-04-20

Center of mass estimation of Tiangong-2 spacecraft using GNSS measurement

JIN Zheyang^{1, 2},
WANG Wenbin^{1, 2
, ,},
LIU Jiangkai^{1, 2}

1.
Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds:

Key Research Program of the Chinese Academy of Sciences ZDRW-KT-2019-1

CAS Joint Fund 6141A01011703

More Information

Corresponding author: WANG Wenbin, E-mail: wangwenbin@csu.ac.cn

摘要

摘要:
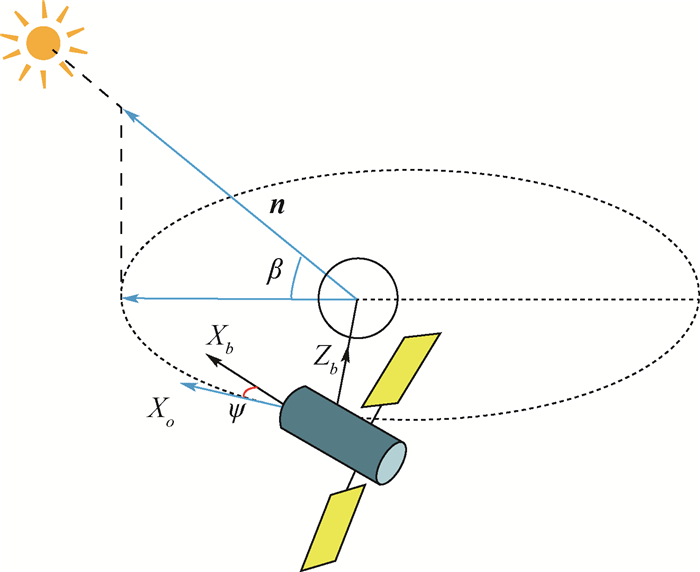
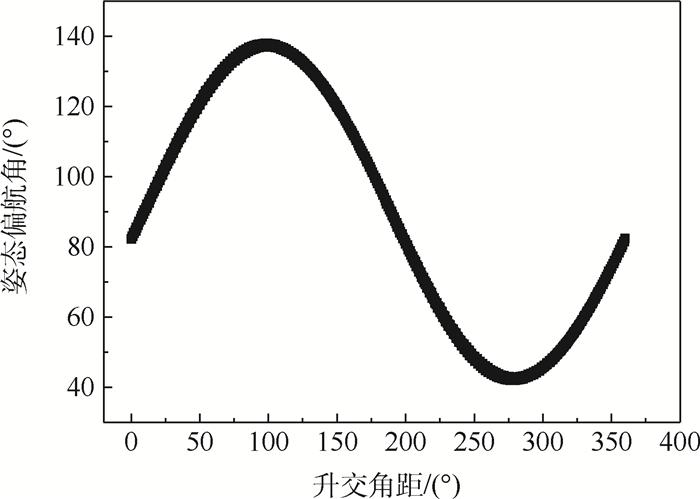
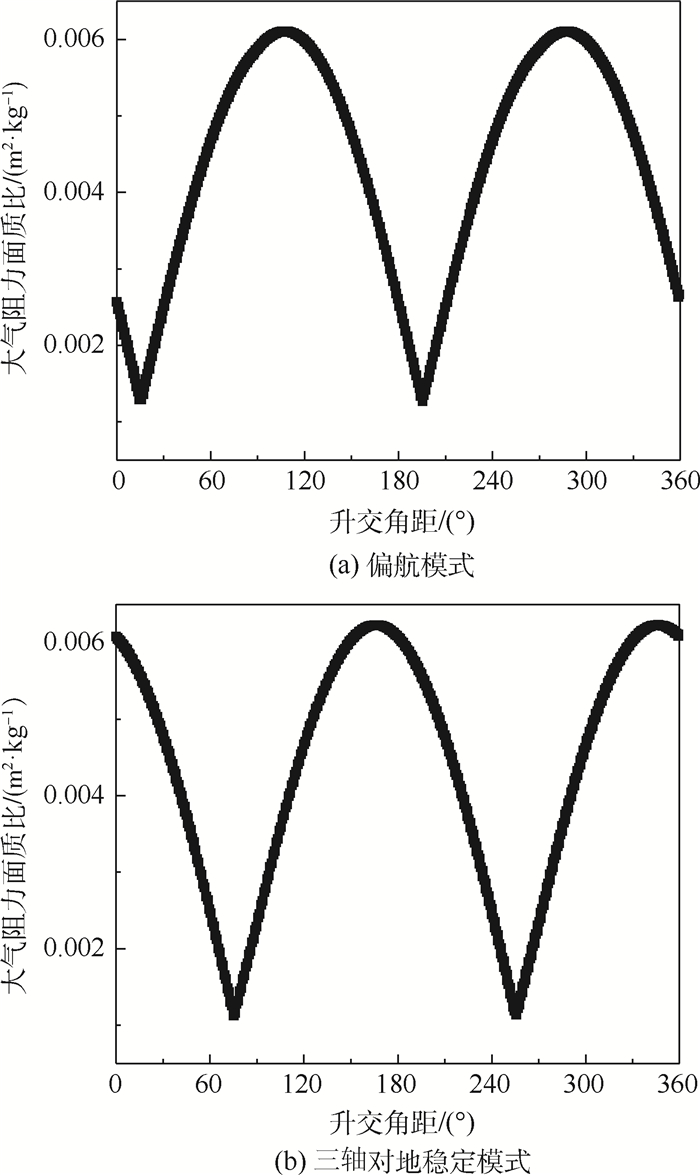
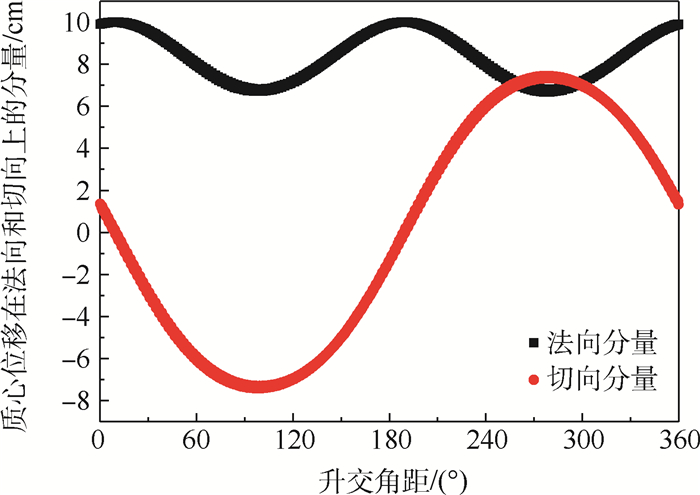
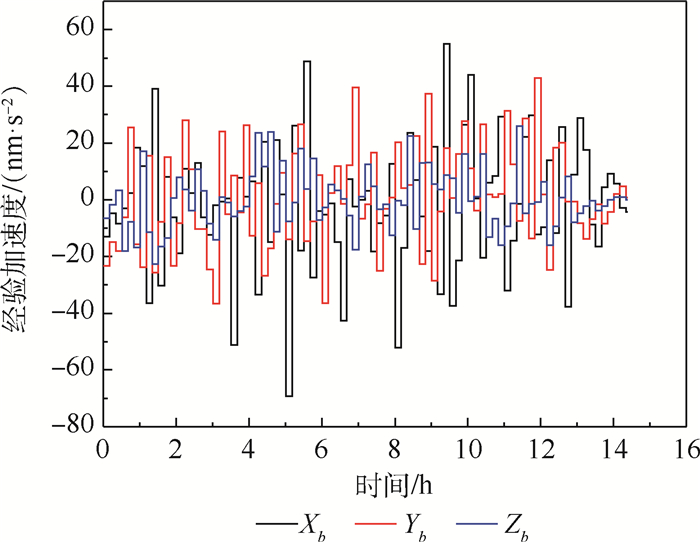
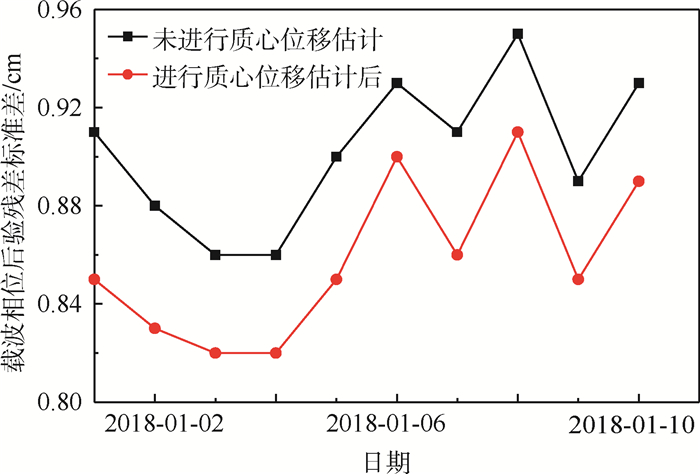
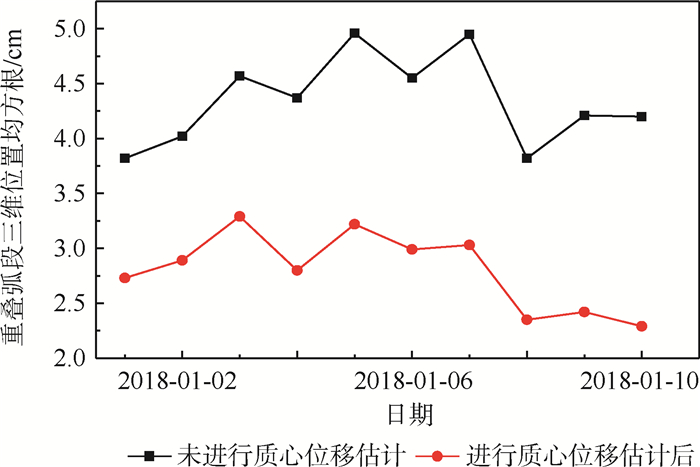
由于轨道机动燃料消耗，科学载荷加载、分离，以及伴飞小卫星在轨释放等原因引起天宫二号空间站质心(COM)发生位移，从而影响天宫二号的动力学质心定轨精度。针对这一问题，提出了基于全球导航卫星系统(GNSS)测量数据的简化动力学质心估计方法。燃料消耗是引起天宫二号质心发生位移的主要原因，质心在本体坐标系X轴方向位移最为显著。利用GNSS测量数据对天宫二号进行质心估计和精密定轨，在三轴对地稳定姿态下，本体坐标系X轴方向与轨道切向重合，定轨结果对本体坐标系X轴方向的质心位移并不敏感。但在连续偏航模式下，本体坐标系X轴在轨道法向上有较大分量，X轴方向的质心位移对基于GNSS测量计算的精密定轨结果有较大影响。定性和定量分析结果表明：偏航姿态模式下天宫二号本体坐标系X轴方向质心位移估计具有可行性。天宫二号实测数据计算结果表明：与未做质心估计的定轨结果进行对比，质心估计后表征轨道动力学建模误差的经验加速度补偿水平在轨道径向、切向和法向上分别降低62%、50%和65%；载波相位后验残差标准差降低0.04 cm；精密轨道与全球激光测距数据比较精度提高0.86 cm。所提方法可以应用于大型低轨航天器在轨质心估计。
- 天宫二号 /
- 质心(COM)估计 /
- 偏航姿态模式 /
- 经验加速度 /
- 激光测距
Abstract:
Due to fuel consumption of orbital maneuvers, payloads' load and separation, and the release of small satellite, the Center of Mass(COM) of Tiangong-2 space laboratory moves. To solve this problem, a reduced orbit dynamic determination and COM estimation method is given based on Global Navigation Satellite System (GNSS) measurement data in this paper. Fuel consumption is the main reason for the COM of Tiangong-2 moves. The COM mainly moves along the X-axis of Tiangong-2 body-fixed coordinate system. The COM estimation and precise orbit determination of Tiangong-2 are performed using GNSS measurement data. And in a three-axis earth-pointing stabilization attitude mode, the orbit determination results are not sensitive to the displacement of COM in the X-axis of Tiangong-2 body-fixed coordinate system since the X-axis of Tiangong-2 body-fixed coordinate system coincides with the tangential direction of the orbit. However, in a yaw-steering mode, the X-axis of Tiangong-2 body-fixed coordinate system has a large projection on the orbital normal direction, which makes the displacement of COM in the X-axis of Tiangong-2 body-fixed coordinate system have a greater impact on the precision orbit determination results based on GNSS measurement calculation. And the qualitative and the quantitative analysis results show that the COM estimation is feasible in a yaw-steering attitude mode. Compared with the results without considering COM estimation, the Tiangong-2 measurement data calculation results considering COM estimation show that the empirical accelerations which represent orbital dynamics modeling error in the radial, tangential and normal directions are reduced by 62%, 50% and 65%, respectively, and the standard deviation of post-residuals of the carrier phase is reduced by 0.04 cm. Besides, the comparison accuracy of precision orbit data and the global laser ranging improves by 0.86 cm. The method proposed in this paper can be applied to COM estimation of the large-scale low-earth-orbit spacecraft.
- Tiangong-2 /
- Center of Mass (COM) estimation /
- yaw-steering attitude mode /
- empirical acceleration /
- laser ranging

HTML全文

图 1 天宫二号结构和象限线示意图

Figure 1. Illustration of Tiangong-2 structure and quadrant line definition

下载: 全尺寸图片幻灯片

图 2 轨道坐标系示意图

Figure 2. Illustration of orbital coordinate system

下载: 全尺寸图片幻灯片

图 3 天线安装位置及天线法线示意图

Figure 3. Illustration of position and normal direction of antenna

下载: 全尺寸图片幻灯片

图 4 天宫二号偏航姿态运动示意图

Figure 4. Illustration of Tiangong-2 yaw-steeringattitude mode

下载: 全尺寸图片幻灯片

图 5 姿态偏航角变化示意图

Figure 5. Illustration of yaw angle change

下载: 全尺寸图片幻灯片

图 6 Cylinder-wing模型示意图

Figure 6. Illustration of model of Cylinder-wing

下载: 全尺寸图片幻灯片

图 7 偏航模式和三轴对地稳定模式下，大气阻力面质比在不同升交角距下的变化规律

Figure 7. Law of the change of atmospheric drag mass of atmospheric drag in attitude mode of yaw steering and in attitude mode of three-axis Earth-pointing stabilization under different argument of latitude

下载: 全尺寸图片幻灯片

Figure 8. Positional relationship among satellite reference COM, dynamic COM and antenna phase center

下载: 全尺寸图片幻灯片

图 9 偏航模式下，本体坐标系X_b轴10 cm质心位移在轨道切向和法向上的分量变化

Figure 9. Component changes of X_b-axis 10 cm-offsets of COM in along-track and cross-track directions in attitude mode of yaw steering

下载: 全尺寸图片幻灯片

图 10 偏航模式下，质心位移估计后本体坐标系下3个方向的经验加速度

Figure 10. Empirical acceleration after COM offset estimation in three directions in satellite-body-fixed coordinate system in attitude mode of yaw steering

下载: 全尺寸图片幻灯片

图 11 2018年1月1日—2018年1月10日的轨道后验残差标准差变化

Figure 11. Changes of standard deviation of post-fit residuals from January 1st, 2018 to January 10th, 2018

下载: 全尺寸图片幻灯片

图 12 经验加速度的补偿水平在轨道径向、切向和法向上的变化

Figure 12. Changes of radial, along-track and cross-track directions in compensation level of empirical acceleration

下载: 全尺寸图片幻灯片

图 13 重叠弧段精度变化

Figure 13. Change of accuracy of overlapping arc

下载: 全尺寸图片幻灯片

姿态角示意图

Illustration of attitude angle

下载: 全尺寸图片幻灯片

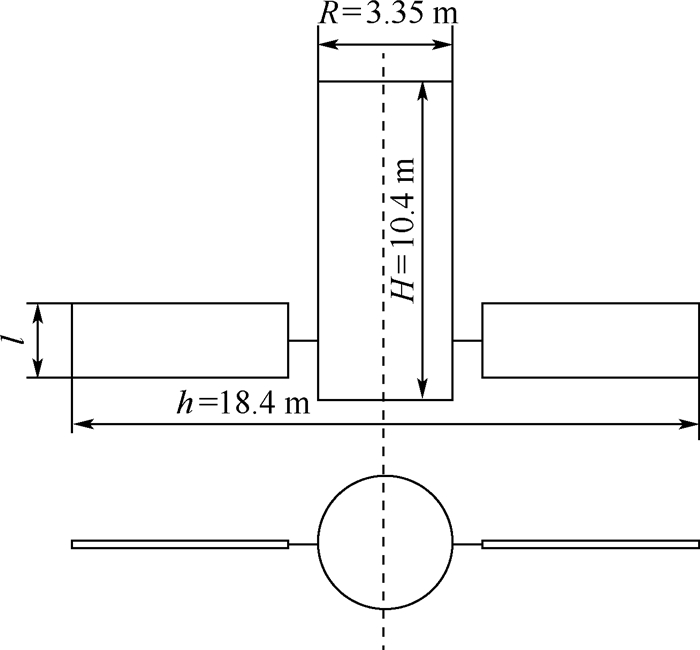
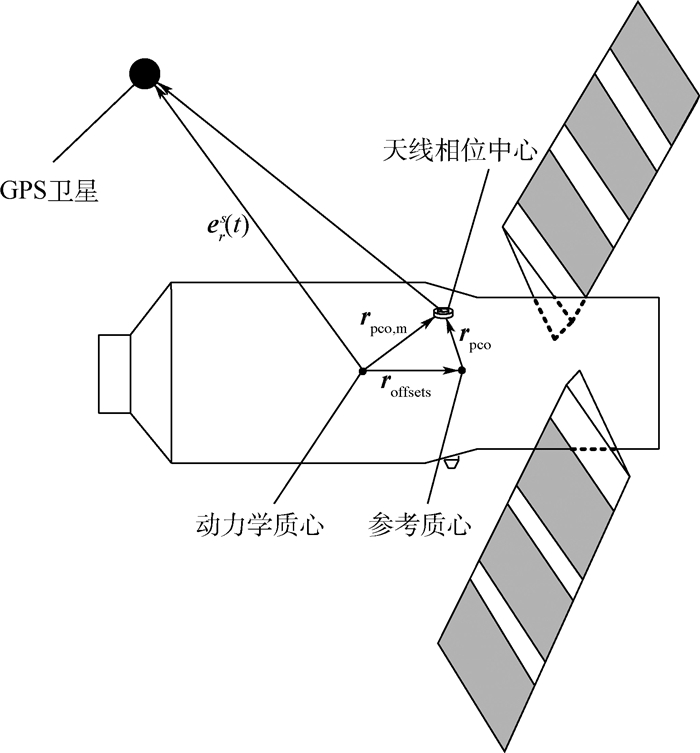
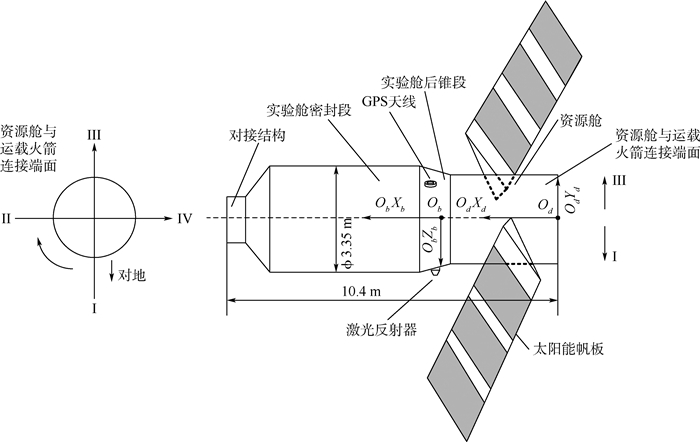
表 1 测量载荷与发射前参考质心的位置

Table 1. Positions of measured loads and reference COM before launch

位置	X_d/cm	Y_d/cm	Z_d/cm
天线相位中心	428.66	158.5	-101.31
激光角反射镜	414.88	-159.57	-0.09
发射前参考质心	416.03	0.63	0.53

下载: 导出CSV

表 2 本体坐标系X_b方向10 cm的质心位移变化对定轨结果的影响分析

Table 2. Analysis of influence of 10 cm COM offset in X_b-axis direction on orbit determination results

日期	R_x/cm	R_y/cm	R_z/cm
2018-01-08	6.39	6.81	2.58
2018-01-09	5.69	7.28	1.67
2018-01-10	5.42	7.63	1.85
平均值	5.83	7.24	2.03

下载: 导出CSV

表 3 本体坐标系Y_b方向10 cm的质心位移变化对定轨结果的影响分析

Table 3. Analysis of influence of 10 cm COM offset in Y_b-axis direction on orbit determination results

日期	R_x/cm	R_y/cm	R_z/cm
2018-01-08	7.8	6.3	1.00
2018-01-09	7.49	6.52	0.85
2018-01-10	7.83	6.58	1.04
平均值	7.71	6.47	0.96

下载: 导出CSV

表 4 本体坐标系Z_b方向10 cm的质心偏移变化对定轨结果的影响分析

Table 4. Analysis of influence of 10 cm COM offset in Z_b-axis direction on orbit determination results

日期	R_x/cm	R_y/cm	R_z/cm
2018-01-08	3.18	0.61	8.14
2018-01-09	2.75	0.53	8.86
2018-01-10	3.08	0.44	8.65
平均值	3.00	0.53	8.55

下载: 导出CSV

表 5 根据燃料消耗推算的天宫二号质心位置和天线相位中心位置

Table 5. Position of COM and antenna phase center of Tiangong-2 computed by fuel consumption

阶段	发生时间(UTC)	质量/kg		质心位置(整体坐标系)/cm	天线相位中心位置(本体坐标系)/cm
阶段	发生时间(UTC)	天宫二号整器	剩余燃料	质心位置(整体坐标系)/cm	天线相位中心位置(本体坐标系)/cm
轨控	2016-09-16 08:58:55	8 406.4	692.4	(416.03, 0.63, 0.53)	(12.63, -101.84, -157.87)
阶段A~阶段C	2018-01-01 00:00:00	8 488.97	889.88	(393.29, 1.55, 0.53)	(35.37, -101.84, -156.95)

下载: 导出CSV

表 6 所选实验时段的具体说明

Table 6. Specific instructions for selected experimental period

时段名称	时段	时段内天宫二号姿态模式	时段内是否有激光观测数据	具体实验方法
阶段A	2018-01-01—2018-01-10	连续偏航	无	对本体坐标系X_b、Y_b、Z_b 3个方向同时进行质心位移估计，给出质心位移，并对比质心估计前后的定轨结果
阶段B	2018-08-20—2018-08-24	三轴对地稳定	有	利用阶段A估计的质心位移进行质心校正后，完成精密定轨，并对轨道进行激光外符合校验
阶段C	2018-08-27—2018-08-30	连续偏航	有	利用阶段A估计的质心位移进行质心校正后，完成精密定轨，并对轨道进行激光外符合校验

下载: 导出CSV

表 7 偏航姿态模式下，本体坐标系3个方向的质心位移估计值及不确定度

Table 7. Estimates and uncertainties of COM offset in three directions in satellite-body-fixed coordinate system in attitude mode of yaw steering

日期	X_b/cm	Y_b/cm	Z_b/cm
2018-01-01	-16.54±0.35	-7.49±0.74	1.20±0.13
2018-01-02	-16.09±0.36	-5.68±0.86	1.21±0.13
2018-01-03	-16.26±0.41	-4.69±1.07	1.04±0.11
2018-01-04	-16.02±0.43	-6.76±1.38	1.11±0.14
2018-01-05	-15.74±0.41	-6.53±1.34	1.29±0.16
2018-01-06	-16.13±0.44	-9.57±2.19	1.02±0.13
2018-01-07	-15.30±0.48	-7.19±3.03	0.94±0.14
2018-01-08	-15.54±0.47	-3.84±3.36	0.80±0.14
2018-01-09	-15.79±0.53	-11.25±5.09	0.87±0.16
2018-01-10	-15.03±0.43	-10.87±3.27	0.88±0.19
平均值	-15.84	-7.39	1.04
标准差	0.46	2.49	0.16

下载: 导出CSV

表 8 三轴对地稳定姿态下，卫星激光测距比对结果

Table 8. SLR comparison results in attitude mode of three-axis Earth-pointing stabilization

日期	未应用质心位移量的定轨结果与激光测距比较残差/cm	应用质心位移量的定轨结果与激光测距比较残差/cm
2018-08-20	3.14	3.01
2018-08-21	3.29	3.17
2018-08-22	2.96	2.76
2018-08-23	3.03	2.95
2018-08-24	3.27	3.08
平均值	3.14	2.99

下载: 导出CSV

表 9 连续偏航姿态下，卫星激光测距比对结果

Table 9. SLR comparison results in attitude mode of yaw steering

日期	未应用质心位移量的定轨结果与激光测距比较残差/cm	应用质心位移量的定轨结果与激光测距比较残差/cm
2018-08-27	3.45	2.73
2018-08-28	3.12	2.12
2018-08-29	2.93	2.15
2018-08-30	2.82	1.87
平均值	3.08	2.22

下载: 导出CSV

参考文献(21)

[1]	MONTENBRUCK O, VAN H T, KROES R, et al. Reduced dynamic orbit determination using GPS code and carrier measurements[J]. Aerospace Science and Technology, 2005, 9(3): 261-271. doi: 10.1016/j.ast.2005.01.003
[2]	秦建, 郭金运, 孔巧丽, 等. Jason-2卫星星载GPS数据cm级精密定轨[J]. 武汉大学学报(信息科学版), 2014, 39(2): 137-141. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201402003.htm QIN J, GUO J Y, KONG Q L, et al. Precise orbit determination of Jason-2 with precision of centimeters based on satellite-borne GPS technique[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 137-141(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH201402003.htm
[3]	LI K, ZHOU X, WANG W, et al. Centimeter-level orbit determination for TG02 spacelab using onboard GNSS data[J]. Sensors, 2018, 18(8): 2671. doi: 10.3390/s18082671
[4]	张强. 采用GPS与北斗的低轨卫星及其编队精密定轨关键技术研究[D]. 武汉: 武汉大学, 2018: 22-35. ZHANG Q. Research on the key technologies of precise orbit determination for low earth orbit satellites and their formation using GPS and BDS[D]. Wuhan: Wuhan University, 2018: 22-35(in Chinese).
[5]	秦显平. 星载GPS低轨卫星定轨理论及方法研究[J]. 测绘科学与工程, 2010, 30(1): 77-78. https://cdmd.cnki.com.cn/Article/CDMD-90008-1011057310.htm QIN X P. Research on precision orbit determination theory and method of low earth orbiter based on GPS technique[J]. Science of Surveying and Mapping, 2010, 30(1): 77-78(in Chinese). https://cdmd.cnki.com.cn/Article/CDMD-90008-1011057310.htm
[6]	BRUINSMA S, TAMAGNAN D, BIANCALE R. Atmospheric densities derived from CHAMP/STAR accelerometer observations[J]. Planetary and Space Science, 2004, 52(4): 297-312. doi: 10.1016/j.pss.2003.11.004
[7]	戴小蕾. 基于平方根信息滤波的GNSS导航卫星实时精密定轨理论与方法[D]. 武汉: 武汉大学, 2016: 18-20. DAI X L. Real-time precise GNSS satellite orbit determination using the SRIF method: Theory and implementation[D]. Wuhan: Wuhan University, 2016: 18-20(in Chinese).
[8]	刘伟, 俞洁, 杨立峰, 等. GEO卫星在轨横向质心快速估算方法[J]. 航天器工程, 2016, 25(5): 39-44. doi: 10.3969/j.issn.1673-8748.2016.05.006 LIU W, YU J, YANG L F, et al. Method of in-orbit lateral centroid fast estimation of GEO satellite[J]. Spacecraft Engineering, 2016, 25(5): 39-44(in Chinese). doi: 10.3969/j.issn.1673-8748.2016.05.006
[9]	TANYGIN S, WILLIAMS T. Mass property estimation using coasting maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(4): 625-632. doi: 10.2514/2.4099
[10]	郭正勇, 张增安, 汪礼成, 等. 一种基于推力器控制的卫星质心在轨估算方法研究[J]. 上海航天, 2017, 34(5): 76-82. https://www.cnki.com.cn/Article/CJFDTOTAL-SHHT201705012.htm GUO Z Y, ZHANG Z A, WANG L C, et al. Study of on-orbit estimation method of satellite'centroid based on thrust control[J]. Aerospace Shanghai, 2017, 34(5): 76-82(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SHHT201705012.htm
[11]	谭沧海, 梁翠娜, 薛宏伟. 伪距定位算法中天线相位中心偏差的修正及误差分析[J]. 现代导航, 2017, 8(5): 328-333. https://www.cnki.com.cn/Article/CJFDTOTAL-XDDH201705004.htm TAN C H, LIANG C N, XUE H W. Analysis and correction of antenna phase center offsets on pseudo-range positioning algorithm[J]. Modern Navigation, 2017, 8(5): 328-333(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XDDH201705004.htm
[12]	辛宁, 邱乐德, 张立华, 等. 一种重力卫星质心在轨标定算法[J]. 中国空间科学技术, 2013, 33(4): 9-15. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKJ201304004.htm XIN N, QIU L D, ZHANG L H, et al. Study on on-orbit calibration of center of mass for gravity satellite[J]. Chinese Space Science and Technology, 2013, 33(4): 9-15(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKJ201304004.htm
[13]	李洪银, 屈少波, 白彦峥, 等. 静电悬浮加速度计在轨质心位置的最小二乘估计[J]. 地球物理学报, 2017, 60(3): 897-902. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201703005.htm LI H Y, QU S B, BAI Y Z, et al. Least squares estimation of in-orbit mass center position of the electrostatic accelerometer[J]. Chinese Journal of Geophysics, 2017, 60(3): 897-902(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX201703005.htm
[14]	陈光锋, 唐富荣, 薛大同. 重力卫星在轨质心修正原理[J]. 宇航学报, 2005, 26(5): 567-570. https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB200505007.htm CHEN G F, TANG F R, XUE D T. The trim principle of center of mass of gravity satellite during orbit flight[J]. Journal of Astronautics, 2005, 26(5): 567-570(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB200505007.htm
[15]	WANG W, LIU J, SHUA L, et al. Precise orbit determination of large-scale spacecraft in low earth orbit: Preliminary results[C]//Proceedings of the 68th International Astronautical Congress (IAC), 2017: 3-12.
[16]	SHAO K, GU D, JU B, et al. Analysis of Tiangong-2 orbit determination and prediction using onboard dual-frequency GNSS data[J]. GPS Solutions, 2020, 24(1): 11. doi: 10.1007/s10291-019-0927-y
[17]	KROES R. Precise relative positioning of formation flying spacecraft using GPS[D]. The Netherland: Delft University of Technology, 2006: 56-63.
[18]	WANG W, GAO Y. Effective empirical acceleration modeling and its application to enhanced-accuracy orbit prediction[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, Aerospace Technology Japan, 2016, 14(30): 39-45. doi: 10.2322/tastj.14.pd_39
[19]	JIA T U, GU D F, YI W U, et al. Phase residual estimations for PCVs of spaceborne GPS receiver antenna and their impacts on precise orbit determination of GRACE satellites[J]. Chinese Journal of Aeronautics, 2012, 25(4): 631-639. http://www.cnki.com.cn/Article/CJFDTotal-HKXS201204017.htm
[20]	RIM H J, YOON S, SCHUTZ B, et al. Effect of center of mass position error on icesat precision orbit determination[C]//AIAA/AAS Astrodynamics Specialist Conference. Reston: AIAA, 2010: 77-79.
[21]	CHOI K R. Jason-1 precision orbit determination using GPS combined with SLR and DORIS tracking data[D]. Austin: The University of Texas at Austin, 2003: 43-47.