-
摘要:
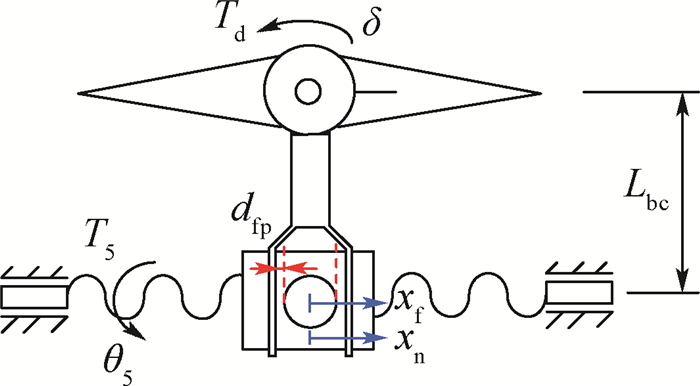
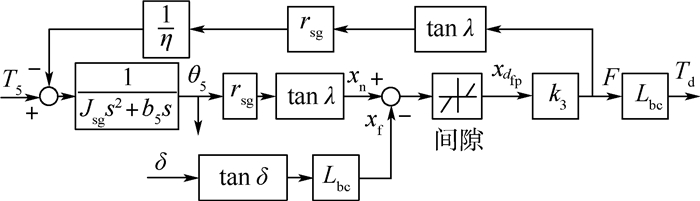
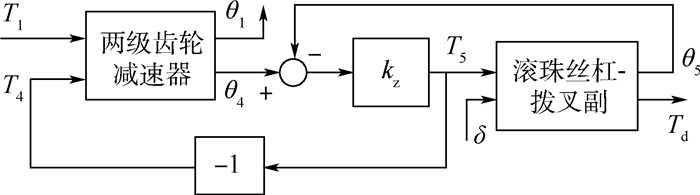
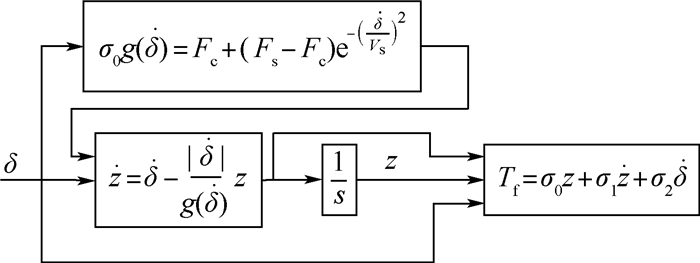
颤振是一种危险的气动弹性失稳形式，舵机动刚度对舵系统的颤振特性具有不可忽视的影响，因此舵机的精确建模与仿真分析十分有必要。针对此问题，提出了一种电动舵机模块化建模方法及动刚度计算机模拟方法。以“直流电机-减速齿轮-滚珠丝杠-拨叉副”典型结构的电动伺服舵机为对象，将其分解为具备核心功能的子模块，充分考虑了实际结构中可能出现的主要非线性因素，再根据子模块之间的连接关系来搭建整体的舵机模型。基于该舵机模型，提出了利用步进正弦扫频信号激励、最小二乘法数据处理得到动刚度的计算方法，并以某舵机为算例，开展了舵机主要线性参数及非线性因素对舵机动刚度影响的研究。电动舵机模块化建模方法通用性好，便于不同舵机的拓展。电机转子阻尼、减速器的传动比以及输出轴处的阻尼对舵机的动刚度影响很大，间隙、接触刚度和摩擦这3类非线性因素对舵机的动刚度特性也具有重要的影响。
Abstract:Flutter is a dangerous aeroelastic instability form. The influence of actuator dynamic stiffness on the fin-actuator system flutter characteristics cannot be ignored. Therefore, accurate actuator modeling and simulation are necessary. A modular modeling method and dynamic stiffness computer simulation method for electromechanical actuator are proposed. The object is the actuator composed of DC motor, reduction gear and ball screw-fork. It is divided into submodules with core functions. The main nonlinear factors that may appear are fully considered. Then the whole actuator model is built according to the connection between the submodules. Based on the above, a calculation method using step sine sweep signal as excitation and processing the data by least square method is proposed. Taking a certain actuator as an example, the influence of the actuator main linear and nonlinear parameters on the dynamic stiffness is studied. The modular modeling method has good generality, which is convenient for the modeling of different actuators. The damping of the motor rotor, the transmission ratio of the reducer and the damping at the output shaft have a great influence on the dynamic stiffness, and three nonlinear factors, clearance, contact stiffness and friction, also have important influence.
-
Key words:
- electromechanical actuator /
- modeling /
- dynamic stiffness /
- aeroservoelasticity /
- nonlinearity
-
捷联惯导是一种自主式导航系统，因其抗干扰性性强、隐蔽性好等特点，被广泛应用于军事和民用领域，包括潜艇、导弹、航空以及地面的导航与定位系统等[1]。众所周知，初始对准是惯导系统开始导航之前必不可少的准备工作，由于初始对准的精度和对准所需的时间直接影响到后续导航的精度和惯导系统的启动时间，所以，初始对准技术成为近年来的研究热点。目前常用的对准方法包括传统的解析式粗对准结合卡尔曼滤波实现的静基座对准方法[2]、通过提高系统的可观测性进而提高对准精度的多位置对准方法[3-4]、传递对准方法[5-7]、摇摆晃动条件下或是行进中实现的动基座条件下的对准方法[8-17]。其中，在摇摆晃动基座条件下的一类对准方法是将初始捷联矩阵分解为惯性坐标系相对导航坐标系的转换矩阵、初始载体坐标系相对惯性坐标系的矩阵和载体坐标系相对初始载体坐标系的转换矩阵的乘积的形式，通过跟踪重力加速度的明显运动获得其在惯性坐标系和初始载体坐标系的投影来求解初始载体坐标系与惯性坐标系之间的转换矩阵，进而实现初始对准的惯性坐标系对准方法[15, 18-19]。
为了提高载车的机动性，实现行进间对准，本文提出一种快速行进间粗对准方法，受惯性坐标系对准方法的启发，将捷联矩阵分解为3个矩阵乘积的形式，但初始载体坐标系相对惯性坐标系的转换矩阵是通过GPS获得的载体速度在惯性坐标系的投影和里程计获得的速度在初始载体坐标系的投影来求解。与现有的对准方法相比，本文提出的对准方法没有用到加速度计的测量信息，这使得该方法是一种完全在行进中实现对准的方法，同时，也使得该方法不能在静止或摇摆晃动基座条件下完成对准；与现有的行进间对准方法[17, 20-21]相比，该方法可在较短时间内获得较高的对准精度。该方法的特点是对准精度依赖于载体的运行速度，对准时间短。
1. 坐标系定义
1) 地球坐标系(e系)：Oxe轴在赤道平面内且指向中央子午线，Oze轴沿地球自转轴方向，3轴构成右手坐标系；e系与地球固连，相对惯性空间的旋转角速度为地球的自转角速度ωie。
2) 初始时刻地球坐标系(e0系)：在初始对准开始时刻(即t=t0=0 时)Oxe0轴在赤道平面内且指向当地经线，Oze0轴沿地球自转轴方向，3轴构成右手坐标系；e0系也与地球固连，相对惯性空间的旋转角速度为地球的自转角速度ωie。
3) 初始时刻惯性坐标系(i0系)：在对准开始时刻i0系的坐标轴与e0系对应的坐标轴重合，且i0 系相对惯性空间静止，即e0系相对i0系沿Ozi0轴以角速度ωi0e旋转。
4) 导航坐标系(n系)：选取“东-北-天”坐标系为导航坐标系。
5) 初始时刻导航坐标系(n0系)：把开始对准时刻的导航坐标系定义为n0系，它相对于地球表面不动。
6) 载体坐标系(b系)：定义“右-前-上”坐标系为载体坐标系。
7) 初始时刻载体惯性坐标系(ib0系)：在对准开始时刻ib0系与b系重合，且ib0系相对惯性空间静止。
2. 对准算法
在行进间对准过程中，捷联矩阵Cbn(t)随时间变化，为了求得当前时刻的Cbn(t),将Cbn(t)的求解分解成3个矩阵乘积的形式[22]，即
(1) 式中：Ci0n(t)为i0系到n系的转换矩阵；Cib0i0为ib0系到i0系的转换矩阵；Cbib0(t)系为b系到ib0系的转换矩阵，下面分别对这3个矩阵进行求解;t为对准时间。
2.1 求解矩阵Ci0n(t)
转换矩阵Ci0n(t)可以写为
(2) 式中：Cen(t)为e系到n系的转换矩阵；Cn0e为n0系到e系的转换矩阵；Ce0n0为e0系到n0系的转换矩阵；Ci0e0(t)为i0系到e0系的转换矩阵，并且Cen(t)、Cn0e和Ce0n0可由载体所在位置的经度和纬度求得，Ci0e0(t)可由e0系相对i0系转过的角度确定，具体关系[23]为
(3) 式中：λ0和L0为对准开始时刻捷联惯导所在位置的经度和纬度；λt和Lt为t时刻的实时经度和纬度。将式(3)代入式(2)经过整理可以得到
(4) 由于GPS能够提供实时的经度和纬度信息，根据式(4)可以得到矩阵Ci0n(t)的实时值，在求得Ci0n(t)之后，由式(1)可知，要想得到Cbn(t)，还需要求解Cib0i0和Cbib0(t)，接下首先来求解Cbib0(t)。
2.2 求解矩阵Cbib0(t)
变换矩阵Cbib0(t)可通过陀螺仪采样输出，利用捷联惯导姿态更新算法求得，设b系相对ib0系的转动四元数为
(5) 式中：q0~q3为Q的元素；ib、jb和kb为相应的矢量。Q的即时修正可通过解下面的四元数微分方程来实现：
(6) 式中：ωib0bb=[ωib0bxbωib0bybωib0bzb]T为b系相对ib0系的旋转角速度在b系的投影，可以由陀螺仪的输出直接获得，由于在对准的开始时刻b系与ib0系重合，所以此时b系相对ib0系的转动四元数为Q0=[1 0 0 0]T，从而根据式(6)可以得到实时的Q，在获得Q后，矩阵Cb0bi(t)便可以由式(7)求得。
(7) 2.3 求解常值矩阵Cib0i0
常值矩阵Cib0i0表示ib0系到i0系的转换矩阵，只要同时获得某一物理量在ib0系和i0系中的投影，便可求得Cib0i0，基于这一想法，寻求满足要求的物理量便成了求解Cib0i0的关键点，这也是本文的创新之处。
在GPS和里程计辅助的惯导系统中，GPS可以提供载体相对地球在n系的实时速度Vn(t)=[VEn VNnVUn]T，VnE、VnN和VnU分别为载体沿东向、北向和天向的速度。里程计可以提供载体相对地球在b系的实时速度Vb(t)=[0 Vyb 0]T，其中Vyb为载体前进方向的速度。不难发现，可以由Vn(t)获得载体在i0系的速度投影V0i(t)如式(8)所示，同理，可以由Vb(t)获得载体在ib0系的速度投影Vb0i(t)如式(9)所示。
(8) 
(9) 式中：Cni0(t)=(Ci0n(t))T可以由式(4)获得，Cbib0(t)可以由式(7)得到。
在获得Vi0(t)和Vib0(t)之后，便可用类似解析式粗对准的方法来求解Cib0i0，很明显存在式(10)的关系，Cib0i0=(Cib0i0)T。
(10) 在对准时，选取2个不同的时刻t1和t2，可以得到
(11) 将式(11)写成矩阵的形式可得
(12) 对式(12)作进一步的变形可得到Cib0i0的具体表达为
(13) 值得注意的是，为了求得Cib0i0，要求Vi0(t1)与Vi0(t2)不平行，为了满足这一要求，在对准时，载体只需做一转弯运动，即要求航向角有明显的变化，将t1和t2分别取为转弯前的某一时刻和转弯后的某一时刻；同时，为了减小测量速度误差的影响，要求载体在t1和t2时刻具有较快的运行速度，对其他时间段的运行速度不作要求。
综上可知，行进间初始对准算法中将捷联矩阵Cbn(t)的求解分解成Ci0n(t)、Cbib0(t)和Cib0i03个矩阵乘积的形式，这3个矩阵分别由式(4)、式(7)和式(13)求得，最后将求得的结果代入式(1)，便可求得初始姿态矩阵Cbn(t)，完成初始对准。
3. 误差分析
3.1 误差分析方法1
对式(1)两端取微分，可得
(14) 由式(14)可知，对准算法的误差由3部分组成，由Ci0n(t)的表达式(4)可知，Ci0n(t)的值由对准开始时刻的经度和纬度、当前时刻的经度和纬度以及对准时间所决定，而经度由GPS实时提供，认为是准确的，那么由Ci0n(t)带来的误差可以被忽略，即
(15) 由δCbib0(t)引起的误差[24]为
(16) 式中：Φib0为ib0系的失准角(计算坐标系相对真实坐标系的误差角)。由于εb很小，本文中采用低精度的陀螺，其常值漂移为0.1(°)/h，与转弯时的角速度(通常在10(°)/s)相比，完全可以忽略，又因对准时间一般较短，所以由εb引起的误差可以忽略不计，即
(17) 接下来主要分析Cib0i0引起的姿态角误差，由Cib0i0的求解过程可知，Cib0i0是由Vn(t)、Vb(t)、Ci0n(t) 和Cbib0(t)共同决定的，由式(16)和式(17)可知Ci0n(t)和Cbib0(t)可以认为是准确的，如果直接分析由Vn(t)和Vb(t)的误差引起的Cib0i0的误差，进而分析由Cib0i0的误差引起的姿态角误差比较困难，但可以从Vn(t)、Vb(t)以及姿态角Φ=[θ γ φ]T之间的关系来分析由Vn(t)和Vb(t)的误差引起的姿态角误差，其中θ、γ和φ分别为俯仰角、横滚角和航向角。Vn(t)、Vb(t)和姿态角Φ之间的关系为
(18) 由式(18)可得
(19) 对式(19)两端求微分可得式(20)。
(20) 式中：d(·) 为增量，也就是误差，将式(18)代入式(20)并进行整理，可得
(21) 对于陆用惯导系统，由于对准时间比较短，可认为对准过程中的俯仰角约为0°且保持不变，则式(21)可进一步化解为
(22) 3.2 误差分析方法2
为了获得误差方程，Cib0i0的表达式需要被改写为另一种形式，根据正交矩阵的性质，由式(13)可得
(23) 其中：
取t2 时刻为对准结束时刻t ，将式(23)代入式(1)可得
(24) 式中：
由于对准的时间比较短，因而载车在t1 时刻的位置和在t2 时刻的位置的经纬度基本相等，所以关系式(25)成立。
(25) 根据式(25)，进一步可得
(26) 在对准过程中，俯仰角和横滚角可近似为0°，假设载车从t1 时刻到t2 时刻转过的角度为α，从而可得
(27) 根据式(27)可得
(28) 将式(26)和式(28)代入式(24)可得
(29) 由姿态角和矩阵Cbnt2 之间的关系可得
(30) 式中：TMN为矩阵Cbn(t2)中第M行第N列的元素。用式(19)推导式(22)的方法可得姿态角的误差方程为
(31) 比较式(22)和式(31)可以发现，2种误差分析方法所得到的俯仰角和航向角的误差表达式是相同的，这也相互印证了2种方法的合理性。
根据式(31)还可以明确转弯角度、最小行驶速度及速度误差对姿态角误差的影响，很明显，在GPS和里程计的测速误差确定的条件下，行驶速度越快，姿态角误差越小，如果知道允许的最大姿态角误差，便可以求得最小的运行速度；转弯角度不能太小，如果想知道在行驶速度和器件误差确定的条件下，转弯角度为多少度时，横滚角误差最小，可通过对横滚角误差方程求极值的方法获得。
由式(31)可知，GPS的测速误差、载车的运行速度是引起姿态角误差的主要原因。当载车以25 m/s的速度运行，GPS的测速误差为0.1 m/s，对准过程中载车转过90°的弯，即航向角由0°变为 90°时，俯仰角的误差为dθ =0.229 2°，横滚角的误差为dγ=-0.229 2°，航向角的误差为dφ=-0.229 2°。
4. 仿真实验与分析
4.1 仿真条件设置
本文提出的对准算法要求载车在对准过程有一次转弯运动，所以设计载车的运行路线为：载车先以25 m/s 的速度沿北向做直线运动，5 s之后开始减速为转弯运动做准备，经过5 s的减速运动后，以 2 m/s 的速度转弯，经过20 s后转过90°，此时载车的速度方向指向西，然后载车做5 s的加速运动，在第35 s时载车的速度达到25 m/s,之后载车以此速度做45 s的匀速直线运动。
开始对准时的经度为λ0=116.343 4°，纬度为L0=39.977 8°，初始的姿态角为Φ0=[0 0 0]T，低精度陀螺仪的采样率设为100 Hz，GPS和里程计的更新率为1 Hz，里程计的测量误差为行驶里程的千分之一，并将其转化为速度误差，GPS、里程计和陀螺仪的误差如表 1所示，表中的随机误差为白噪声误差。在仿真时，将t1取为1 s，t2取为t(t≥35 s)。
表 1 传感器误差设置Table 1. Sensor errors setting传感器误差 常值偏移 随机误差 陀螺仪误差/((°)·h-1) 0.1 0.01 东向速度GPS误差/(m·s-1) 0.1 0.01 北向速度GPS误差/(m·s-1) 0.1 0.01 天向速度GPS误差/(m·s-1) 0.1 0.01 里程计误差/(m·s-1) 0.05 0.005 4.2 仿真结果与分析
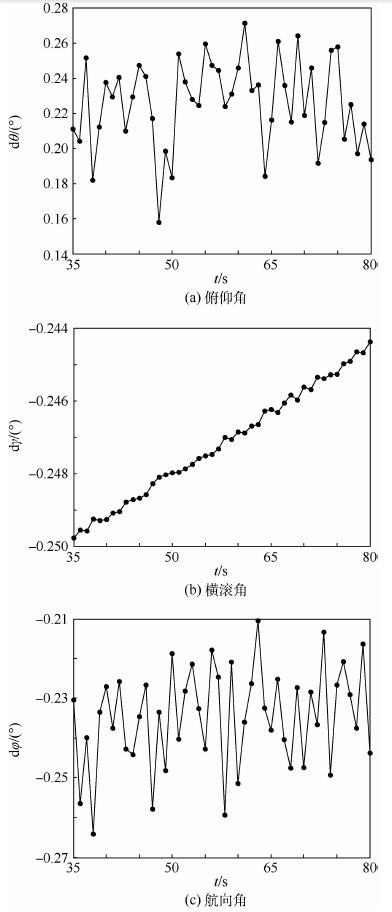
图 1是俯仰角、横滚角和航向角在第35 s到第80 s之间的误差曲线，图中的圆点表示解算得到的姿态角误差，表 2 是相应的误差统计数据。由图可知，经过35 s便可完成对准，对准时间比较短而且对准误差小于0.3°，满足粗对准的要求。
图 1 俯仰角误差、横滚角误差及偏航角误差曲线Figure 1. Alignment errors for pitch angle，roll angle and yaw angle表 2 误差统计数据Table 2. Statistics of alignment errors姿态角 误差均值/(°) 误差标准差/(°) 俯仰角 0.225 8 0.025 2 横滚角 -0.247 2 0.001 6 航向角 -0.234 6 0.012 6 由表 2可知，俯仰角和航向角的误差均值分别为0.225 8°和-0.234 6°，与由误差方程计算得到的俯仰角和航向角误差0.229 2°和-0.229 2°相比，分别相差-0.003 4°和-0.005 4°，说明上面推导的误差方程是合理的。由图 1(a) 和图 1(c)还可以发现，俯仰角和航向角的误差存在小幅度的波动现象，由式(21)可知，这主要是由表 1中GPS的随机误差引起的，这也是造成解算得到的误差与由误差方程计算得到的误差存在差异的主要原因。由式(31)可知，在转弯角为90°，时，横滚角的误差主要由t1 时刻GPS的天向速度误差和运行速度决定，仿真时t1 时刻的速度误差为0.108 7m/s(常值误差与随机误差的和)，由式(31)计算得到的横滚角误差为-0.249 1°，与表 2中的误差均值-0.247 2°相差-0.001 9°说明误差方程是可信的。由图 1(b)横滚角的误差曲线可知，其值由-0.249°变到-0.244°，变化量为0.005°，与误差值相比可以忽略，且其在变化过程中也并非严格的在数值上递减，所以可以认为在转弯角为90°时，横滚角误差保持不变。
由图 1(b)中横滚角的误差变化曲线可知，在转弯角为90°时，横滚角的误差几乎没有波动，说明与俯仰角和航向角相比，受随机误差的影响比较小，这一结论同样可由表 2中的误差标准差说明；另一方面，由式(31)可知，俯仰角和航向角误差主要受t2 时刻速度误差的影响，而横滚角误差主要受t1 时刻速度误差的影响，由于t2是变化的，t1 是保持不变的，这也能说明为什么横滚角受随机误差的影响比较小。
尽管在误差方程中没有体现出里程计误差对姿态角误差的影响，但测量得到的载车在b 系的速度并非载车的真实速度，而是包含了里程计测量误差的速度，所以在对准过程中里程计的测量误差已经对姿态角的误差产生了作用。
2种误差分析方法中都假定了俯仰角和横滚角为0°，同时再考虑计算误差和舍入误差等的影响，必然使得由误差方程计算得到的误差与通过仿真得到的误差之间存在微小的差异。
5. 结 论
针对车载捷联惯导系统，提出一种快速行进间粗对准方法，根据理论分析和仿真实验可以得出如下结论：
1) 该行进间对准方法能在1min之内完成粗对准，采用0.1(°)/h的低精度陀螺，对准误差小于0.3°。
2) 姿态角误差主要受GSP提供的速度的常值误差的影响，且载车的运行速度越快，姿态角误差越小。
3) 与现有的对准方法相比，该方法没有用到加速度计的测量信息，这使得该方法只能在行进间完成对准；与现有的行进间对准方法相比，该方法对载车的机动方式没有过多的限制，且可以快速完成粗对准。
本文中用2种方法给出了姿态角的误差方程，接下来会在此基础上对该算法进行改进，提高对准的精度；同时研究如何将该方法与现有的滤波方法相结合，以期获得一种对准精度高且对准时间短的行进间对准方法。
-
图 14 减速器与传动机构子模块简图
Figure 14. Simplified diagram of reducer and transmissionmechanism submodule
图 22 舵机模型指令信号与响应对比
Figure 22. Comparison of command signal and response of actuator model
图 24 线性航机输出轴的响应(43~44.5 Hz)
Figure 24. Response of linear actuator output shaft (43~44.5 Hz)
图 26 线性航机输出轴的响应(98~99.5 Hz)
Figure 26. Response of linear actuator output shaft (98~99.5 Hz)
图 28 非线性舵机输出轴的响应(43~44.5 Hz)
Figure 28. Response of nonlinear actuator outputshaft (43~44.5 Hz)
图 29 非线性舵机输出轴的响应(98~99.5 Hz)
Figure 29. Response of nonlinear actuator outputshaft (98~99.5 Hz)
图 38 舵机仅包含间隙时激励幅值对动刚度的影响
Figure 38. Influence of excitation amplitude on dynamic stiffness of outuator with freeplay only
图 45 舵机仅包含摩擦时激励幅值对动刚度的影响
Figure 45. Influence of excitation amplitude on dynamic stiffness of outuator with friction only
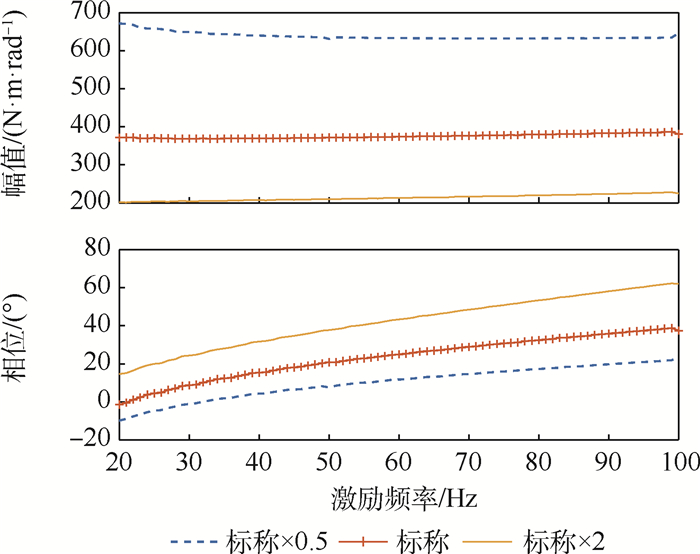
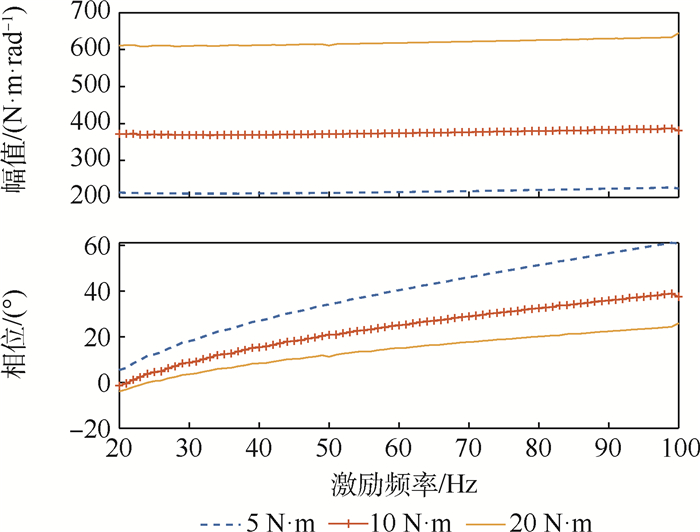
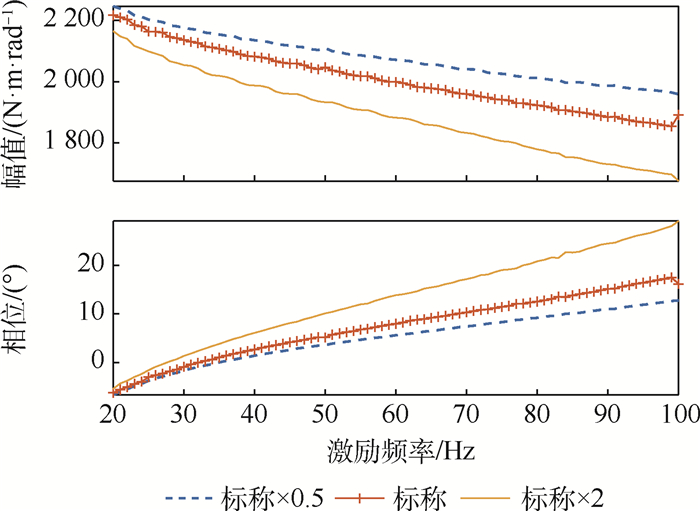
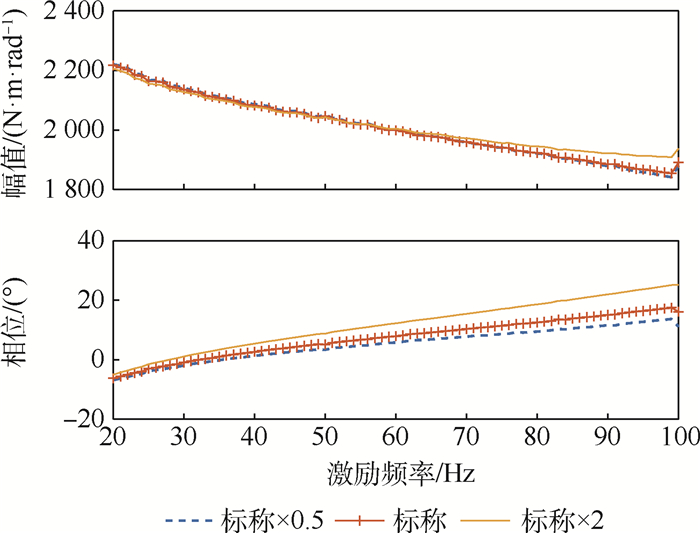
参数 数值 电感L/mH 6.53×10-4 电阻R/Ω 1.1 力矩系数Km/(N·m·A-1) 0.024 反电动势系数Ce/(V·s·rad-1) 0.034 电机转子转动惯量Jm/(kg·m2) 1.09×10-6 电机转子黏性阻尼系数bm 0.003 电机与减速器连接刚度km/(N·m·rad-1) 1 000 小齿轮转动惯量J1/(kg·m2) 2.4×10-8 大齿轮转动惯量J2/(kg·m2) 4×10-6 小齿轮半径r1/m 0.005 大齿轮半径r2/m 0.022 5 齿轮啮合刚度kg/(kg·s2·rad-1) 108 齿轮与传动机构连接刚度kz/(N·m·rad-1) 1 000 滚珠丝杠转动惯量Jsg/(kg·m2) 1.12×10-5 滚珠丝杠螺旋角λ/(°) 6.06 滚珠丝杠半径rsg/m 0.006 滚珠丝杠效率η 0.85 拨叉长度Lbc/m 0.028 5 输出轴转动惯量Jshaft/(kg·m2) 4.1×10-5 接触刚度Kjc 6×10-6 间隙半宽度dfp/rad 0.000 5 库伦摩擦参数Fc/N 1 静摩擦系数Fs/N 1.5 动态摩擦参数σ0/(N·s·m-1) 105 切换速度Vs/(m·s-1) 0.001 动态摩擦参数σ1/(N·s·m-1) 316.23 黏性阻尼参数σ2/(N·s·m-1) 0.4 
下载: 导出CSV
表 2 舵机参数对动刚度的影响
Table 2. Influence of actuator parameters on dynamic stiffness
参数 影响程度 幅值关系 相位关系 线圈电感 小 ↓ — 电阻 小 ↑ — 力矩系数 大 — — 反电动势系数 很小 — — 电机转子转动惯量 大 ↓ ↓ 电机转子黏性阻尼系数 大 ↓ ↑ 小齿轮转动惯量 很小 — — 大齿轮转动惯量 很小 — — 小齿轮半径 大 ↑ ↑ 大齿轮半径 大 ↓ ↓ 齿轮啮合刚度 很小 — — 齿轮与传动机构连接刚度 很小 ↑ — 滚珠丝杠转动惯量 小 ↓ ↓ 滚珠丝杠半径 大 ↑ ↑ 滚珠丝杠效率 大 ↓ ↓ 拨叉长度 很大 ↑ ↓ 输出轴滚珠惯量 小 ↓ ↑ 输出轴阻尼 很大 ↑ ↑
下载: 导出CSV
-
[1] LYSHEVSKI S E. Electromechanical flight actuators for advanced flight vehicles[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 511-518. doi: 10.1109/7.766933 [2] 郭雪梅, 贾宏光, 冯长有. 直流无刷电机位置跟踪的模糊PID控制[J]. 长春理工大学学报(自然科学版), 2008, 31(1): 99-103.GUO X M, JIA H G, FENG C Y. Fuzzy PID control of brushless DC motor position tracking[J]. Journal of Changchun University of Science and Technology(Natural Science Edition), 2008, 31(1): 99-103(in Chinese). [3] 钟晓伟, 宋蛰存, 姜忠. 模糊PID控制器在无刷直流电机控制系统中的应用[J]. 化工自动化及仪表, 2010, 37(8): 87-89.ZHONG X W, SONG Z C, JIANG Z. Application of fuzzy PID controller for BLDCM control system[J]. Control and Instruments in Chemical Industry, 2010, 37(8): 87-89(in Chinese). [4] 张新榃, 吴志刚, 杨超. 考虑舵机动力学的舵系统颤振特性分析[J]. 北京航空航天大学学报, 2011, 37(8): 927-932. https://bhxb.buaa.edu.cn/CN/abstract/abstract12035.shtmlZHANG X T, WU Z G, YANG C. Flutter analysis for rudder considering actuator's dynamics[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(8): 927-932(in Chinese). https://bhxb.buaa.edu.cn/CN/abstract/abstract12035.shtml [5] KIM S H, TAHK M J. Dynamic stiffness transfer function of an electromechanical actuator using system identification[J]. International Journal of Aeronautical and Space Sciences, 2018, 19(1): 208-216. doi: 10.1007/s42405-018-0005-7 [6] ZHANG R, WU Z, YANG C. Dynamic stiffness testing-based flutter analysis of a fin with an actuator[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1400-1407. doi: 10.1016/j.cja.2015.08.016 [7] WANG Y, MEGLI T, HAGHGOOIE M, et al. Modeling and control of electromechanical valve actuator: 2002-01-1106[R]. Michigan: SAE, 2002. [8] 刘敏, 刘藻珍, 王金柱. 某型电动舵机建模与仿真研究[J]. 弹箭与制导学报, 2004, 24(3): 123-125.LIU M, LIU Z Z, WANG J Z. Modeling and simulation researeh of a electromechanical actuator[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004, 24(3): 123-125(in Chinese). [9] 张奎轩, 曾庆华. 面向故障仿真的舵机系统建模方法研究[J]. 航空计算技术, 2015, 45(3): 95-98.ZHANG K X, ZENG Q H. Research on circuit simulation method for actuator system[J]. Aeronautical Computing Technique, 2015, 45(3): 95-98(in Chinese). [10] 张开敏, 邓瑞清. 舵机传动机构动力学建模与分析[J]. 航空兵器, 2012(4): 34-37.ZHANG K M, DENG R Q. Dynamical modeling and analysis of actuator transmission system[J]. Aero Weaponry, 2012(4): 34-37(in Chinese). [11] 黎海青, 郭百巍, 徐红. 基于ADAMS与SIMULINK的舵机虚拟样机建模和仿真[J]. 系统仿真学报, 2009, 21(21): 6886-6888.LI H Q, QUO B W, XU H. Virtual prototype modeling and simulation analysis of servo based on ADAMS and SIMULINK[J]. Journal of System Simulation, 2009, 21(21): 6886-6888(in Chinese). [12] BEIER T. Prediction and measurement of the dynamic stiffness and damping of hydraulic servo-actuators[C]//18th Structural Dynamics and Materials Conference. Reston: AIAA, 1977: 107-116. [13] BLAIGNAN V B, SKORMIN V A. Stiffness enhancement of flight control actuator[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(2): 380-390. [14] THOMPSON D F, PRUYN J S, SHUKLA A. Feedback design for robust tracking and robust stiffness in flight control actuators using a modified QFT technique[J]. International Journal of Control, 1999, 72(16): 1480-1497. doi: 10.1080/002071799220128 [15] BALLESTEROS H M S, DAS NEVES CALVO R, ADADE FILHO A. Dynamic stiffness enhancement of a flight control actuator using control techniques[C]//2017 IEEE International Conference on Mechatronics. Piscataway: IEEE Press, 2017: 260-265. [16] SHIN W H, LEE I, SHIN Y S, et al. Nonlinear aeroelastic analysis for a control fin with an actuator[J]. Journal of Aircraft, 2007, 44(2): 597-605. [17] 张仁嘉, 吴志刚, 杨超. 电动伺服舵系统动力学建模及颤振分析[J]. 北京航空航天大学学报, 2016, 42(7): 1368-1376. doi: 10.13700/j.bh.1001-5965.2015.0448ZHANG R J, WU Z G, YANG C. Dynamic modeling and flutter analysis of a fin-actuator system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1368-1376(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0448 [18] CROKE S, HERRENSCHMIDT J. More electric initiative-power-by-wire actuation alternatives[C]//Proceedings of the National Aerospace and Electronics Conference. Piscataway: IEEE Press, 1994: 1338-1346. [19] XIAO H, BRENNAN M J, SHAO Y. On the undamped free vibration of a mass interacting with a Hertzian contact stiffness[J]. Mechanics Research Communications, 2011, 38(8): 560-564. [20] 杨珍书. 飞控机电作动系统非线性建模和故障分析[D]. 天津: 中国民航大学, 2018: 33-34.YANG Z S. Nonlinear modeling and fault analysis of flight control electromechanical actuation system[D]. Tianjin: Civil Aviation University of China, 2018: 33-34(in Chinese). [21] 周金柱, 段宝岩, 黄进. LuGre摩擦模型对伺服系统的影响与补偿[J]. 控制理论与应用, 2008, 25(6): 990-994.ZHOU J Z, DUAN B Y, HUANG J. Effect and compensation for servo systems using LuGre friction model[J]. Control Theory & Applications, 2008, 25(6): 990-994(in Chinese). [22] CANUDAS D W C, OLSSON H, ASTROM K J, et al. A new model for control of systems with friction[J]. IEEE Transactions on Automatic Control, 1995, 40(3): 419-425. [23] 张仁嘉. 飞行器气动伺服弹性若干关键问题研究[D]. 北京: 北京航空航天大学, 2015: 33-34.ZHANG R J. Extensional research on several critical aeroservoelastic problems of air vehicles[D]. Beijing: Beihang University, 2015: 33-34(in Chinese). 期刊类型引用(4)
1. 魏正桓，唐万春，李保珠，孙芮. 一种基于起伏地形与辐射电场分布相似性的指纹辅助定位方法仿真研究. 电波科学学报. 2021(05): 737-746 . 
百度学术2. 德庆措姆. 西藏那曲市雷电防护工作中的电磁辐射污染抑制方法研究. 环境科学与管理. 2019(10): 140-144 . 百度学术3. 沈步楼. 辐射干扰下混合动力汽车低频电磁辐射抑制方法. 环境技术. 2018(05): 35-40 . 百度学术4. 刘卫东，刘尚合. 基于峰度特征的瞬态电磁信号检测提取方法. 微波学报. 2018(06): 78-83 . 百度学术其他类型引用(4)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 1114
- HTML全文浏览量: 380
- PDF下载量: 227
- 被引次数: 8
