距离相关系数融合GPR模型的卫星异常检测方法

孙宇豪; 李国通; 张鸽

doi:10.13700/j.bh.1001-5965.2020.0041

距离相关系数融合GPR模型的卫星异常检测方法

doi: 10.13700/j.bh.1001-5965.2020.0041

孙宇豪^{1, 2},
李国通^{1, 2, 3, ,},
张鸽^{1, 2}

1.
中国科学院微小卫星创新研究院, 上海 201203
2.
中国科学院大学, 北京 100049
3.
上海科技大学信息科学与技术学院, 上海 201210

基金项目:

上海市科学技术委员会科研计划 17DZ1100700

详细信息

作者简介:
孙宇豪  女, 硕士研究生。主要研究方向: 卫星异常检测技术

李国通  男, 博士, 研究员, 博士生导师。主要研究方向: 卫星导航与定位技术、信号检测和识别技术

张鸽   男, 博士研究生。主要研究方向: 卫星自主健康管理技术

通讯作者:
李国通, E-mail: ligt@microsate.com

中图分类号: V557⁺.3;TN911.71
计量
- 文章访问数: 744
- HTML全文浏览量: 232
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2020-02-17
- 录用日期: 2020-04-17
- 网络出版日期: 2021-04-20

A satellite anomaly detection method based on distance correlation coefficient and GPR model

SUN Yuhao^{1, 2},
LI Guotong^{1, 2, 3
, ,},
ZHANG Ge^{1, 2}

1.
Innovation Academy for Microsatellite of CAS, Shanghai 201203, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
School of Information Science and Technology, ShanghaiTech University, Shanghai 201210, China

Funds:

Scientific Research Plan of Shanghai Science and Technology Commission 17DZ1100700

More Information

Corresponding author: LI Guotong, E-mail: ligt@microsate.com

摘要

摘要:
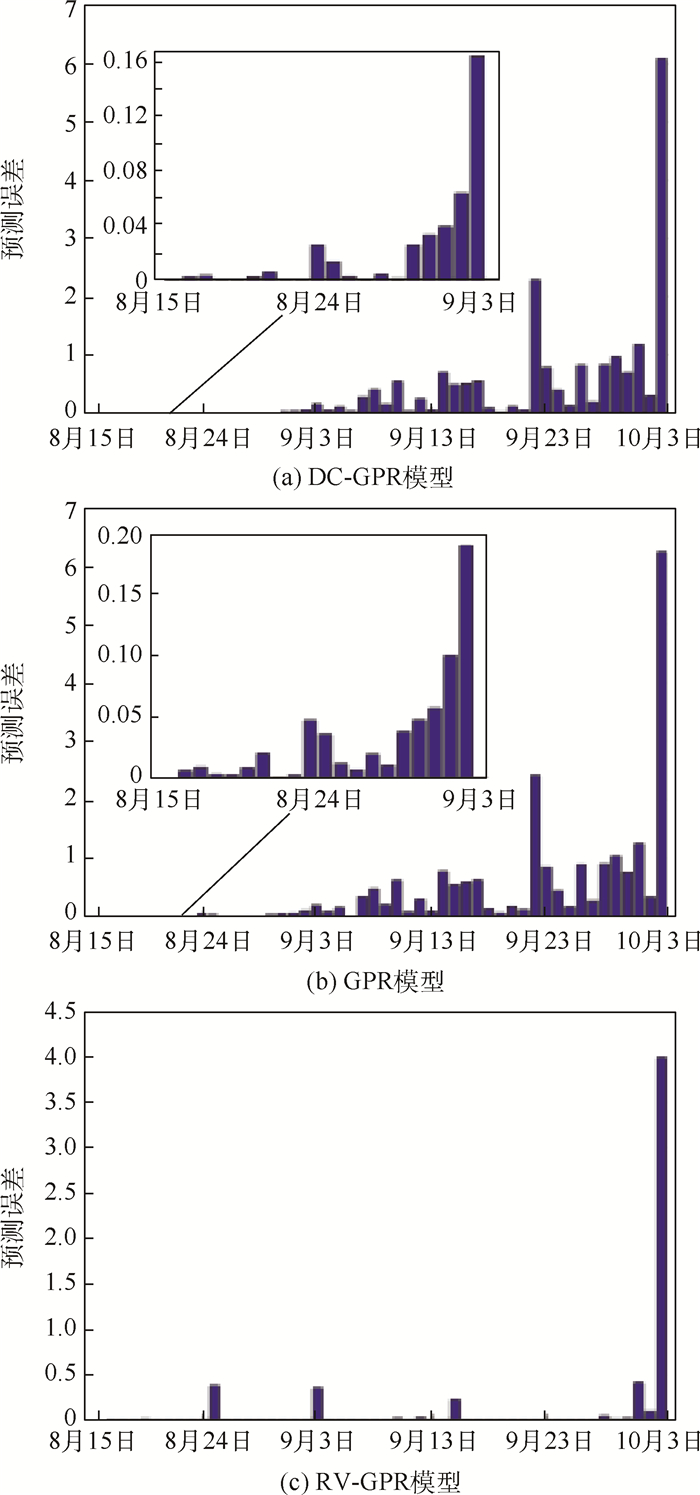
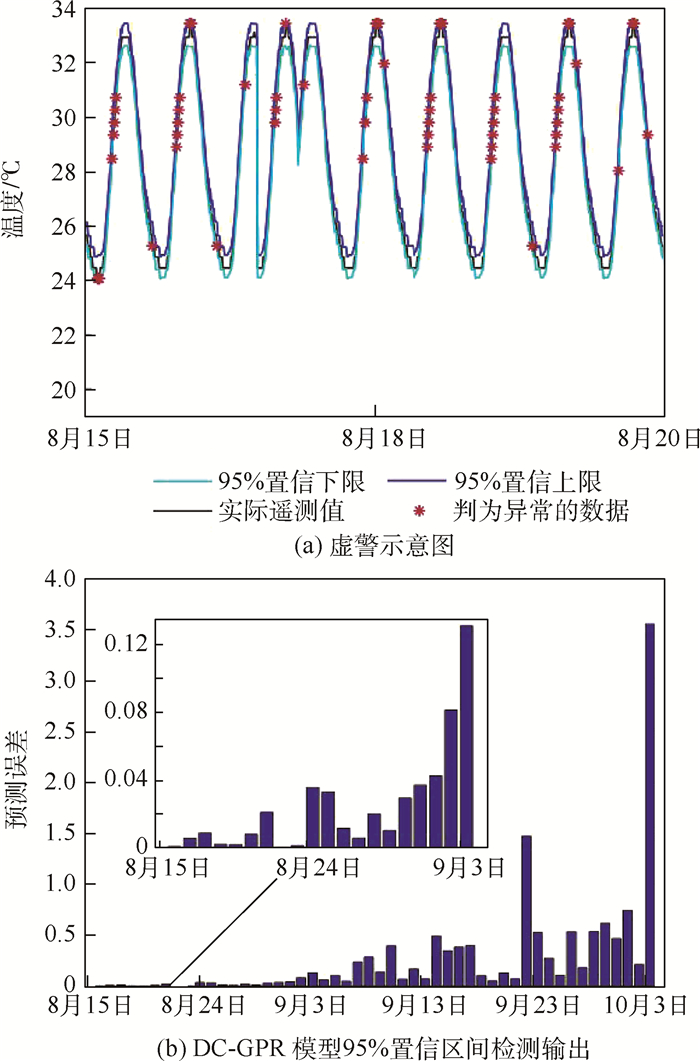
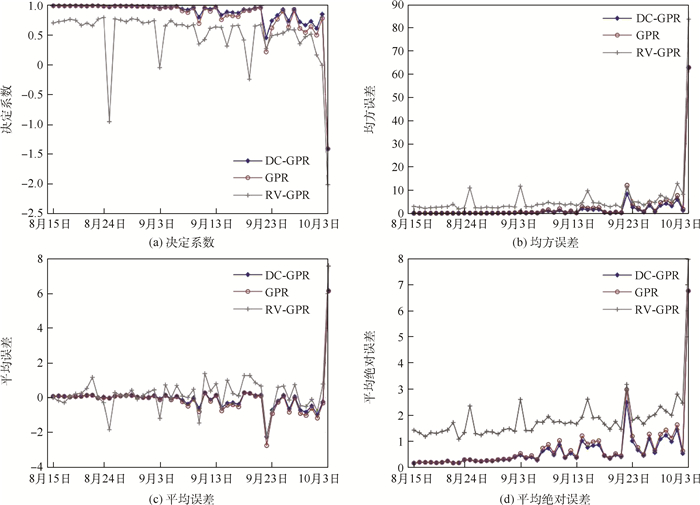
卫星在轨运行期间，遥测数据表现形式通常为多维时间序列。高斯过程回归(GPR)模型可以为重要的遥测参数提供动态门限，及时发现隐藏在工程阈值内的故障征兆，但是高维卫星数据使得GPR模型具有局限性。因此，为获取与多个遥测参数相关的动态门限，在GPR模型的基础上，融合距离相关系数对预测变量进行选择，减少信息冗余和计算量，提高模型的可解释性，并估计模型的泛化误差以设置更合理的预测区间，提高模型的泛化能力，检测数据流的持续异常。对实际在轨卫星数据进行仿真实验，验证了距离相关系数融合GPR模型的卫星异常检测方法可以在卫星故障早期检测到数据异常，而且提高了模型的预测性能，降低了虚警率。
- 卫星异常检测 /
- 高斯过程回归(GPR) /
- 距离相关系数 /
- 变量选择 /
- 泛化误差
Abstract:
During the orbital operation of the satellite, the telemetry data is usually represented by multidimensional time series. The Gaussian Process Regression (GPR) model can provide dynamic thresholds for important telemetry parameters and timely discover failure symptoms hidden within the engineering threshold. However, high dimensional satellite data makes GPR model limited. Therefore, in order to obtain the dynamic threshold related to multiple telemetry parameters, based on the GPR model, the distance correlation coefficient is combined to select predictive variables, reduce the information redundancy and the amount of calculation, and improve the interpretability of the model.The generalization error of the model is estimated to set a more reasonable prediction interval, to improve the generalization ability and detect the continuous abnormality of the data stream. Simulation experiments on actual orbiting satellite data verify that this method can detect data anomalies in the early failure of the satellite, improve the prediction performance of the model and reduce the false alarm rate.
- satellite anomaly detection /
- Gaussian Process Regression (GPR) /
- distance correlation coefficient /
- variable selection /
- generalization error

HTML全文

图 1 过拟合模型的检测结果

Figure 1. Detection results of overfitting model

下载: 全尺寸图片幻灯片

图 2 基于DC-GPR模型的异常检测流程

Figure 2. Flowchart of anomaly detection based on DC-GPR model

下载: 全尺寸图片幻灯片

图 3 故障相关单机的遥测参数

Figure 3. Telemetry parameters of a fault-related machine

下载: 全尺寸图片幻灯片

图 4 不同遥测参数与响应变量间的距离相关系数

Figure 4. Distance correlation coefficient between each telemetry parameter and response variable

下载: 全尺寸图片幻灯片

图 5 不同模型的检测结果

Figure 5. Detection results of different models

下载: 全尺寸图片幻灯片

图 6 DC-GPR模型95%置信区间检测结果

Figure 6. Detection results of DC-GPR 95% confidence interval

下载: 全尺寸图片幻灯片

图 7 不同模型的性能指标对比

Figure 7. Comparison of performance indices of different models

下载: 全尺寸图片幻灯片

图 8 异常时不同遥测参数与响应变量间的距离相关系数

Figure 8. Distance correlation coefficient between each telemetry parameter and response variable during anomalies

下载: 全尺寸图片幻灯片

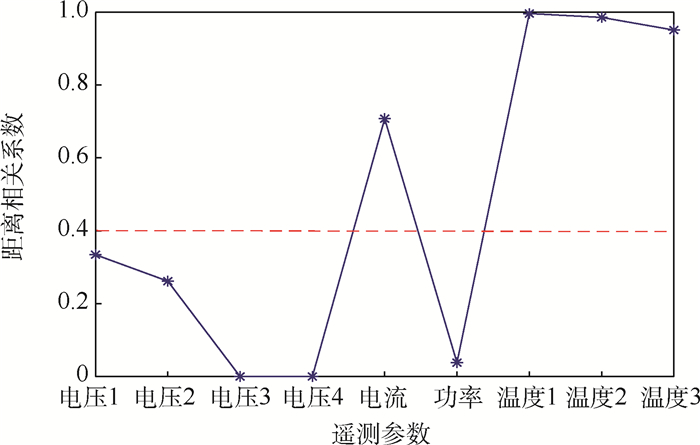
表 1 相关程度度量

Table 1. Relevance measure

相关性	距离相关系数
极强相关	0.8~1.0
强相关	0.6~0.8
中相关	0.4~0.6
弱相关	0.2~0.4
极弱或无相关	0~0.2

下载: 导出CSV

表 2 不同模型的检测评估

Table 2. Detection evaluation of different models

模型	DR/%	FA/%	MA/%
DC-GPR	86.67	5.41	0
DC-GPR(95%置信区间)	52.94	19.51	0
GPR	60	14.63	0
RV-GPR	86.67	11.76	57.14

下载: 导出CSV

参考文献(31)

[1]	BELCASTRO C M.Aviation safety program: Integrated vehicle health management technical plan summary[R].Washington, D.C.: NASA Technology Report, 2006.
[2]	彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述[J]. 仪器仪表学报, 2016, 37(9): 1929-1945. doi: 10.3969/j.issn.0254-3087.2016.09.003 PENG X Y, PANG J Y, PENG Y, et al. Review on anomaly detection of spacecraft telemetry data[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1929-1945(in Chinese). doi: 10.3969/j.issn.0254-3087.2016.09.003
[3]	CHANDOLA V, BANERJEE A, KUMAR V.Anomaly detection: A survey[J]. ACM Computing Surveys, 2009, 41(3): 1-58. http://search.ebscohost.com/login.aspx?direct=true&db=buh&AN=43479988&site=ehost-live
[4]	张克明, 蔡远文, 任元. 基于生成对抗网络的航天异常事件检测方法[J]. 北京航空航天大学学报, 2019, 45(7): 1329-1336. doi: 10.13700/j.bh.1001-5965.2018.0682 ZHANG K M, CAI Y W, REN Y.Space anomaly events detection approach based on generative adversarial nets[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(7): 1329-1336(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0682
[5]	吕军晖, 周刚, 金毅. 一种基于时间序列的自适应网络异常检测算法[J]. 北京航空航天大学学报, 2009, 35(5): 636-639. https://bhxb.buaa.edu.cn/CN/Y2009/V35/I5/636 LÜ J H, ZHOU G, JIN Y.Adaptive aberrant network traffic detection algorithm based on time series forecast[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(5): 636-639(in Chinese). https://bhxb.buaa.edu.cn/CN/Y2009/V35/I5/636
[6]	张妮, 车立志, 吴小进. 基于数据驱动的故障诊断技术研究现状及展望[J]. 计算机科学, 2017, 44(6A): 37-42. doi: 10.11896/j.issn.1002-137X.2017.6A.008 ZHANG N, CHE L Z, WU X J.Present situation and prospect of data-driven based fault diagnosis technique[J]. Computer Science, 2017, 44(6A): 37-42(in Chinese). doi: 10.11896/j.issn.1002-137X.2017.6A.008
[7]	彭宇, 刘大同. 数据驱动故障预测和健康管理综述[J]. 仪器仪表学报, 2014, 35(3): 481-495. https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201403001.htm PENG Y, LIU D T.Data-driven prognostics and health management: A review of recent advances[J]. Chinese Journal of Scientific Instrument, 2014, 35(3): 481-495(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201403001.htm
[8]	AZEVEDO D R, AMBROSIO A M, VIEIRA M, et al.Applyingdata mining for detecting anomalies in satellites[C]//European Dependable Computing Conference, 2012: 212-217.
[9]	HAWKINS S, HE H, WILLIAMS G J, et al.Outlier detection using replicator neural networks[C]//International Conference on Data Warehousing and Knowledge Discovery.Berlin: Springer, 2002: 170-180.
[10]	WILLIAMS G, BAXTER R, HE H, et al.A comparative study of RNN for outlier detection in data mining[C]//IEEE International Conference on Data Mining.Piscataway: IEEE Press, 2002: 709-712.
[11]	SCHOLKOPF B, PLATT J C, SHAWE T J, et al. Estimating the support of a high-dimensional distribution[J]. Neural Computation, 2014, 13(7): 1443-1471. http://www.ncbi.nlm.nih.gov/pubmed/11440593
[12]	DAS K, BHADURI K, VOTAVA P, et al. Distributed anomaly detection using 1-class SVM for vertically partitioned data[J]. Statistical Analysis and Data Mining, 2011, 4(4): 393-406. doi: 10.1002/sam.10125
[13]	ANAISSI A, KHO N L, WANG Y, et al. Automated parameter tuning in one-class support vector machine: An application for damage detection[J]. Journal of Data Science, 2018, 6(4): 311-325. doi: 10.1007/s41060-018-0151-9
[14]	ESTER M.A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996: 226-231.
[15]	RAMASWAMY S, RASTOGI R, SHIM K, et al. Efficient algorithms for mining outliers from large data sets[J]. International Conference on Management of Data, 2000, 29(2): 427-438.
[16]	YIN C, ZHANG S, YIN Z, et al. Anomaly detection model based on data stream clustering[J]. Cluster Computing, 2019, 22(1): 1729-1738. doi: 10.1007/s10586-017-1066-2
[17]	ALGULIYEV R M, ALIGULIYEV R M, SUKHOSTAT L, et al. Anomaly detection in big data based on clustering[J]. Statistics, Optimizationand Information Computing, 2017, 5(4): 325-340. http://www.researchgate.net/publication/321448608_Anomaly_Detection_in_Big_Data_based_on_Clustering/download
[18]	QIU H, EKLUND N H, HU X, et al.Anomaly detection using data clustering and neural networks[C]//International Joint Conference on Neural Network, 2008: 3627-3633.
[19]	AGGARWAL C C, YU P S.Outlier detection with uncertain data[C]//SIAM International Conference on Data Mining, 2008: 483-493.
[20]	THATTE G, MITRA U, HEIDEMANN J, et al. Parametric methods for anomaly detection in aggregate traffic[J]. IEEE ACM Transactions on Networking, 2011, 19(2): 512-525. doi: 10.1109/TNET.2010.2070845
[21]	PATCHA A, PARK J.An overview of anomaly detection techniques: Existing solutions and latest technological trends[J]. Computer Networks, 2007, 51(12): 3448-3470. doi: 10.1016/j.comnet.2007.02.001
[22]	PAN D W, LIU D T, ZHOU J, et al. Anomaly detection for satellite power subsystem with associated rules based on kernel principal component analysis[J]. Microelectronics Reliability, 2015, 55(9): 2082-2086. http://www.sciencedirect.com/science/article/pii/S0026271415300949
[23]	COHEN G, HILARIO M, PELLEGRINI C, et al. One-class support vector machines with a conformal kernel. A case study in handling class imbalance[J]. Lecture Notes in Computer Science, 2004, 3138: 850-858. doi: 10.1007/978-3-540-27868-9_93
[24]	TARIQ S, LEE S, SHIN Y, et al.Detecting anomalies in space using multivariate convolutional LSTM with mixtures of probabilistic PCA[C]//Knowledge Discovery and Data Mining, 2019: 2123-2133.
[25]	DONG D.Mine gas emission prediction based on Gaussian process model[J]. Procedia Engineering, 2012, 45: 334-338. doi: 10.1016/j.proeng.2012.08.167
[26]	ANOGARAN G, LOPEZ D.A Gaussian process based big data processing framework in cluster computing environment[J]. Cluster Computing, 2018, 21(1): 189-204. doi: 10.1007/s10586-017-0982-5
[27]	SZEKELY G J, RIZZO M L, BAKIROV N K, et al. Measuring and testing dependence by correlation of distances[J]. Annals of Statistics, 2007, 35(6): 2769-2794. http://biomet.oxfordjournals.org/external-ref?access_num=10.1214/009053607000000505&link_type=DOI
[28]	葛芳君, 赵磊, 刘俊, 等. 基于Pearson相关系数的老年人社会支持与心理健康相关性研究的Meta分析[J]. 中国循证医学杂志, 2012, 12(11): 1320-1329. doi: 10.7507/1672-2531.20120207 GE F J, ZHAO L, LIU J, et al. Correlation between social support andmental health of the aged based on Pearson correlation coefficient: A meta-analysis[J]. Chinese Journal of Evidence-Based Medicine, 2012, 12(11): 1320-1329(in Chinese). doi: 10.7507/1672-2531.20120207
[29]	张建勇, 高冉, 胡骏, 等. 灰色关联度和Pearson相关系数的应用比较[J]. 赤峰学院学报(自然科学版), 2014, 30(11): 1-2. doi: 10.3969/j.issn.1673-260X.2014.11.001 ZHANG J Y, GAO R, HU J, et al. Application comparison of gray correlation degree and Pearson correlation coefficient[J]. Journal of Chifeng University(Natural Science Edition), 2014, 30(11): 1-2(in Chinese). doi: 10.3969/j.issn.1673-260X.2014.11.001
[30]	NADEAU C, BENGIO Y.Inference for the generalization error[J]. Neural Information Processing Systems, 1999, 52(3): 307-313. http://bioinformatics.oxfordjournals.org/external-ref?access_num=10.1023/A:1024068626366&link_type=DOI
[31]	PANG J Y, LIU D T, PENG Y, et al. Anomaly detection based on uncertainty fusion for univariate monitoring series[J]. Measurement, 2017, 95: 280-292. doi: 10.1016/j.measurement.2016.10.031