基于方位多假设的单基线干涉仪定位方法

邢怀玺; 吴华; 陈游; 张景轩

doi:10.13700/j.bh.1001-5965.2020.0074

基于方位多假设的单基线干涉仪定位方法

doi: 10.13700/j.bh.1001-5965.2020.0074

邢怀玺¹,
吴华¹,
陈游^1, ,,
张景轩²

1.
空军工程大学航空工程学院, 西安 710038
2.
合肥职业技术学院汽车工程学院, 合肥 238000

详细信息

作者简介:
邢怀玺男, 硕士研究生。主要研究方向:信息对抗理论与技术

陈游男, 博士, 讲师。主要研究方向:信息对抗理论与技术

通讯作者:
陈游, E-mail: chenyousky@163.com

中图分类号: TN971
计量
- 文章访问数: 501
- HTML全文浏览量: 102
- PDF下载量: 41
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-02
- 录用日期: 2020-06-29
- 网络出版日期: 2021-05-20

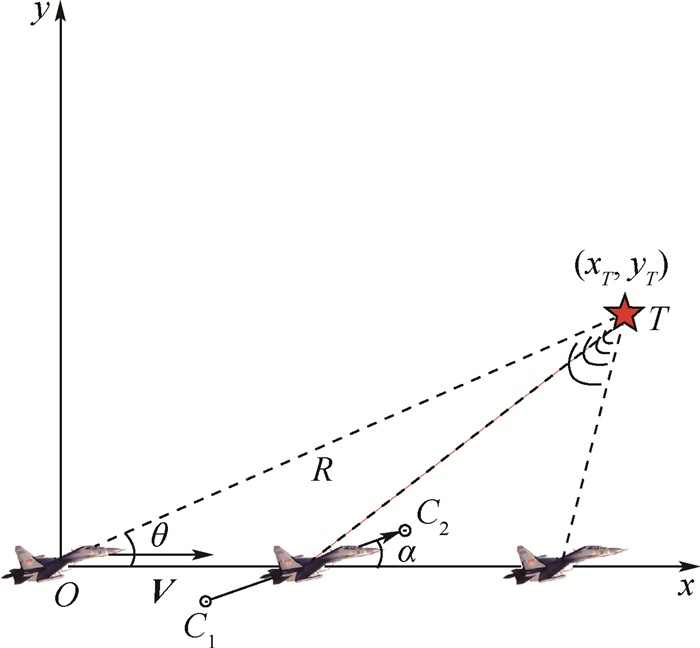
Single-baseline interferometer positioning method based on azimuth multiple hypothesis

1.
Aeronautics Engineering College, Air Force Engineering University, Xi'an 710038, China
2.
Department of Automotive Engineering, Hefei Technology College, Hefei 238000, China

More Information

Corresponding author: CHEN Y, E-mail:chenyousky@163.com

摘要

摘要:
为了解决机载单站无源定位系统中一维单基线干涉仪测量相位差信息的模糊问题，改进仅利用相位差变化率定位方法，将模糊相位差作为有效的定位参数，提出一种基于方位多假设的单基线干涉仪定位方法。利用模糊相位差和相位差变化率初始化辐射源目标的可能距离方位信息，并通过高斯-扩展卡尔曼滤波（GS-EKF）算法解算辐射源目标位置。所提方法克服了仅利用相位差变化率定位受观测平台机动影响的缺陷，有效缩短了定位时间，同时不必考虑解相位模糊，定位性能均优于仅利用相位差或相位差变化率的定位方法，在实际工程运用中可以降低设备复杂度和成本。
- 无源定位 /
- 单基线 /
- 相位差 /
- 相位差变化率 /
- 高斯-扩展卡尔曼滤波(GS-EKF)
Abstract:
In order to solve the problem of ambiguity of phase difference information measured by one-dimensional single-baseline interferometer in an airborne single-station passive positioning system, the positioning method that measures only the phase difference change rate is improved, and the fuzzy phase difference is used as an effective positioning parameter. And a single-baseline interferometer phase measurement and positioning method based on azimuth multiple hypotheses is proposed. The possible distance and azimuth information of the radiation source target is initialized using the fuzzy phase difference and the phase difference change rate, and the target location of the radiation source is solved by the Gauss-Extended Kalman Filter (GS-EKF) algorithm. This method overcomes the shortcomings of using only the phase difference change rate to locate the impact of the maneuver of the observation platform, effectively shortens the positioning time, and does not need to consider the solution of phase ambiguity. Its positioning performance is superior to the positioning method that only measures the phase difference or the phase difference change rate. In practical engineering applications, this method can reduce equipment complexity and cost.
- passive positioning /
- single baseline /
- phase difference /
- phase difference change rate /
- Gauss-Extended Kalman Filter (GS-EKF)

HTML全文

图 1 相位观测下的定位模型示意图

Figure 1. Schematic diagram of positioning model under phase observation

下载: 全尺寸图片幻灯片

图 2 模糊相位差测向及定位原理

Figure 2. Principle of direction finding and positioning based on fuzzy phase difference

下载: 全尺寸图片幻灯片

图 3 单次定位距离误差和权值更新

Figure 3. Update of distance error and weightin a single positioning

下载: 全尺寸图片幻灯片

图 4 不同初始化方位假设个数的定位性能

Figure 4. Positioning performance under different number of initial orientation assumptions

下载: 全尺寸图片幻灯片

图 5 不同观测时间下的定位结果

Figure 5. Positioning results at different observation time

下载: 全尺寸图片幻灯片

图 6 不同速度下的定位结果

Figure 6. Positioning results at different speeds

下载: 全尺寸图片幻灯片

图 7 两种方法定位性能对比

Figure 7. Comparison of positioning performance between two methods

下载: 全尺寸图片幻灯片

表 1 不同相位差误差下的定位时间(=0.5(°)/s)

Table 1. Positioning time under different phase difference measurement errors (=0.5(°)/s)

方法	定位时间/s
方法	10°	20°	30°	40°
仅测相位差	25	30	33	34
本文方法	18	18	20	21

下载: 导出CSV

表 2 不同相位差变化率误差下的定位时间(σ_φ=10(°)/s)

Table 2. Positioning time under different phase difference change rate measurement errors (σ_φ=10(°)/s)

方法	定位时间/s
方法	0.3(°)/s	0.5(°)/s	1(°)/s	2(°)/s
仅测相位差变化率	20	23	—	—
本文方法	16	18	25	—

下载: 导出CSV

参考文献(23)

[1]	田中成, 刘聪锋.无源定位技术[M].北京:国防工业出版社, 2015:374-379. TIAN Z C, LIU C F.Passive location technology[M].Beijing:National Defense Industry Press, 2015:374-379(in Chinese).
[2]	王星.航空电子对抗原理[M].北京:国防工业出版社, 2008:136-158. WANG X.Avionics countermeasure principle[M].Beijing:National Defense Industry Press, 2008:136-158(in Chinese).
[3]	张刚兵.单站无源定位与跟踪关键技术研究[D].南京: 南京航空航天大学, 2010. ZHANG G B.Research on key technology for single oserver passive location and tracking[D].Nanjin: Nanjing University of Aeronautics and Astronautics, 2010(in Chinese).
[4]	刘学.机载无源定位技术与跟踪算法研究[D].哈尔滨: 哈尔滨工程大学, 2011. LIU X.The research of technology and tracking algorithms for air-borne passive location[D].Harbin: Harbin Engineering University, 2011(in Chinese).
[5]	孙仲康, 郭福成, 冯道旺, 等.单站无源定位跟踪技术[M].北京:国防工业出版社, 2008:5-6. SUN Z K, GUO F C, FENG D W, et al.Passive location and tracking technology by single observer[M].Beijing:National Defense Industry Press, 2008:5-6(in Chinese).
[6]	许志伟, 王运锋, 张小琴.基于只测向的机载单站定位技术[J].四川大学学报(自然科学版), 2017, 54(2):293-297. https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX201702012.htm XU Z W, WANG Y F, ZHANG X Q.Airborne single-station passive location technology only based on bearing method[J].Journal of Sichuan University (Natural Science Edition), 2017, 54(2):293-297(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX201702012.htm
[7]	GERSHANOFF H.Experimental passive range and AOA system shows promise[J].Journal of Electronic Defence, 1992, 15(12):31-33.
[8]	ZHENG Q, CHEN J Q, YANG R J, et al.Research on technology based on orthogonal multi-station angle measurement method[J].Infrared Physics & Technology, 2017, 86:202-206. http://www.sciencedirect.com/science/article/pii/S1350449516307265
[9]	张金秀, 陶海红, 王渊.一种基于双基线旋转的改进干涉仪定位算法[J].北京理工大学学报, 2018, 38(3):320-324. https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG201803016.htm ZHANG J X, TAO H H, WANG Y.An improved locating algorithm based on double baselines rotating interferometer[J].Transactions of Beijing Institute of Technology, 2018, 38(3):320-324(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG201803016.htm
[10]	LI C, LIAO Y B.A DF method for the improved correlative interferometer[J].Journal of Xidian University, 2006, 33(3):400-403. http://www.researchgate.net/publication/291128879_A_DF_method_for_the_improved_correlative_interferometer
[11]	赵培焱, 彭华峰, 邓兵, 等.基于干涉相位的两步法高精度无模糊时延估计[J].系统工程与电子技术, 2018, 40(11):2410-2414. doi: 10.3969/j.issn.1001-506X.2018.11.03 ZHAO P Y, PENG H F, DENG B, et al.Two-stage high accuracy and unambiguous time delay estimation method based on interferometry phase[J].Systems Engineer and Electronics, 2018, 40(11):2410-2414(in Chinese). doi: 10.3969/j.issn.1001-506X.2018.11.03
[12]	侯建民.基于相位差变化率的空中运动单站对地面固定目标的无源定位[D].合肥: 合肥工业大学, 2015: 7-11. HOU J M.The phase difference rate of change-based passive location of ground fixed target by the air movement single observer[D].Hefei: Hefei University of Technology, 2015: 7-11(in Chinese).
[13]	WANG J H, WANG Y S, GUO T, et al.Rate of phase difference change estimation in single airborne passive locating system[J].Chinese Journal of Aeronautics, 2009, 22(2):184-190. doi: 10.1016/S1000-9361(08)60085-0
[14]	朱伟强, 黄培康, 马琴.基于相位差变化率测量的单站定位方法[J].系统工程与电子技术, 2008, 30(11):2108-2111. doi: 10.3321/j.issn:1001-506X.2008.11.018 ZHU W Q, HUANG P K, MA Q.Location method for phase difference rate of change with single observer[J].Systems Engineering and Electronics, 2008, 30(11):2108-2111(in Chinese). doi: 10.3321/j.issn:1001-506X.2008.11.018
[15]	SHAN Y H, AN W, SUN Z K.Passive location method based on phase rate of change[J].Chinese Journal of Aeronautics, 2002, 15(1):49-54. doi: 10.1016/S1000-9361(11)60130-1
[16]	郭福成, 贾兴江, 皇甫堪.仅用相位差变化率的机载单站无源定位方法及其误差分析[J].航空学报, 2009, 30(6):1090-1095. doi: 10.3321/j.issn:1000-6893.2009.06.020 GUO F C, JIA X J, HUANGFU K.A single observer passive localization method using phase difference changing rate only and its error analysis[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(6):1090-1095(in Chinese). doi: 10.3321/j.issn:1000-6893.2009.06.020
[17]	张敏, 郭福成, 周一宇, 等.运动单站干涉仪相位差直接定位方法[J].航空学报, 2013, 34(9):2185-2193. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201309021.htm ZHANG M, GUO F C, ZHOU Y Y, et al.A single moving observer direct position determination method using interferometer phase difference[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(9):2185-2193(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201309021.htm
[18]	张曼.基于高斯和的滤波算法研究[D].西安: 西安工程大学, 2015: 8-12. ZHANG M.Research on filtering algorithm based on Gauss sum[D].Xi'an: Xi'an Polytechnic University, 2015: 8-12(in Chinese).
[19]	LEONG P H, ARULAMPALAM S, LAMAHEWA T A, et al.A Gaussian-sum based cubature Kalman filter for bearings-only tracking[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2):1161-1176. doi: 10.1109/TAES.2013.6494405
[20]	曹亚琴, 秦宁宁, 杨乐.一种改进的双站时频差目标跟踪高斯和滤波算法[J].计算机与数字工程, 2018, 46(5):908-915. CAO Y Q, QING N N, YANG L.Enhanced Gaussian-sum filter for TDOA and FDOA-based tracking with two sensors[J].Computer & Digital Engineering, 2018, 46(5):908-915(in Chinese).
[21]	李曦, 杨乐, 郭福成, 等.高轨双星辐射源跟踪的高斯和-容积Kalman滤波算法[J].国防科技大学学报, 2016, 38(2):96-106. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201602017.htm LI X, YANG L, GUO F C, et al.Gaussian-sum based 5th-order cubature Kalman filter for source geolocation using dual GEO satellites[J].Journal of National University of Defense Technology, 2016, 38(2):96-106(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201602017.htm
[22]	BILIK I, TABRIKIAN J.MMSE-based filtering in presence of non-Gaussian system and measurement noise[J].IEEE Transactions on Aerospace and Electronic System, 2010, 46(3):1153-1170. doi: 10.1109/TAES.2010.5545180
[23]	王磊, 程向红, 李双喜.高斯和高阶无迹卡尔曼滤波算法[J].电子学报, 2017, 45(2):424-430. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU201702022.htm WANG L, CHENG X H, LI S X.Gaussian sum high order unscented Kalman filtering algorithm[J].Acta Electronica Sinica, 2017, 45(2):424-430(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU201702022.htm