空域扇区网络结构特性分析及韧性评估

王兴隆; 苗尚飞

doi:10.13700/j.bh.1001-5965.2020.0084

空域扇区网络结构特性分析及韧性评估

doi: 10.13700/j.bh.1001-5965.2020.0084

中国民航大学空中交通管理学院, 天津 300300

基金项目:

中央高校基本科研业务费专项资金 3122019191

详细信息

作者简介:
王兴隆男，硕士，副研究员。主要研究方向：空中交通流量管理、空域运行安全

苗尚飞男，硕士研究生。主要研究方向：空中交通流量管理、空域运行安全

通讯作者:
王兴隆, E-mail:xinglong1979@163.com

中图分类号: V11
计量
- 文章访问数: 793
- HTML全文浏览量: 158
- PDF下载量: 85
- 被引次数: 0
出版历程
- 收稿日期: 2020-03-05
- 录用日期: 2020-05-30
- 网络出版日期: 2021-05-20

Structural characteristics analysis and resilience assessment of airspace sector network

College of Air Traffic Management, Civil Aviation University of China, Tianjin 300300, China

Funds:

the Fundamental Research Funds for the Central Universities 3122019191

More Information

Corresponding author: WANG Xinglong, E-mail:xinglong1979@163.com

摘要

摘要:
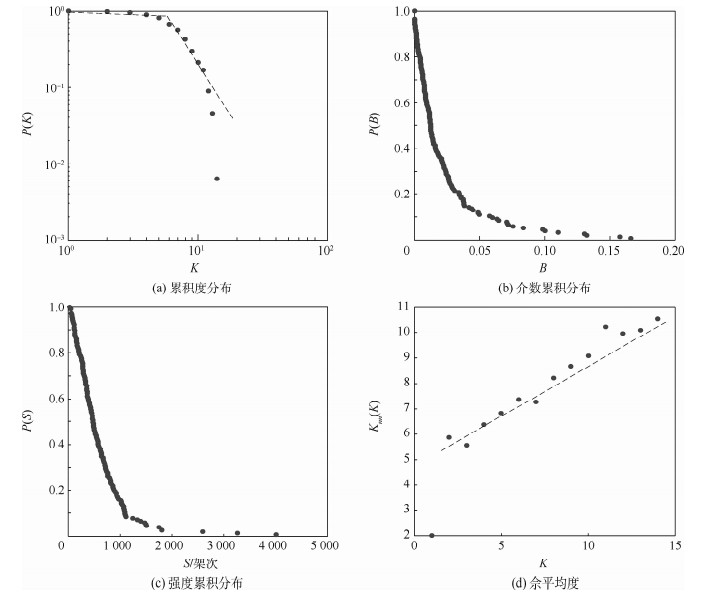
为保障扇区内航空器运行安全，提高扇区网络在外界干扰下的韧性，从而有效减轻航班延误和空域拥堵。首先，依据中国空域扇区划分规则，运用复杂网络理论构建中国空域扇区网络模型；然后，定义网络基本特征参数，对中国空域扇区网络结构特性进行分析，提出扇区网络韧性的概念，并采用一种定量评估方法对其进行度量；最后，对比分析不同恢复策略下的韧性指标，以此制定空域扇区网络在外界干扰下的最佳恢复策略，提高网络韧性。结果表明：中国空域扇区网络具有较大的平均最短路径长度和较小的聚类系数，度分布服从双段幂律分布，介数和强度服从指数分布。介数是影响空域扇区网络韧性最大的指标，采用介数恢复策略可显著提高外界干扰下空域扇区网络的韧性。
- 空域扇区 /
- 复杂网络 /
- 介数 /
- 网络效率 /
- 扇区网络韧性
Abstract:
In order to ensure the safety of aircraft operations in the sector, improve the resilience of the sector network under external disturbance, and thereby effectively reduce flight delays and airspace congestion, by using complex network theory, an airspace sector network model of China is established based on airspace sector division rules. Then, the structural characteristics of airspace sector network are analyzed by defining basic network parameters. In addition, the concept of sector network resilience is defined and a quantitative evaluation method is used to measure it. Finally, resilience indicators under different recovery strategies are comparatively analyzed, so as to develop the optimal recovery strategy of the sector network under external disturbance and improve the network resilience. The results show that the airspace sector network of China has a lengthy average shortest path and a small clustering coefficient. The degree distribution follows a double power-law distribution and the cumulative distributions of betweenness follow an exponential distribution. Among them, betweenness has the greatest impact on the resilience of airspacesector network. Adopting the betweenness recovery strategy can significantly improve the airspacesector network resilience under external disturbance.
- airspace sectors /
- complex network /
- betweenness /
- network efficiency /
- sector network resilience

HTML全文

图 1 特征参数分布

Figure 1. Distribution of characteristic parameters

下载: 全尺寸图片幻灯片

图 2 系统受损及韧性恢复过程

Figure 2. System damage and resilience recovery process

下载: 全尺寸图片幻灯片

图 3 随机扰动及不同恢复策略下的空域扇区网络效率

Figure 3. Airspace sector network efficiency under random disturbance and different recovery strategies

下载: 全尺寸图片幻灯片

图 4 度值扰动及不同恢复策略下的空域扇区网络效率

Figure 4. Airspace sector network efficiency under degree disturbance and different recovery strategies

下载: 全尺寸图片幻灯片

图 5 介数扰动及不同恢复策略下的空域扇区网络效率

Figure 5. Airspace sector network efficiency under betweenness disturbance and different recovery strategies

下载: 全尺寸图片幻灯片

图 6 综合韧性值

Figure 6. General resilience values

下载: 全尺寸图片幻灯片

表 1 空域扇区网络特征参数

Table 1. Airspace sector network characteristic parameters

特征参数	公式	含义
度		对于具有N个节点的空域扇区网络，节点i的度K_i表示空域扇区网络中与节点i存在航班联系的扇区的个数。e_ij表示若节点i与节点j相连，则e_ij=1，否则e_ij=0
累积度分布		表示度值不小于K的节点数所占的比例。P_k′为度分布，表示空域扇区网络中度为K的节点数占总节点数的比例
强度		表示经过扇区i的航班流量，V(i)表示扇区i的相邻扇区集合，ω_ij表示扇区i飞往扇区j的航班流量
聚类系数		表示节点i的K_i个邻节点间实际存在的边数与最大可能存在的边数之比，反应了扇区邻节点之间联系的紧密程度。E_i为扇区i相邻节点之间实际存在的边数
平均最短路径长度		表示空域扇区网络中连接任意两扇区之间最短距离的平均值，N为扇区节点个数，d_ij为扇区i和扇区j之间的最短距离
介数		节点i的介数表示空域扇区网络中所有最短路径中经过该扇区的数量比例，n_jk为扇区j和扇区k之间最短路径数，n_jk(i)为扇区j和扇区k之间最短路径中经过扇区i的数目
余平均度		K_i表示节点i的度，K_ij表示节点i的邻居节点的度。K_nni表示节点i的余平均度，K_nn(K)表示度为K的节点的余平均度
网络效率		E表示空域扇区网络的网络效率，若扇区i与扇区j之间没有路径连接时，d_ij=∞，网络效率E的取值范围为[0, 1]，E的值越大，网络连通性越好

下载: 导出CSV

参考文献(18)

[1]	曾小舟. 基于复杂网络理论的中国航空网络结构实证研究与分[D]. 南京: 南京航空航天大学, 2012: 15-30. ZENG X Z.Empirical research and analysis of Chinese aviation network structure based on complex network theory[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2012: 15-30(in Chinese).
[2]	CAI K Q, ZHANG J, DU W B, et al. Analysis of the Chinese air route network as a complex network[J]. Chinese Physics B, 2012, 21(2): 596-602.
[3]	ZANIN M, LILLO F. Modelling the air transport with complex networks: A short review[J]. The European Physical Journal Special Topics, 2013, 215(1): 5-21. doi: 10.1140/epjst/e2013-01711-9
[4]	武喜萍, 杨红雨, 韩松臣. 基于复杂网络的空中交通特征与延误传播分析[J]. 航空学报, 2017, 38(S1): 113-119. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB2017S1015.htm WU X P, YANG H Y, HAN S C. Analysis of properties and delay propagation of air traffic based on complex network[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(S1): 113-119(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB2017S1015.htm
[5]	傅超琦, 王瑛, 李超, 等. 不同增长机制下航空网络自愈特性[J]. 北京航空航天大学学报, 2018, 44(6): 1221-1229. doi: 10.13700/j.bh.1001-5965.2017.0485 FU C Q, WANG Y, LI C, et al. Research on self-healing characteristics of aviation network under different growth mechanisms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(6): 1221-1229(in Chinese). doi: 10.13700/j.bh.1001-5965.2017.0485
[6]	许欣华. 航空网络鲁棒性及延误传播相关性研究[D]. 南京: 南京航空航天大学, 2018: 9-21. XU X H.Research on robustness of air transportation network and flight delay correlation[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2018: 9-21(in Chinese).
[7]	REN G J, LU C Y, ZHU J, et al. Analyzing the topological characteristic and key nodes of Chinese air sector network[J]. International Journal of Modern Physics B, 2019, 33(11): 2-21. doi: 10.1142/S0217979219501005
[8]	HOSSEINI S, BARKER K, RAMIREZ-MARQUEZ J E. A review of definitions and measures of system resilience[J]. Reliability Engineering and System Safety, 2016, 145: 47-61. doi: 10.1016/j.ress.2015.08.006
[9]	NAN C, SANSAVINI G. A quantitative method for assessing resilience of interdependent infrastructures[J]. Reliability Engineering and System Safety, 2017, 157: 35-53. doi: 10.1016/j.ress.2016.08.013
[10]	崔琼, 李建华, 冉淏丹, 等. 基于任务能力的指挥信息系统超网络弹性度量[J]. 指挥与控制学报, 2017, 3(2): 137-143. doi: 10.3969/j.issn.2096-0204.2017.02.0137 CUI Q, LI J H, RAN H D, et al. Resilience measurement of command information system super-networkbased on mission capability[J]. Journal of Command and Control, 2017, 3(2): 137-143(in Chinese). doi: 10.3969/j.issn.2096-0204.2017.02.0137
[11]	崔琼, 李建华, 王宏, 等. 基于节点修复的网络化指挥信息系统弹性分析模型[J]. 计算机科学, 2018, 45(4): 117-121. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201804018.htm CUI Q, LI J H, WANG H, et al. Resilience analysis model of networked command information system based on node repairability[J]. Computer Science, 2018, 45(4): 117-121(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201804018.htm
[12]	TANG J Q, RUDOLF H H, MA X L. A resilience-oriented approach for quantitatively assessing recurrent spatial-temporal congestion on urban roads[J]. Plos One, 2018, 13(1): e0190616. doi: 10.1371/journal.pone.0190616
[13]	胡玉, 顾洁, 马睿, 等. 面向配电网弹性提升的智能软开关鲁棒优[J]. 电力自动化设备, 2019, 39(11): 85-91. https://www.cnki.com.cn/Article/CJFDTOTAL-DLZS201911014.htm HU Y, GU J, MA R, et al. SNOP robust optimization for distribution network resilience enhancement[J]. Electric Power Automation Equipment, 2019, 39(11): 85-91(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLZS201911014.htm
[14]	WANG Y J, ZHAN J M, XU X H, et al. Measuring the resilience of an airport network[J]. Chinese Journal of Aeronautics, 2019, 32(12): 2694-2705. doi: 10.1016/j.cja.2019.08.023
[15]	ADGER W N. Social and ecological resilience: Are they related [J]. Progress in Human Geography, 2000, 24(3): 347-364. doi: 10.1191/030913200701540465
[16]	ROSE A, LIAO S Y. Modeling regional economic resilience to disasters: A computable general equilibrium analysis of water service disruptions[J]. Social Science Electronic Publishing, 2005, 45(1): 75-122. http://www.tandfonline.com/servlet/linkout?suffix=CIT0027&dbid=16&doi=10.1080%2F09535314.2017.1369010&key=10.1111%2Fj.0022-4146.2005.00365.x
[17]	DINH L T T, PASMAN H, GAO X, et al. Resilience engineering of industrial processes: Principles and contributing factors[J]. Journal of Loss Prevention in the Process Industries, 2012, 25(2): 233-241. doi: 10.1016/j.jlp.2011.09.003
[18]	徐野. 复杂互联系统与网络鲁棒性研究[M]. 北京: 电子工业出版社, 2015: 37-40. XU Y. Study of robustness in complex interconnected system and networks[M]. Beijing: Publishing House of Electronics Industry, 2015: 37-40(in Chinese).