-
摘要:
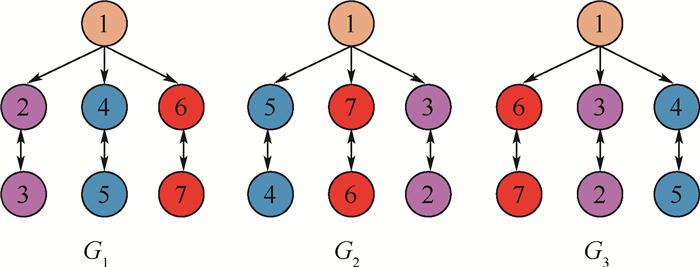
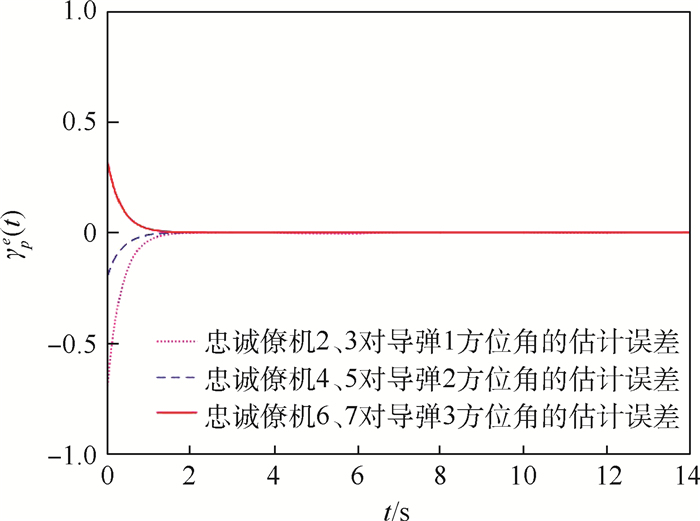
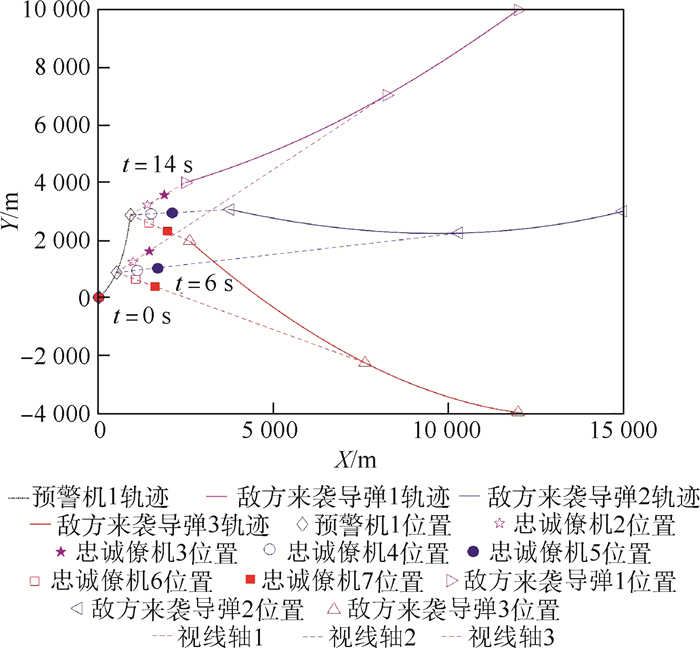
护航策略一直是各军事大国的重点研究内容之一,拒止环境具有强电磁干扰、强对抗博弈等特点,进而对护航策略提出了更高的要求。提出了一种基于分布式时变编队跟踪控制方法的护航策略,该策略中由高成本长机探测到敌方来袭导弹,在进行规避的同时,释放多个低成本僚机担任“忠诚僚机”。采用时变编队跟踪的控制方法,使僚机始终处于长机与敌方来袭导弹的视线轴上,必要时牺牲僚机以保全长机。针对敌方来袭导弹的方位角是全局信息,设计了分布式观测器对其进行估计。在拒止环境下,复杂电磁干扰带来通信时断时续,导致长机与僚机及僚机与僚机之间的通信拓扑存在切换。为应对电磁干扰对通信拓扑的破坏,提高抗电磁干扰能力,考虑僚机外部扰动和长机规避机动动作同时存在的情况,基于观测器理论、自适应控制理论和滑模控制理论,构造了具体通信拓扑切换机制的分布式控制协议,并利用Lyapunov理论证明了僚机采用该协议能够实现拒止环境下基于“忠诚僚机”的护航策略。通过仿真模拟导弹来袭场景,验证了所提策略的有效性。
Abstract:Escort strategy has always been one of the important studies of the major military powers and the denial environment with characteristics of strong electromagnetic interference and strong confrontation game puts forward higher requirements for escort strategy. This paper presents an escort strategy based on the distributed time-varying formation tracking control method. In this strategy, the high-cost lead aircraft detects the enemy missiles and releases several low-cost wingmen as loyal wingmen while moving for evasion. The time-varying formation tracking control methods are adopted to keep the wingmen on the line of sight axis associated with the lead aircraft and the enemy missiles, and then if necessary, the wingmen are sacrificed to protect the lead aircraft. As a result of the fact that the azimuth angles of enemy missiles are global information, the distributed observers are designed to estimate them. In the denial environment, the complex electromagnetic interference leads to the intermittent communication so that the communication topologies of systems composed by lead aircraft and wingmen are switched frequently. In order to deal with the damage of the communication topology caused by the electromagnetic interference and improve the ability of electromagnetic interference resistance, based on the observer theory, adaptive control theory and sliding mode control theory, a distributed control protocol with switching topologies is constructed under external disturbance of wingmen and the lead aircraft evasion. It is proven that the wingmen under the protocol can realize the escort strategy based on loyal wingman by Lyapunov theory in the denial environment. Finally, the effectiveness of the escort strategy is verified by simulating the attack scenario of the missiles.
-
Key words:
- escort strategy /
- denial environment /
- distributed observer /
- sliding mode control /
- adaptive control
-
[1] REN W.Consensus strategies for cooperative control of vehicle formations[J].IET Control Theory and Applications, 2007, 1(2):505-512. doi: 10.1049/iet-cta:20050401 [2] DONG X W, HU G Q.Time-varying formation control for general linear multi-agent systems with switching directed topologies[J].Automatica, 2016, 73:47-55. doi: 10.1016/j.automatica.2016.06.024 [3] HE Y L, ZHANG J Q, HOU Y Q, et al.Time-varying formation control for second-order discrete-time multi-agent systems with directed topologies and nonuniform communication delays[J].IEEE Access, 2019, 7:33517-33527. doi: 10.1109/ACCESS.2019.2904663 [4] WANG R, DONG X W, LI Q D, et al.Distributed adaptive formation control for linear swarm systems with time-varying formation and switching topologies[J].IEEE Access, 2016, 4:8995-9004. doi: 10.1109/ACCESS.2016.2646399 [5] HUA Y Z, DONG X W, LI Q D, et al.Robust adaptive time-varying formation control for high-order linear uncertain multi-agent systems[C]//201736th Chinese Control Conference (CCC), 2017: 8349-8354. [6] DONG X W, ZHOU Y, REN Z, et al.Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying[J].IEEE Transactions on Industrial Electronics, 2017, 64(6):5014-5024. doi: 10.1109/TIE.2016.2593656 [7] YU J L, DONG X W, LI Q D, et al.Practical time-varying formation tracking for multiple non-holonomic mobile robot systems based on the distributed extended state observers[J].IET Control Theory and Applications, 2018, 12(12):1737-1747. doi: 10.1049/iet-cta.2017.1397 [8] DONG X W, TAN Q K, LI Q D, et al.Necessary and sufficient conditions for average formation tracking of second-order multi-agent systems with multiple leaders[J].Journal of the Franklin Institute, 2017, 354(2):611-626. doi: 10.1016/j.jfranklin.2016.10.030 [9] YU J L, DONG X W, LI Q D, et al.Practical time-varying formation tracking for second-order nonlinear multiagent systems with multiple leaders using adaptive neural networks[J].IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(12):6015-6025. doi: 10.1109/TNNLS.2018.2817880 [10] SU H S, ZHANG J X, CHEN X.A stochastic sampling mechanism for time-varying formation of multiagent systems with multiple leaders and communication delays[J].IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(12):3699-3707. doi: 10.1109/TNNLS.2019.2891259 [11] HUA Y Z, DONG X W, WANG J B, at el.Time-varying output formation tracking for heterogeneous linear multi-agent systems with multiple leaders and switching topologies[J].Journal of the Franklin Institute, 2019, 356(1):539-560. doi: 10.1016/j.jfranklin.2018.11.006 [12] HUA Y Z, DONG X W, HU G Q, at el.Distributed time-varying output formation tracking for heterogeneous linear multi-agent systems with a nonautonomous leader of un-known input[J].IEEE Transactions on Automatic Control, 2019, 64(10):4292-4299. doi: 10.1109/TAC.2019.2893978 [13] HUA Y Z, DONG X W, HAN L, at el.Finite-time time-varying formation tracking for high-order multiagent systems with mismatched disturbances[J].IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2020, 50(10):3795-3803. [14] DUAN J, ZHANG H G, CAI Y L, at el.Finite-time time-varying output formation-tracking of heterogeneous linear multi-agent systems[J].Journal of the Franklin Institute, 2020, 357(2):926-941. doi: 10.1016/j.jfranklin.2019.10.012 [15] 田磊, 王蒙一, 赵启伦, 等.拓扑切换的集群系统分布式分组时变编队跟踪控制[J].中国科学:信息科学, 2020, 50(3):408-423.TIAN L, WANG M Y, ZHAO Q L, et al.Distributed time-varying group formation tracking for cluster systems with switching interaction topologies[J].Scientia Sinica Informations, 2020, 50(3):408-423(in Chinese). [16] WANG X J, WANG S P, YANG Z W, at el.Active fault-tolerant control strategy of large civil aircraft under elevator failures[J].Chinese Journal of Aeronautics, 2015, 28(6):1658-1666. doi: 10.1016/j.cja.2015.10.001 [17] REN W, BEARD R W.Consensus seeking in multiagent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control, 2005, 50(5):655-661. doi: 10.1109/TAC.2005.846556 [18] LI Z K, DUAN Z S, CHEN G R, at el.Consensus of multiagent systems and synchronization of complex networks:A unified viewpoint[J].IEEE Transactions on Circuits and Systems I:Regular Papers, 2010, 57(1):213-224. doi: 10.1109/TCSI.2009.2023937 -








 下载:
下载: