Comparative experimental study on wind tunnel based on WDPR-8 and machetes tail support
-
摘要:
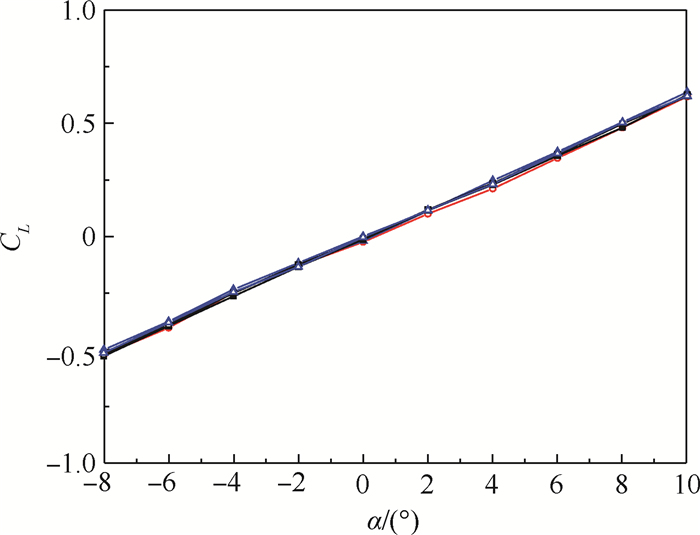
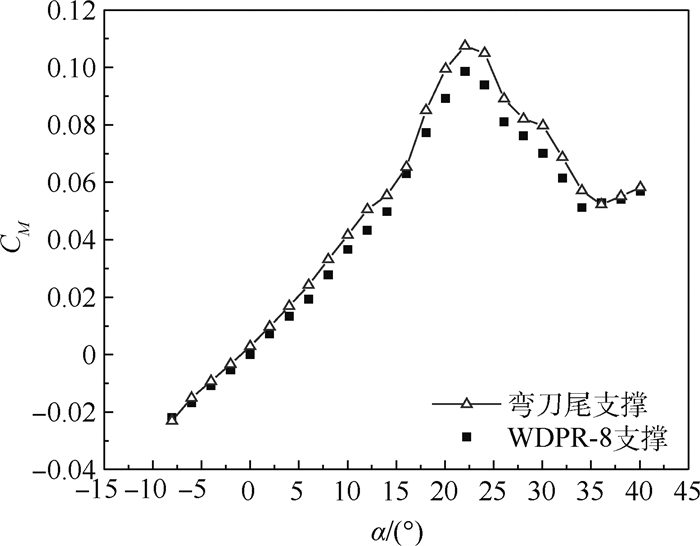
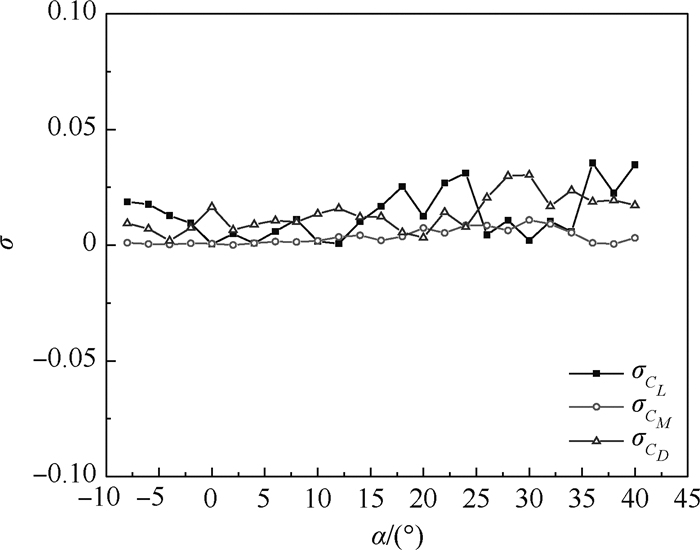
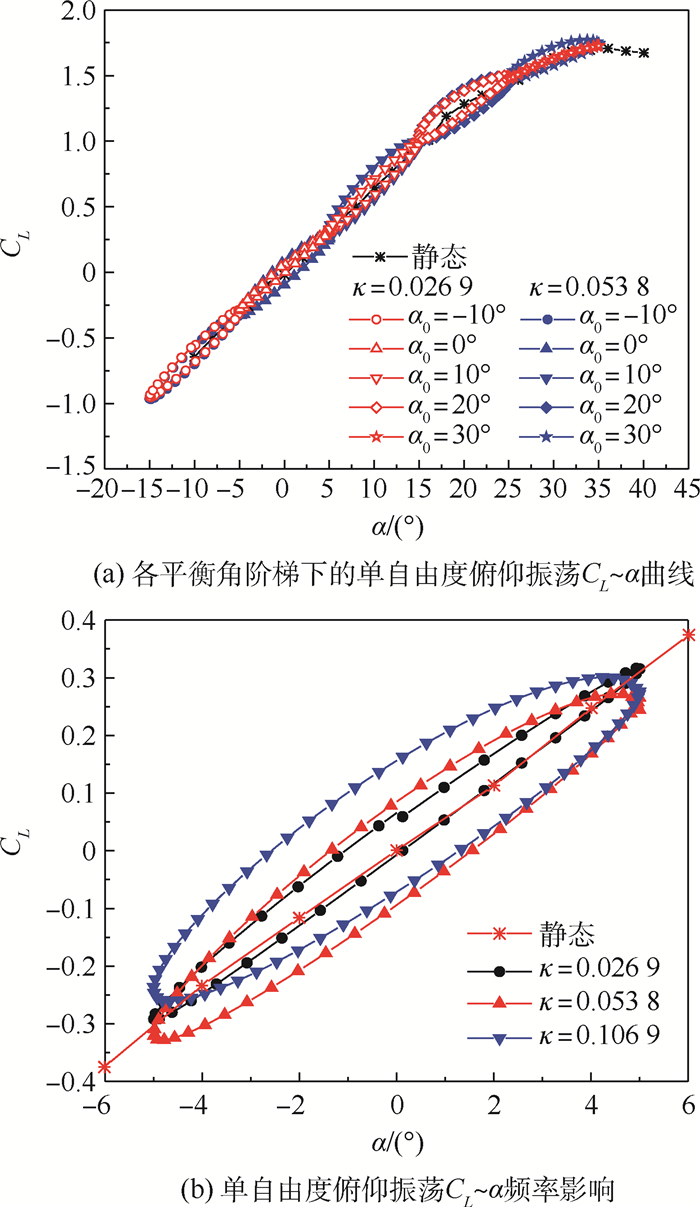
对国内近年设计的具有典型先进战斗机布局的动态试验标模，采用8绳牵引的绳牵引并联机器人（WDPR-8）支撑和传统弯刀尾支撑在FL-5风洞中进行对比吹风试验。根据风洞试验环境及仿真计算系统的刚度与工作空间，设计了满足要求的WDPR-8绳系结构和支撑机构，并建造了样机；在阻塞比及两心距足够小的前提下，保证了模型在两支撑系统中的通用性，以此设计内置六分量杆式天平的试验模型；利用绳拉力信号并联WDPR-8视觉采集系统与风洞VSS采集系统，实现气动力、机器视觉和绳拉力3个采集系统同步工作；在除支撑系统以外其他试验条件保持一致的条件下，进行重复性试验、纵向试验和横向试验。数据处理时，弯刀尾支撑进行了尾支架修正，WDPR-8支撑未修正。比较对照试验结果可得：两者在纵向试验的重复性试验所得升力系数最大均方差差别很小，2种支撑得到的升力系数、阻力系数和俯仰力矩系数的最大均方差不超过3.6%；横向试验在试验攻角范围内，2种支撑得到的侧向力系数对侧滑角的导数变化规律基本相同。用WDPR-8支撑进行的单自由度俯仰振荡试验得到的升力系数迟滞环曲线各环首尾连续，与静态升力系数曲线走势一致，且非定常迟滞环面积随减缩频率增大而增大，符合物理意义。试验研究结果反映出WDPR-8支撑的可行性及结果的有效性。
-
关键词:
- 风洞试验 /
- 对比试验 /
- 绳牵引并联机器人(WDPR) /
- 弯刀尾支撑 /
- 气动特性
Abstract:For a dynamic test model designed in China in recent years with a typical advanced fighter layout, Wire-Driven Parallel Robot with 8 Wires (WDPR-8) support and a traditional machetes tail support were used in a FL-5 wind tunnel for a comparative blow test. According to the wind tunnel test environment and the system's stiffness and working space, WDPR-8 wire structure and supporting mechanism were designed, and the prototype was built; for the blocking ratio and the distance between the two centers are small, the versatility of the model in the two support systems was ensured, and the test model of the built-in six-component bar balance was designed; the wire tension signal is used to parallel the WDPR-8 vision acquisition system and the wind tunnel VSS acquisition system to achieve that the three systems work synchronously. Repeatable tests, longitudinal tests, and transverse tests were performed under conditions in which the test conditions are consistent except for the support system. During data processing, the WDPR-8 was not modified for the tail bracket, and the tail support was modified for the tail bracket. The comparison of the test results of the two supports shows that the maximum mean square error of the lift coefficient obtained by the repeated tests in longitudinal test is near. The maximum mean square error of lift coefficient, drag coefficient, pitching moment coefficient obtained by the two supports do not exceed 3.6%. In the transverse test, the variation law of the derivative of the lateral force coefficient to the side slip angle obtained by the two supports are basically the same throughout the test angle of attack. The lift coefficient hysteresis loop curve obtained from the single-degree-of-freedom pitch oscillation test performed with WDPR-8 is consistent with the static lift coefficient curve. The lift coefficient hysteresis loop was continuous from beginning to end, and the area of the unsteady hysteresis loop increases with the shrinkage frequency, which is in line with the physical meaning. The experimental research results reflect the feasibility and effectiveness of the WDPR-8 support.
-
激光陀螺捷联惯导系统(Laser Strapdown Inertial Navigation System, LSINS)具有动态范围广、耐冲击振动、可靠性高等优点，远征一号、嫦娥探测器等空间飞行器及多数现役火箭均采用LSINS提供姿态、位置等导航信息。多表冗余惯导系统通过仪表冗余设计，显著提高系统的可靠性，国外如波音777飞机的FT/ADIRS (Fault-Tolerant/Air Data Inertial Reference System)容错大气数据参考系统和“德尔它”系列火箭的RIFCA (Redundant Inertial Flight Control Assembly)冗余激光捷联惯导系统[1]等都采用了多表冗余设计。国内对多表冗余惯导系统进行了多年的研究与探索，已有多型采用三正交加斜置冗余配置的惯导系统得到工程应用，其中斜置冗余仪表仅用于故障检测。
空间飞行器等起飞前需要通过初始对准获得姿态初值，目前普遍使用光学瞄准方案。与光学瞄准相比，惯导自对准需要的设备和人力更少，操作流程大大简化，更符合当前低成本、快速发射的发展趋势[2]。国内外的专家学者对晃动基座上的自对准技术进行了大量研究，提出了许多更优的自对准方案和自对准算法，显著提高了对准精度[3-6]。
对于多表冗余惯导系统而言，冗余仪表用于故障检测和隔离，同时还可通过数据融合技术提高惯导系统的测量和导航精度[7-10]。通过多传感器数据融合技术，充分利用所有的冗余测量数据，可以得到姿态和速度信息的最优估计值。数据融合技术可以有效抑制测量数据中的随机误差，为提高惯导系统自对准精度提供了另外一条有效途径。
本文基于某型多表冗余惯导系统，对数据融合技术在多表冗余惯导系统自对准中的应用及数据融合算法进行了研究。
1. 数据融合算法
1.1 惯导仪表构型
该型惯导系统采用三正交两斜置的十表(5只激光陀螺，5只石英加速度计)冗余设计，其中斜置仪表只用于判故。惯导系统中，陀螺和加速度计的安装定向方式如图 1所示，仪表测量矩阵如式(1)所示。
图 1 惯性仪表安装定向示意图Figure 1. Schematic diagram of inertial instrument installation orientation图 1中，X1Y1Z1为载体坐标系，OX1为纵轴，OY1为法向轴，OZ1为横向轴；XsYsZs为惯导坐标系，OS轴正向与OXs、OYs、OZs轴正向的夹角分别为125.9°、46.6°、115.4°，OT轴正向与OXs、OYs、OZs轴正向的夹角分别为46.5°、56.5°、118.0°；向量Gi和Ai分别为第i只陀螺和第i只加速度计的测量轴向，i=x, y, z, s, t。
(1) 1.2 基于最小二乘的数据融合算法
最小二乘估计(Least Square Estimation, LSE)的特点是算法简单，不必知道与被估计量及量测量有关的任何统计信息[11]。NASA的SIRU项目使用加权最小二乘(Weighted Least Squares Estimation, WLSE)算法进行冗余仪表的数据融合[12]。
对于测量系统：
(2) 式中：X为n维状态矢量；Z为m维量测量；H为m×n维量测矩阵，m＞n；V为m维测量噪声，其均值为零，方差阵为R。
X的最小二乘估计为
(3) 当多组测量数据精度并不完全相同时，可根据其精度质量通过加权的方法进行区别对待，能够有效提高估计精度。式(3)中，X的加权最小二乘估计为
(4) 式中：W为适当取值的正定加权矩阵。
如果取W=R－1，则称为马尔可夫估计，马尔可夫估计的均方误差比任何其他加权最小二乘估计的均方误差都要小[13]。
惯导系统测量方程可以简化表示为
(5) 式中：Ng和Na分别为陀螺和加速度计的测量输出，m维向量，m为陀螺或加速度计的数量；Kg和Ka分别为陀螺和加速度计的当量矩阵，m阶对角阵；Dg和Da分别为陀螺和加速度计零偏，m维向量；dt为系统采样时间间隔；Hg和Ha分别为陀螺和加速度计的一次项系数矩阵，也即测量矩阵，m×3维，当不考虑零部件加工和安装误差时，Hg=Ha；Δθ和ΔV分别为载体在dt时间内的角增量和速度增量，3维向量；Vg和Va分别为陀螺和加速度计的测量噪声，m维向量，均值为零，其方差阵分别为Rg和Ra。
Δθ和ΔV的加权最小二乘估计为
(6) 式中:Wg和Wa分别为陀螺和加速度计输出的加权矩阵。
Δθ和ΔV的马尔可夫估计为
(7) 1.3 算法精度分析
不考虑零部件加工和安装误差，陀螺和加速度计系统的测量矩阵均如式(1)所示，假设5只仪表(陀螺或者加速度计)的测量精度相同，输出标准差均为1σ。
1) 只使用正交仪表数据
3个轴向的输出标准差为
3个轴合成输出的标准差为
2) 同时使用5只仪表数据
根据式(3)所示的融合算法，可以计算出3个轴向的输出标准差分别为
3个轴合成输出的标准差为
由上可以看出，相较于只使用3个正交轴向仪表数据，通过数据融合同时使用5只仪表数据，可以有效降低惯导系统各个轴向及3个轴合成输出的噪声水平，3个轴合成标准差由
2. Monte Carlo仿真
编写了MATLAB仿真计算程序，对静基座上的自对准进行仿真，仿真中惯导坐标系与地理坐标系(东北天坐标系)重合。工程上通常挑选精度较好的仪表安装在正交轴向，斜置方向仪表精度略差，如正交仪表精度为0.01 (°)/h左右，而斜置仪表精度范围为0.015~0.02(°)/h。因此，仿真中假设斜置仪表噪声标准差比正交仪表高50%，并使用马尔可夫估计进行数据融合。为对算法在不同仪表精度下的融合效果进行对比，共进行了4组不同精度的仿真，每组进行500次Monte Carlo打靶。分别通过：①只使用3只正交仪表数据直接解算；②通过式(7)进行5只仪表的数据融合，2种方法得到的自对准结果进行对比，偏航角的统计结果如表 1所示。
表 1 偏航角误差的Monte Carlo仿真结果对比Table 1. Comparison of Monte Carlo simulation results of yaw angle error序号 噪声标准差 三表解算 五表数据融合 比值 均值/(10-5(°)) 方差/(10-4(°)) 均值/(10-5(°)) 方差/(10-4(°)) 均值 方差 1组 σg=0.03 σa=0.001 1.21 0.095 1.12 0.079 0.93 0.83 2组 σg=0.06 σa=0.002 2.39 0.18 1.83 0.15 0.77 0.83 3组 σg=0.09 σa=0.003 3.47 0.27 3.30 0.24 0.95 0.89 4组 σg=0.12 σa=0.004 4.79 0.36 4.37 0.32 0.91 0.89 均值 0.89 0.86 结果表明，相较于只使用正交仪表数据，通过数据融合同时使用5只仪表数据，可以有效提高惯导偏航角自对准精度，其中误差均值降低了11%，对准结果统计标准差降低了14%。这表明对于如式(1)所示的三正交两斜置惯导系统，即便斜置仪表精度显著低于正交仪表，通过数据融合，仍然能够显著提高惯导的自对准精度，使斜置冗余仪表数据得到充分利用。
3. 自对准试验和算法改进
3.1 静态自对准试验
为验证本文中数据融合算法的有效性，利用该型惯导系统在大理石平板上进行了静态自对准试验。5只激光陀螺的零偏稳定性在0.01 (°)/h左右。试验时，将惯组固联在六面体工装上，惯导按照地理坐标系(东北天坐标系)放置，工装靠紧大理石平板靠块，如图 2所示，对准时间5 min，共进行12组试验。
考虑试验现场条件无法获取惯导系统真实的航向基准，为了评估算法的有效性，采用在同一方位下进行多次对准，以多次对准结果的标准差的方法间接进行评估[14]。每组试验数据分别通过3只正交仪表直接解算和5只仪表数据融合2种方法进行处理，得到Δθ和ΔV，然后进行自对准。
试验中使用如式(7)所示的马尔可夫估计进行数据融合，对2种方法的自对准结果进行对比，如表 2所示。只使用正交仪表直接解算时，偏航角的统计标准差为2.8′(1σ)，同时使用5只仪表数据进行数据融合时，偏航角的统计标准差为2.4′(1σ)，精度提高了14%。
表 2 偏航角自对准结果对比Table 2. Self-alignment result comparison of yaw angles序号 偏航角/(′) 三表解算 五表数据融合 1 -7.5 -4.4 2 1.5 0.9 3 -3.9 -5.8 4 -2.1 -3.9 5 -5.7 -3.7 6 -7.5 -5.8 7 -0.3 -0.3 8 -0.3 -1.4 9 -0.2 -2.1 10 -2.1 0.1 11 -2.1 -3.6 12 -3.9 1.0 标准差 2.8 2.4 3.2 加权矩阵的优化
该型惯导系统各仪表原始输出均为脉冲形式，间隔20 ms，输出脉冲数对应惯导在惯性坐标系下的角增量和速度增量。静态自对准试验时，由于地球自转角速度和重力加速度较小，导致仪表输出的量化误差明显。试验中仪表的一段输出数据如表 3所示，其中Ai和Gi(i=x, y, z, s, t)分别为第i只陀螺和加速度计的脉冲输出。同时，仪表输出噪声非白噪声形式，尤其是激光陀螺。因此，对仪表输出直接取方差不能反映仪表精度状况，影响了基于数据方差的马尔可夫估计的数据融合算法的效果。
表 3 仪表 20 ms脉冲增量输出Table 3. Incremental pulse output of sensors with 20 ms interval序号 Ax Ay Az As At Gx Gy Gz Gs Gt 1 0 0 49 -21 -23 0 0 0 0 0 2 0 -1 48 -21 -23 0 0 0 0 0 3 0 0 49 -21 -23 0 0 0 0 0 4 0 0 49 -20 -23 0 0 0 0 0 5 0 0 48 -21 -23 0 0 0 0 0 6 0 0 48 -21 -24 0 1 1 0 0 7 0 0 49 -21 -22 0 0 0 0 0 8 0 0 49 -21 -23 0 0 0 0 0 9 0 0 48 -21 -23 0 0 0 0 0 10 0 0 49 -21 -23 0 0 0 0 1 惯性仪表的零偏稳定性是衡量仪表精度、影响导航误差的重要参数，同时仪表零偏稳定性也比较容易准确获得。因此，选择各仪表的零偏稳定性作为加权系数，构造如式(8)所示的加权矩阵，其中Ωi(i=x, y, z, s, t)为第i只陀螺和加速度计的零偏稳定性。
(8) 使用如式(8)所示的加权矩阵和加权最小二乘估计的数据融合算法, 对试验数据重新进行处理，结果如表 4所示，偏航角的统计标准差为2.1′(1σ)。相较于马尔可夫估计，通过加权最小二乘算法和式(8)所示的加权矩阵进行数据融合，自对准精度进一步提高。
表 4 五表数据融合的偏航角自对准结果Table 4. Self-alignment results of yaw angles by data fusion of five instruments序号 偏航角/(′) 1 -4.3 2 1.0 3 -4.6 4 -3.0 5 -3.4 6 -5.1 7 -0.1 8 -0.9 9 -1.5 10 -0.2 11 -2.7 12 0.2 标准差 2.1 多表冗余惯导系统在实际工程应用中需要先经故障诊断技术对故障仪表进行诊断隔离，再使用正常仪表完成系统重构。惯导系统自对准过程中，火箭受发射场阵风等干扰因素的影响，箭体产生顺风向和横风向晃动[15]，但晃动频率较低、量级较小；同时可以通过地测对载荷和火箭惯导系统的输出进行地面判读。因此，初始对准过程中不用担心惯导系统冗余仪表的判故问题，上述数据融合算法有一定的工程实用价值。
4. 结论
基于某型三正交两斜置冗余的十表惯导系统，针对其自对准过程中的数据融合问题：
1) 通过分析和仿真，证明数据融合技术可以有效提高多表冗余惯导系统的自对准精度。
2) 开展惯导静态自对准试验，结果表明，相较于只使用正交仪表的数据，数据融合可以使斜置冗余仪表的数据得到充分利用，系统自对准精度提高了16%。
3) 在静态自对准试验的基础上，构造了基于仪表零偏稳定性的加权矩阵，改进后的算法比马尔可夫估计的略有提高。
-
图 3 WDPR-8支撑原理样机结构示意图
Figure 3. Schematic diagram of structure of WDPR-8 support prototype
图 5 WDPR-8支撑机构运动学关系示意图
Figure 5. Schematic diagram of WDPR-8 support institutional kinematics relationship
图 7 应用于弯刀尾支撑下的模型结构剖面图
Figure 7. Model structure profile applied to mathetes tail support
图 9 基于WDPR-8支撑试验结果精度验证
Figure 9. Accuracy verification based on WDPR-8 support test results
图 10 升力特性曲线对比(V0=30 m/s)
Figure 10. Comparison of lift characteristic curves atV0=30 m/s
图 12 俯仰力矩系数曲线对比(V0=30 m/s)
Figure 12. Comparison of pitching moment coefficient curves at V0=30 m/s
图 13 两种支撑结果气动系数的均方根误差曲线(V0=30 m/s)
Figure 13. Mean square error curves of aerodynamic coefficients of two kinds of support results at V0=30 m/s
图 14 纵向静稳定度对比(V0=30 m/s)
Figure 14. Comparison of longitudinal static stabilityat V0=30 m/s
图 16 单自由度俯仰振荡升力系数曲线
Figure 16. Single-degree-of-freedom pitching oscillation lift coefficient curves
表 1 WDPR-8支撑的结构参数
Table 1. Table 1 Structure parameter of WDPR-8 support
i Pi/mm Bi/mm xb yb zb xg yg zg 1 -332 125 -4 240 733 -1 910 2 -332 -125 -4 240 -733 -1 910 3 0 -642 -13 -443 -599 -1 910 4 0 642 -13 -443 599 -1 910 5 0 61 14 -347 346 -70 6 -332 125 4 77 588 -70 7 -332 -125 4 77 -588 -70 8 0 -61 14 -347 -346 -70 
下载: 导出CSV
表 2 风洞试验工况
Table 2. State and condition of wind tunnel test
参数 数值 风速V0/(m·s-1) 20, 30 攻角/(°) -8~40 侧滑角/(°) 0, -5, -10, -15 室温/℃ 15 模型 动态试验标模
下载: 导出CSV
表 3 重复性试验的均方差结果
Table 3. Mean variance results of repeatability tests
α/(°) 均方差/% WDPR-8支撑 弯刀尾支撑 -8 1.048 0.685 -6 1.125 0.742 -4 0.972 0.798 -2 0.741 0.674 0 1.077 0.847 2 1.072 0.831 4 1.350 0.917 6 1.116 0.771 8 1.050 0.760 10 1.070 1.156
下载: 导出CSV
表 4 两种支撑所得侧向力系数的最大均方根误差
Table 4. Maximum mean square error of lateral force coefficient obtained from two supports
α/(°) σCYmax/% β=0° β=-5° β=-10° β=-15° -8~10 0.521 0.655 0.828 1.396 -8~12 0.786 0.788 0.828 1.396 -8~40 5.286 3.755 5.353 10.627
下载: 导出CSV
-
[1] TUTTLE M H.Support interference of wind tunnel models: A selective annotated bibliography[R].Washington, D.C.: NASA Langley Research Center, 1981. [2] 李周复.风洞试验手册[M].北京:航空工业出版社, 2015:140.LI Z F.Wind tunnel test manual[M].Beijing:Aviation Industry Press, 2015:140(in Chinese). [3] 王勋年, 孙正荣.低速风洞试验[M].北京:国防工业出版社, 2002:326.WANG X N, SUN Z R.Low speed wind tunnel test[M].Beijing:National Defense Industry Press, 2002:326(in Chinese). [4] XIAO Y W, LIN Q, ZHENG Y Q, et al.Model aerodynamic tests with a wire-driven parallel suspension system in low-speed wind tunnel[J].Chinese Journal of Aeronautics, 2010, 23(4):393-400. doi: 10.1016/S1000-9361(09)60233-8 [5] 王晓光, 林麒.风洞试验绳牵引并联支撑技术研究进展[J].航空学报, 2018, 39(10):122064.WANG X G, LIN Q.Progress in wire-driven parallel suspension technologies in wind tunnel tests[J].Acta Aeronautica et Astronautica Sinica, 2018, 39(10):122064(in Chinese). [6] LAMBERT T J, VUKASINOVIC B, GLEZER A.A six degrees of freedom dynamic wire-driven traverse[J].Aerospace, 2016, 3(2):11. doi: 10.3390/aerospace3020011 [7] LAMBERT T J, VUKASINOVIC B, GLEZER A.Aerodynamic flow control of wake dynamics coupled to a moving bluff body: AIAA 2016-4081[R].Reston: AIAA, 2016. [8] STURM C, LALO W, BRUCKMANN T.Wire robot suspension systems for wind tunnels[J].Wind Tunnels and Experimental Fluid Dynamics Research, 2011, 7(27):709. [9] LAFOURCASE P, LLIBRE M, REBOULET C.Design of a parallel wire-driven manipulator for wind tunnels[C]//Proceedings of the Workshop on Fundamental Issues and Future Research Directions for Parallel Mechanisms and Manipulators, 2002: 187-194. [10] LAFOURCASE P, LLIBRE M, REBOULET C.First steps toward a sketch-based design methodology for wire-driven manipulators[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Piscataway: IEEE Press, 2003: 143-148. [11] LAFOURCASE P.Study of parallel manipulators with cables, design of an active suspension for wind tunnel[D].Paris: ENSAE, 2004: 22-29. [12] GRIFFIN S A, CROOKS R S, MOLE P J.Vane support system (VSS)-A new generation wind tunnel model support system: AIAA-91-0398[R].Reston: AIAA, 1991. [13] 冀洋锋, 林麒, 胡正红, 等.基于绳系并联机器人支撑系统的SDM动导数试验可行性研究[J].航空学报, 2017, 38(11):121330.JI Y F, LIN Q, HU Z H, et al.Research on feasibility of dynamic stability derivatives test of SDM with wire-driven parallel robot suspension system[J].Acta Aeronautica et Astronautica Sinica, 2017, 38(11):121330(in Chinese). [14] 林麒, 冀洋锋.一种可实现风洞虚拟飞行的模型绳索支撑系统: CN104132795A[P].2014-11-05.LIN Q, JI Y F.Model rope support system capable of realizing virtual flight of wind tunnel: CN104132795A[P].2014-11-05(in Chinese). [15] 国防科学技术工业委员会.高速风洞和低速风洞测力实验精度指标: GJB 1061-91[S].北京: 国防科学技术工业委员会, 1991.National Defense Science, Technology and Industry Commission.Requirement for force-Test precision of high and low speed wind tunnels: GJB 1061-91[S].Beijing: National Defense Science, Technology and Industry Commission, 1991(in Chinese). [16] 郝卫东, 司永昌, 高静.民机低速风洞测力试验技术研究[J].流体力学实验与测量, 2004, 18(4):34-37. doi: 10.3969/j.issn.1672-9897.2004.04.008HAO W D, SI Y C, GAO J.Investigation of civil airplane force measurement in low speed wind tunnel[J].Fluid Mechanics Experiment and Measurement, 2004, 18(4):34-37(in Chinese). doi: 10.3969/j.issn.1672-9897.2004.04.008 [17] 王勋年, 祝明红, 孙传宝.低速大迎角尾撑支架干扰试验研究[J].实验流体力学, 2007, 21(2):8-12. doi: 10.3969/j.issn.1672-9897.2007.02.002WANG X N, ZHU M H, SUN C B.Investigation on the interference of rear sting supports at high angle of attack in low speed wind-tunnel[J].Journal of Experiments in Fluid Mechanics, 2007, 21(2):8-12(in Chinese). doi: 10.3969/j.issn.1672-9897.2007.02.002 [18] 殷春平, 陈艺峰, 吴了泥, 等.基于粒子群算法的摄像机标定过程优化[J].机电工程, 2012, 29(1):100-103.YIN C P, CHEN Y F, WU L N, et al.Optimization of camera calibration process based on PSO algorithm[J].Mechanical & Electrical Engineering Magazine, 2012, 29(1):100-103(in Chinese). [19] 陈艺峰.悬挂式飞行器模型姿态的单目视觉测量方法研究[D].厦门: 厦门大学, 2012: 74.CHEN Y F.Research on monocular vision measurement method for model attitude of suspended aircraft[D].Xiamen: Xiamen University, 2012: 74(in Chinese). [20] 赵小见, 赵磊, 冯峰, 等.某空腔低速流动噪声风洞试验[J].航空学报, 2015, 36(7):2145-2154.ZHAO X J, ZHAO L, FENG F, et al.Wind tunnel test into noise induced by low-speed cavity flow[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(7):2145-2154(in Chinese). [21] 李国帅, 魏志, 李巍, 等.现代试验设计方法在高速风洞试验中的应用[J].航空学报, 2015, 36(3):782-788.LI G S, WEI Z, LI W, et al.Using modern design of experiments methodologies for high speed wind tunnel tests[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(3):782-788(in Chinese). [22] 刘大伟, 熊贵天, 刘洋, 等.宽体客机高速风洞试验数据修正方法[J].航空学报, 2019, 40(2):522205.LIU D W, XIONG G T, LIU Y, et al.Method of test data correction for wide-body aircraft in high speed wind tunnel[J].Acta Aeronautica et Astronautica Sinica, 2019, 40(2):522205(in Chinese). -
下载:
下载:
点击查看大图
计量
- 文章访问数: 677
- HTML全文浏览量: 128
- PDF下载量: 231
- 被引次数: 0
