高超声速伸缩式变形飞行器再入制导方法

岳彩红; 唐胜景; 王肖; 郭杰

doi:10.13700/j.bh.1001-5965.2020.0183

高超声速伸缩式变形飞行器再入制导方法

doi: 10.13700/j.bh.1001-5965.2020.0183

岳彩红¹,
唐胜景^1, ,,
王肖^{1, 2},
郭杰¹

1.
北京理工大学宇航学院, 北京 100081
2.
中国运载火箭技术研究院战术武器事业部, 北京 100076

基金项目:

国家自然科学基金 11572036

详细信息

通讯作者:
唐胜景, E-mail: tangsj@bit.edu.cn

中图分类号: V221⁺.3;TB553
计量
- 文章访问数: 649
- HTML全文浏览量: 220
- PDF下载量: 126
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-14
- 录用日期: 2020-06-19
- 网络出版日期: 2021-06-20

Reentry guidance method of hypersonic telescopic deformable vehicle

YUE Caihong¹,
TANG Shengjing^{1
, ,},
WANG Xiao^{1, 2},
GUO Jie¹

1.
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
2.
Tactical Weapons Division, China Academy of Launch Vehicle Technology, Beijing 100076, China

Funds:

National Natural Science Foundation of China 11572036

More Information

Corresponding author: TANG Shengjing, E-mail: tangsj@bit.edu.cn

摘要

摘要:
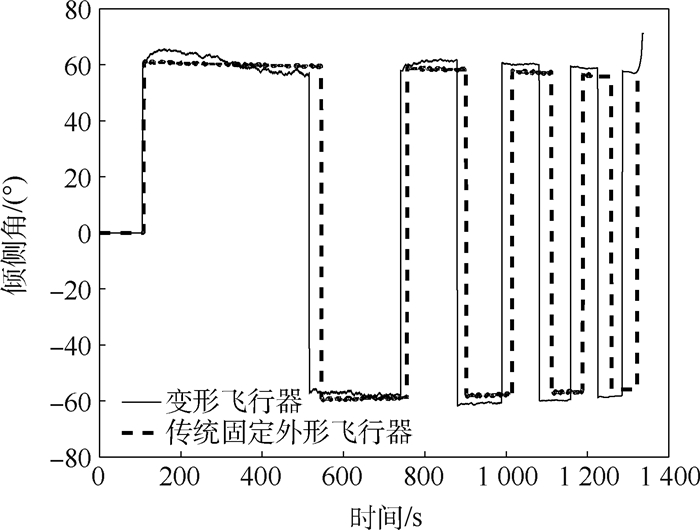
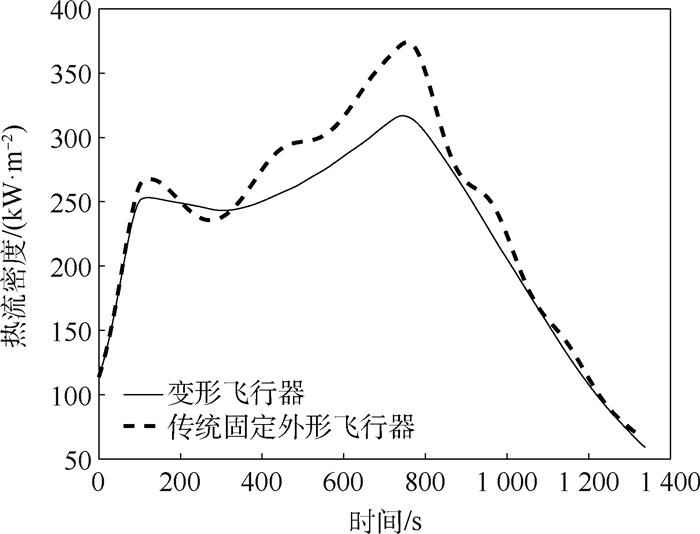
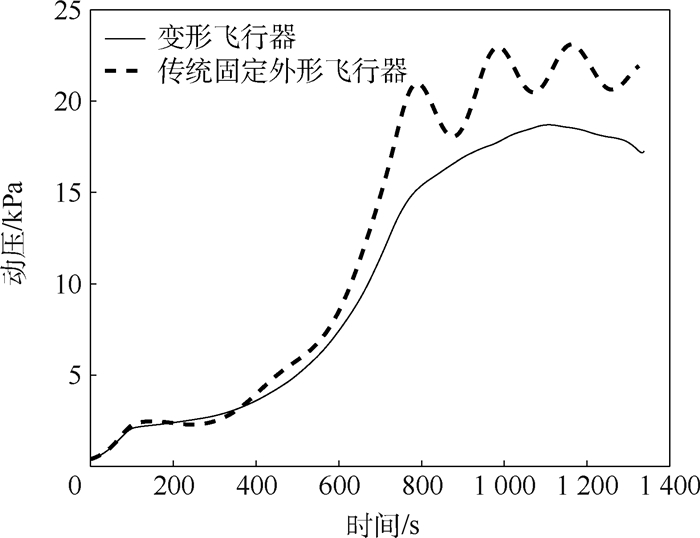
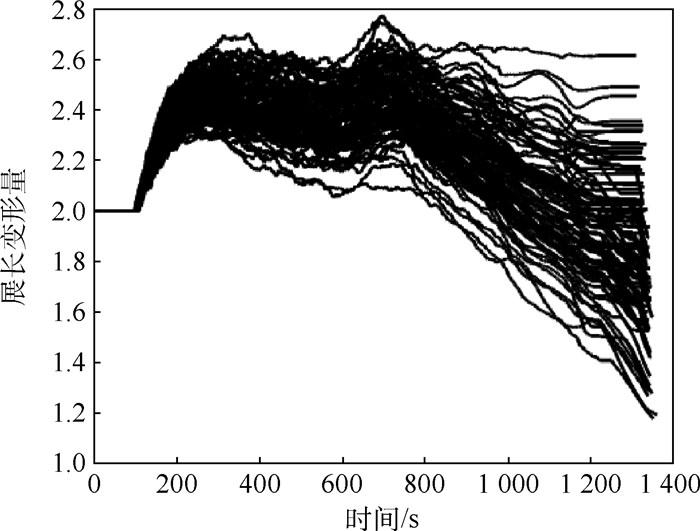
针对高超声速变形飞行器再入制导问题，提出了一种采用伸缩式机翼的高超声速变形飞行器外形方案，建立了含有展长变形量的气动模型和动力学模型。将该变形飞行器的展长变形量扩展为控制变量，分析了倾侧角、展长变形量和终端航程、高度之间的关系。在此基础上，利用倾侧角和展长变形量在线预测剩余航程和终端高度，通过数值方法校正2个控制量以满足航程约束和高度约束，通过航向角走廊确定倾侧角符号。仿真结果表明：该变形飞行器再入制导方法制导精度高，相比于传统固定外形飞行器终端约束能力更强、轨迹更加平滑，且在扰动条件下具有一定鲁棒性。
- 变形飞行器 /
- 高超声速飞行器 /
- 再入制导 /
- 预测校正 /
- 制导能力分析
Abstract:
Aimed at the reentry guidance problem for hypersonic deformable vehicle, firstly, a shaping plan of hypersonic deformable vehicle using telescopic wings is proposed, and the aerodynamic model and dynamic model with elongation deformation are established. Secondly, with the elongation deformation being extended to control variables, the relationships between bank angle, elongation deformation and terminal range, altitude are analyzed. On this basis, the remaining range and terminal altitude are predicted by bank angle and elongation deformation, the two control variables are corrected by numerical algorithm to meet the range and altitude constraints, and the bank angle symbol is determined through the heading angle corridor. Simulated results show that the reentry guidance method of the deformable vehicle has high guidance accuracy, having stronger terminal restraint ability and smoother trajectory compared with the fixedshape vehicle, and it has certain robustness under disturbance conditions.
- deformable vehicle /
- hypersonic vehicle /
- reentry guidance /
- predictor-corrector /
- guidance performance analysis

HTML全文

图 1 传统固定外形飞行器构型

Figure 1. Configuration of traditional fixed shape vehicle

下载: 全尺寸图片幻灯片

图 2 高超声速伸缩式变形飞行器平面示意图

Figure 2. Schematic diagram of hypersonic telescopic deformable vehicle

下载: 全尺寸图片幻灯片

图 3 变形2升力系数曲线

Figure 3. Lift coefficient curves of morphing 2

下载: 全尺寸图片幻灯片

图 4 变形2阻力系数曲线

Figure 4. Drag coefficient curves of morphing 2

下载: 全尺寸图片幻灯片

图 5 变形2升阻比曲线

Figure 5. Lift to drag ratio curves of morphing 2

下载: 全尺寸图片幻灯片

图 6 不同外形升力系数随攻角变化曲线

Figure 6. Variation of lift coefficient with attack anglein different shapes

下载: 全尺寸图片幻灯片

图 7 不同外形阻力系数随攻角变化曲线

Figure 7. Variation of drag coefficient with attack anglein different shapes

下载: 全尺寸图片幻灯片

图 8 不同外形升阻比随攻角变化曲线

Figure 8. Variation of lift to drag ratio with attack angle in different shapes

下载: 全尺寸图片幻灯片

图 9 终端航程与倾侧角和展长变形量的关系

Figure 9. Relationship among range, bank angle and deformation

下载: 全尺寸图片幻灯片

图 10 终端高度与倾侧角和展长变形量的关系

Figure 10. Relationship among height, bank angle and deformation

下载: 全尺寸图片幻灯片

图 11 标准条件下的高度-速度曲线

Figure 11. Altitude-velocity curves under standard condition

下载: 全尺寸图片幻灯片

图 12 标准条件下的地面轨迹

Figure 12. Ground tracks under standard condition

下载: 全尺寸图片幻灯片

图 13 标准条件下的倾侧角曲线

Figure 13. Bank angles under standard condition

下载: 全尺寸图片幻灯片

图 14 标准条件下的展长变形量曲线

Figure 14. Deformation under standard condition

下载: 全尺寸图片幻灯片

图 15 标准条件下的热流密度曲线

Figure 15. Heating flux under standard condition

下载: 全尺寸图片幻灯片

图 16 标准条件下的动压曲线

Figure 16. Dynamic pressures under standard condition

下载: 全尺寸图片幻灯片

图 17 标准条件下的过载曲线

Figure 17. Overloads under standard condition

下载: 全尺寸图片幻灯片

图 18 扰动条件下的高度-速度曲线

Figure 18. Altitude-velocity curves under parameter perturbation

下载: 全尺寸图片幻灯片

图 19 扰动条件下的地面轨迹

Figure 19. Ground tracks under parameter perturbation

下载: 全尺寸图片幻灯片

图 20 扰动条件下的高度-速度终端误差分布

Figure 20. Altitude-velocity terminal error distribution

下载: 全尺寸图片幻灯片

图 21 扰动条件下的经度-纬度终端误差分布

Figure 21. Longitude-latitude terminal error distribution

下载: 全尺寸图片幻灯片

图 22 扰动条件下的热流密度曲线

Figure 22. Heating flux under parameter perturbation

下载: 全尺寸图片幻灯片

图 23 扰动条件下的动压曲线

Figure 23. Dynamic pressures under parameter perturbation

下载: 全尺寸图片幻灯片

图 24 扰动条件下的过载曲线

Figure 24. Overloads under parameter perturbation

下载: 全尺寸图片幻灯片

图 25 扰动条件下的展长变形量曲线

Figure 25. Deformations under parameter perturbation

下载: 全尺寸图片幻灯片

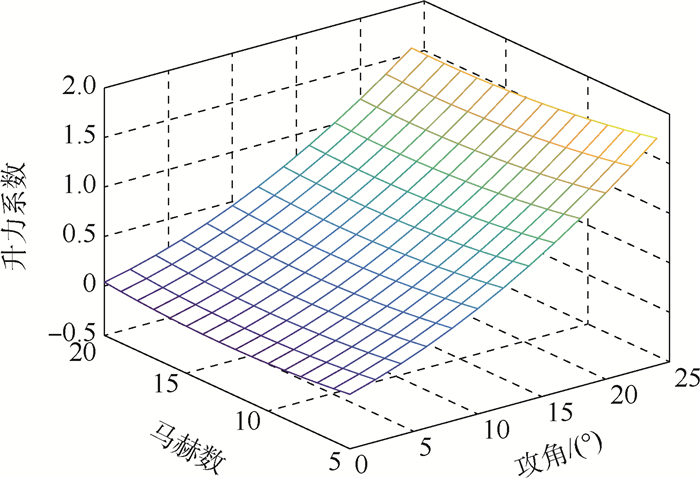
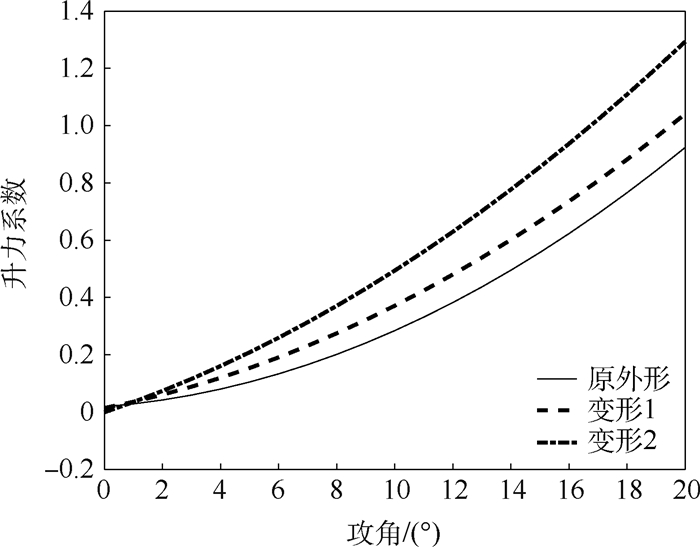
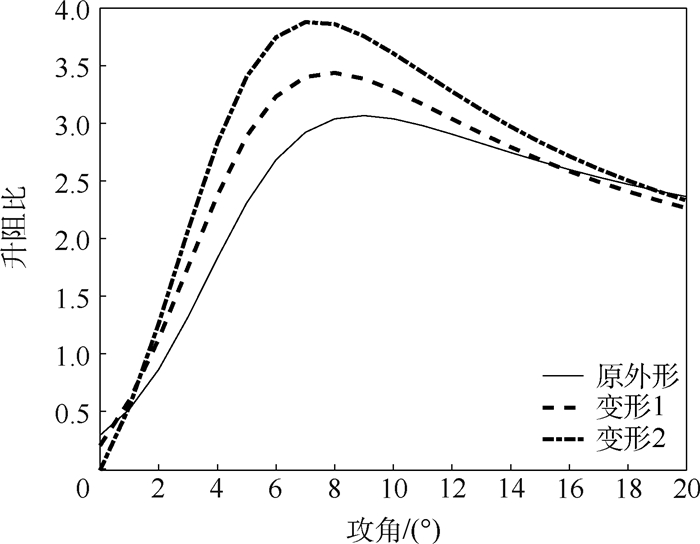
表 1 升力系数拟合结果

Table 1. Lift coefficient fitting results

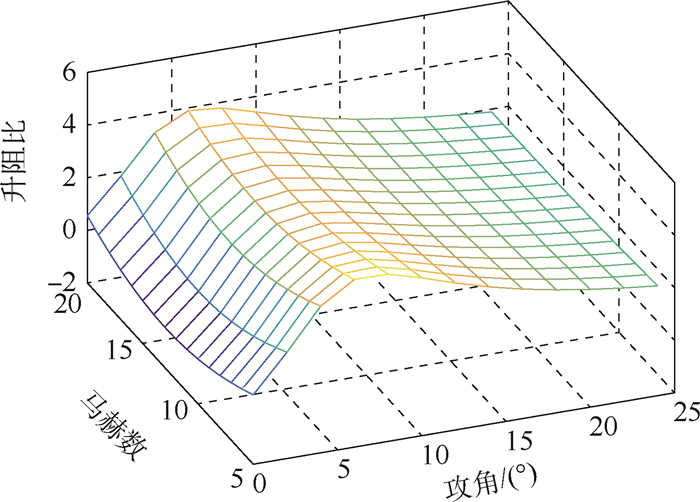
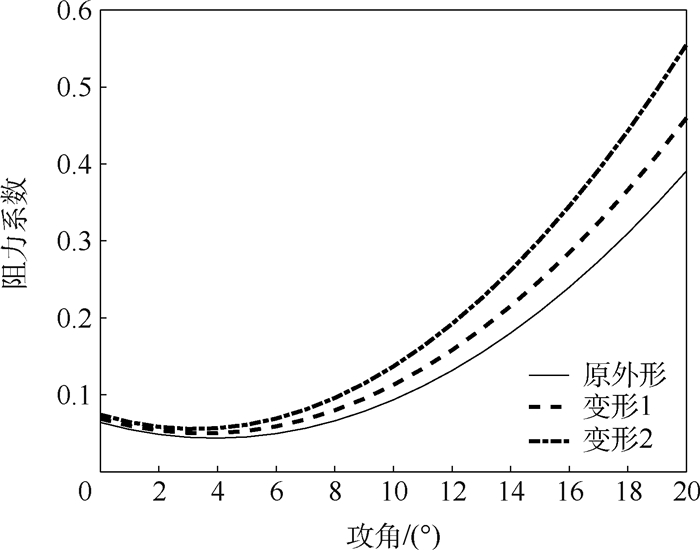
外形	m₀	m₁	m₂	m₃	m₄	m₅	RS系数
原外形	0.121 0	-0.017 4	0.403 2	0.000 58	0.005 9	6.137	0.988 9
变形1	0.213 5	-0.035 6	1.250 0	0.001 33	-0.012 2	5.128	0.990 9
变形2	0.190 3	-0.034 7	2.243 0	0.001 35	-0.035 0	4.998	0.985 2

下载: 导出CSV

表 2 阻力系数拟合结果

Table 2. Drag coefficient fitting results

外形	n₀	n₁	n₂	n₃	n₄	n₅	RS系数
原外形	0.037 72	0.005 36	-0.679 1	-0.000 3	0.009 98	4.398	0.944 6
变形1	0.065 33	0.001 05	-0.642 1	-0.000 2	0.003 22	4.972	0.986 3
变形2	0.090 67	-0.002 60	-0.674 7	-0.000 1	0.001 92	5.834	0.993 2

下载: 导出CSV

表 3 再入任务初始状态

Table 3. Initial states of reentry task

参数	H₀/km	λ₀/(°)	ϕ₀/(°)	V₀/(m·s^-1)	θ₀/(°)	ψ₀/(°)
数值	80	10	-20	7 100	-1	45

下载: 导出CSV

表 4 再入任务终端状态

Table 4. Terminal states of reentry task

参数	H_f/km	λ_f/(°)	ϕ_f/(°)	V_f/(m·s^-1)
数值	35	57	15	2 000

下载: 导出CSV

表 5 终端误差

Table 5. Terminal errors

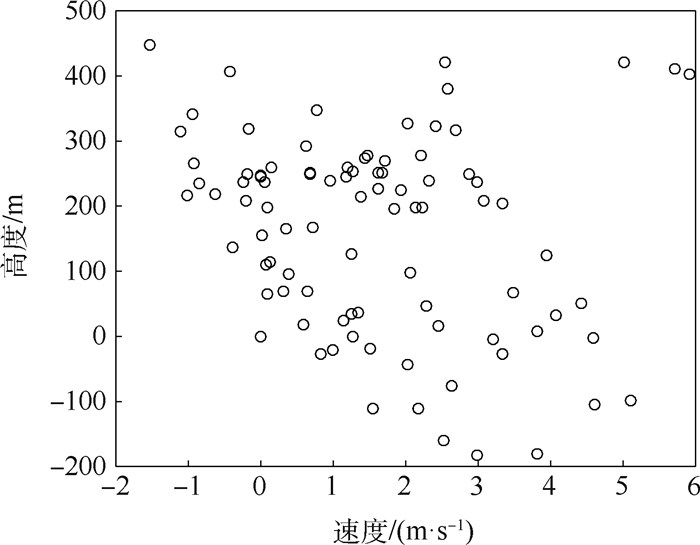
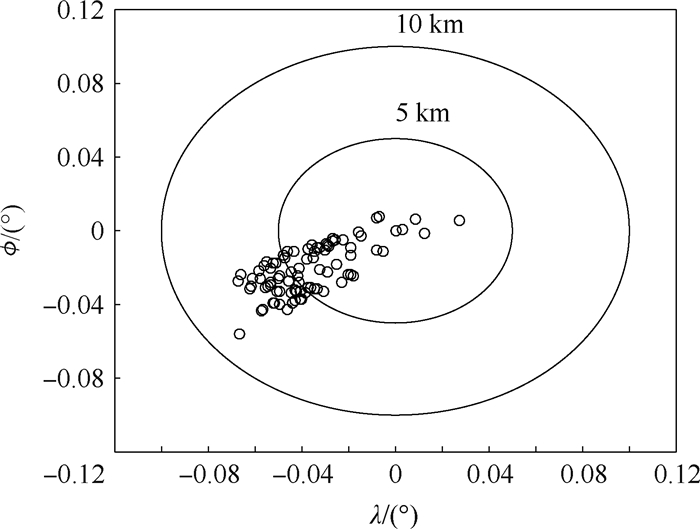
对象	Δ H_f/m	Δ V_f/(m·s^-1)	Δ s_f/m
变形飞行器	190.1	-3.4	3 884.4
传统固定外形飞行器	-1 426.6	6.6	4 558.8
变形飞行器	190.1	-3.4	3 884.4
传统固定外形飞行器	-1 426.6	6.6	4 558.8

下载: 导出CSV

表 6 扰动参数

Table 6. Disturbance parameters

参数	H₀/km	λ₀/(°)	ϕ₀/(°)	V₀/(m·s^-1)	θ₀/(°)	ψ₀/(°)	m/%	ρ/%	C_L/%	C_D/%
3 σ	1	0.5	0.5	30	0.1	0.5	5	10	5	5

下载: 导出CSV

参考文献(18)

[1]	李广华, 张洪波, 汤国建. 高超声速滑翔飞行器典型弹道特性分析[J]. 宇航学报, 2015, 36(4): 397-403. doi: 10.3873/j.issn.1000-1328.2015.04.005 LI G H, ZHANG H B, TANG G J. Typical trajectory characteristics of hypersonic glide vehicle[J]. Journal of Astronautics, 2015, 36(4): 397-403(in Chinese). doi: 10.3873/j.issn.1000-1328.2015.04.005
[2]	穆凌霞, 王新民, 谢蓉, 等. 高超音速飞行器及其制导控制技术综述[J]. 哈尔滨工业大学学报, 2019, 51(3): 1-14. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX201903001.htm MU L X, WANG X M, XIE R, et al. A survey of the hypersonic flight vehicle and its guidance and control technology[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 1-14(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX201903001.htm
[3]	张灿, 林旭斌, 胡冬冬, 等. 2018年国外高超声速飞行器技术发展综述[J]. 飞航导弹, 2019(2): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-FHDD201902001.htm ZHANG C, LIN X B, HU D D, et al. A survey of foreign hypersonic vehicle technology development in 2018[J]. Aerodynamic Missile Journal, 2019(2): 1-5(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHDD201902001.htm
[4]	张远龙, 谢愈. 滑翔飞行器弹道规划与制导方法综述[J]. 航空学报, 2020, 41(1): 50-62. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202001003.htm ZHANG Y L, XIE Y. Review of trajectory planning and guidance methods for gliding vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(1): 50-62(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202001003.htm
[5]	BARBARINO S, BILGEN O, AJAJ R M, et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(9): 823-877. doi: 10.1177/1045389X11414084
[6]	VALASEK J, DOEBBLER J, TANDALE M D, et al. Improved adaptive-reinforcement learning control for morphing unmanned air vehicles[J]. IEEE Transactions on Systems, Man, and Cybernetics. Part B: Cybernetics, 2008, 38(4): 1014-1020. doi: 10.1109/TSMCB.2008.922018
[7]	郭建国, 吴林旭, 周军. 非对称变翼飞行器复合控制系统设计[J]. 宇航学报, 2018, 39(1): 52-59. https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201801008.htm GUO J G, WU L X, ZHOU J. Compound control system design for asymmetric morphing-wing aircraft[J]. Journal of Astronautics, 2018, 39(1): 52-59(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201801008.htm
[8]	WICKENHEISER A, GARCIA E. Perching aerodynamics and trajectory optimization[C]//Active and Passive Smart Structures and Integrated System 2007. Bellingham: SPIE, 2007, 6525: 1-9.
[9]	MIR I, MAQSOOD A, EISA S A, et al. Optimal morphing-augmented dynamic soaring maneuvers for unmanned air vehicle capable of span and sweep morphologies[J]. Aerospace Science and Technology, 2018, 79: 17-36. doi: 10.1016/j.ast.2018.05.024
[10]	彭悟宇, 杨涛, 涂建秋, 等. 高超声速变形飞行器翼面变形模式分析[J]. 国防科技大学学报, 2018, 40(3): 15-21. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201803003.htm PENG W Y, YANG T, TU J Q, et al. Analysis on wing deformation modes of hypersonic morphing aircraft[J]. Journal of National University of Defense Technology, 2018, 40(3): 15-21(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201803003.htm
[11]	彭悟宇, 杨涛, 王常悦, 等. 高超声速伸缩翼变形飞行器轨迹多目标优化[J]. 国防科技大学学报, 2019, 41(1): 41-47. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201901007.htm PENG W Y, YANG T, WANG C Y, et al. Trajectory multi-objective optimization for hypersonic telescopic wing morphing aircraft[J]. Journal of National University of Defense Technology, 2019, 41(1): 41-47(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201901007.htm
[12]	陈铁彪, 龚旻, 王洪波, 等. 临近空间可变形滑翔飞行器轨迹优化与性能分析[J]. 宇航学报, 2018, 39(9): 944-952. https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201809001.htm CHEN T B, GONG M, WANG H B, et al. Trajectory optimization and performance analysis of the near-space morphing glide vehicles[J]. Journal of Astronautics, 2018, 39(9): 944-952(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201809001.htm
[13]	BAO C Y, WANG P, TANG G J. Integrated guidance and control for hypersonic morphing missile based on variable span auxiliary control[J]. International Journal of Aerospace Engineering, 2019, 2019: 1-20. http://www.researchgate.net/publication/332883498_Integrated_Guidance_and_Control_for_Hypersonic_Morphing_Missile_Based_on_Variable_Span_Auxiliary_Control
[14]	储培, 倪昆, 程林, 等. 基于反步滑模的高超声速变体飞行器鲁棒控制[J]. 计算机仿真, 2018, 35(8): 41-45. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201808010.htm CHU P, NI K, CHENG L, et al. Robust control of hypersonic morphing vehicle based on backstepping sliding mode control[J]. Computer Simulation, 2018, 35(8): 41-45(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201808010.htm
[15]	SHEN Z J, LU P. Onboard generation of three-dimensional constrained entry trajectories[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111-121. doi: 10.2514/2.5021
[16]	王肖, 唐胜景, 祁帅, 等. 带终端高度约束的再入预测校正制导[J]. 战术导弹技术, 2018(4): 70-77. https://www.cnki.com.cn/Article/CJFDTOTAL-ZSDD201804012.htm WANG X, TANG S J, QI S, et al. Predictor-corrector entry guidance with terminal altitude constraint[J]. Tactical Missile Technology, 2018(4): 70-77(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZSDD201804012.htm
[17]	徐瑞民. 二元非线性方程组求根的牛顿迭代法[J]. 山东轻工业学院学报(自然科学版), 2009, 23(4): 89-91. https://www.cnki.com.cn/Article/CJFDTOTAL-SQGX200904026.htm XU R M. Newton's method for the nonlinear function of two independent variables[J]. Journal of Shandong Institute of Light Industry(Natural Science Edition), 2009, 23(4): 89-91(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SQGX200904026.htm
[18]	XUE S B, LU P. Constrained predictor-corrector entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273-1281. http://smartsearch.nstl.gov.cn/paper_detail.html?id=448d328b892994fee5bcdec542cee157