弹性欧拉梁大变形分析的椭圆积分统一形式

安朝; 谢长川; 杨超

doi:10.13700/j.bh.1001-5965.2020.0186

弹性欧拉梁大变形分析的椭圆积分统一形式

doi: 10.13700/j.bh.1001-5965.2020.0186

北京航空航天大学航空科学与工程学院, 北京 100083

详细信息

通讯作者:
谢长川. E-mail: xiechangc@buaa.edu.cn

中图分类号: O341
计量
- 文章访问数: 746
- HTML全文浏览量: 187
- PDF下载量: 259
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-14
- 录用日期: 2020-06-30
- 网络出版日期: 2021-07-20

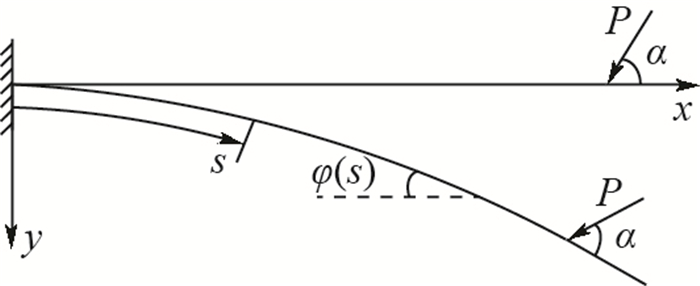
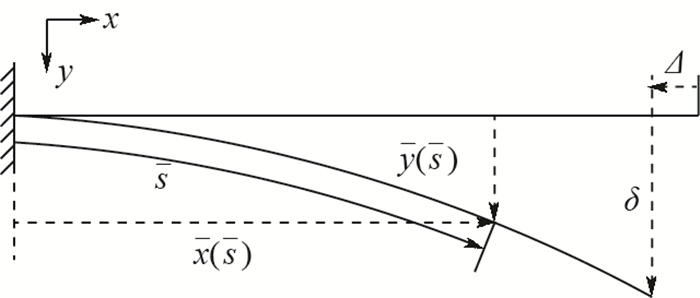
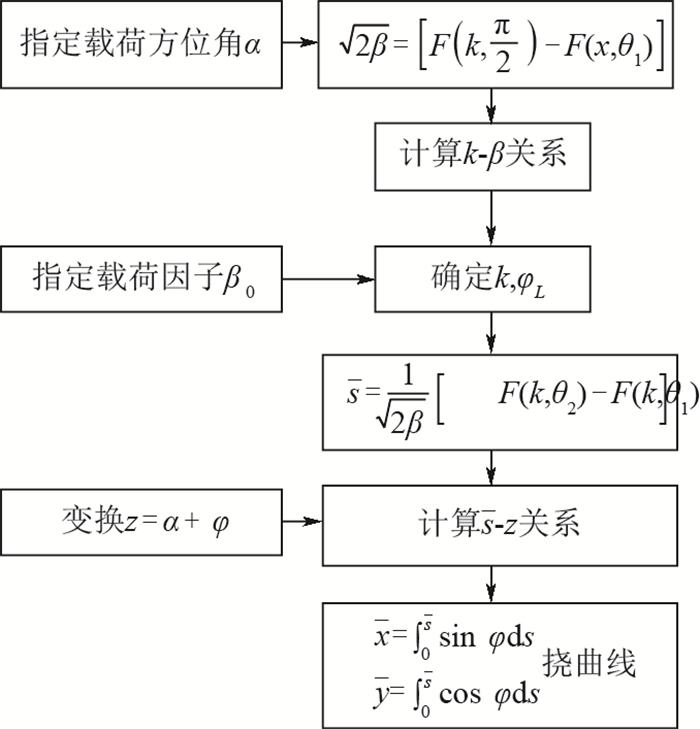
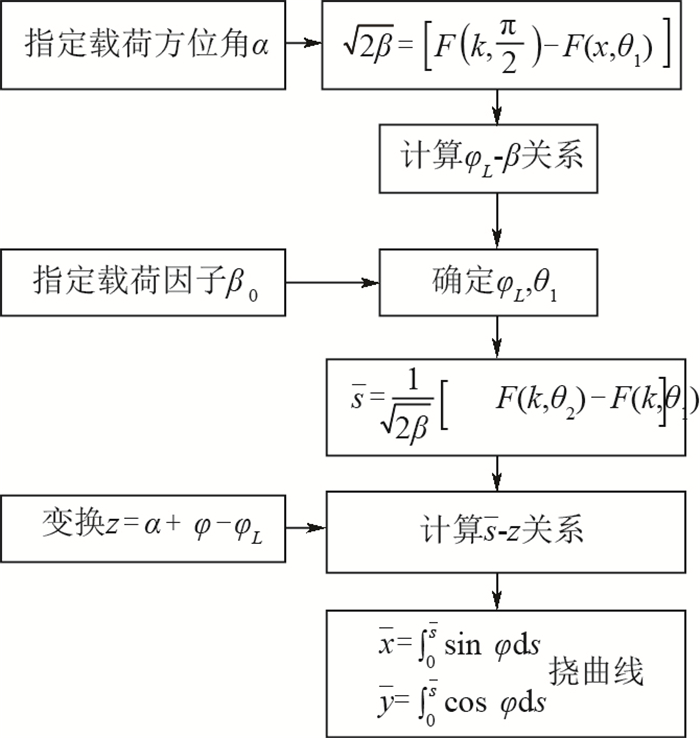
Unified form of large deflection analysis of elastic Euler beam based on elliptic integral

School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China

More Information

Corresponding author: XIE Changchuan. E-mail: xiechangc@buaa.edu.cn

摘要

摘要:
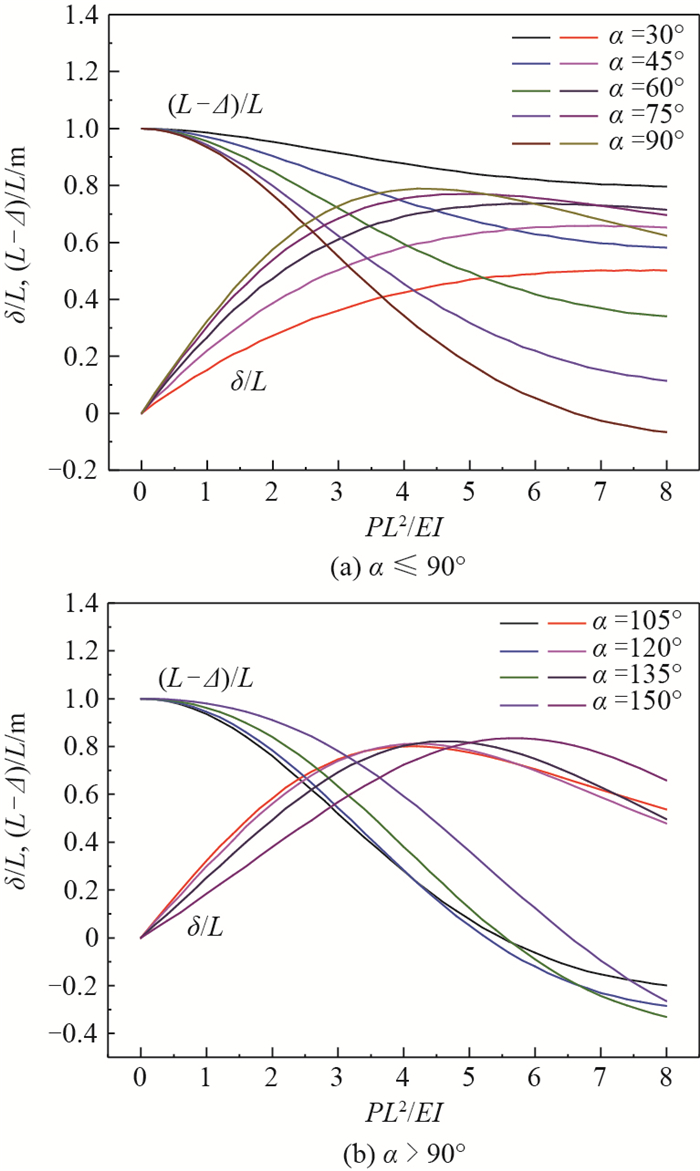
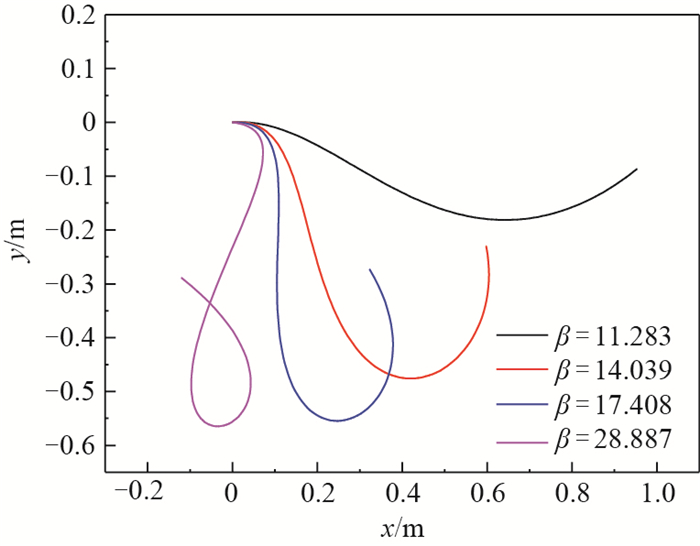
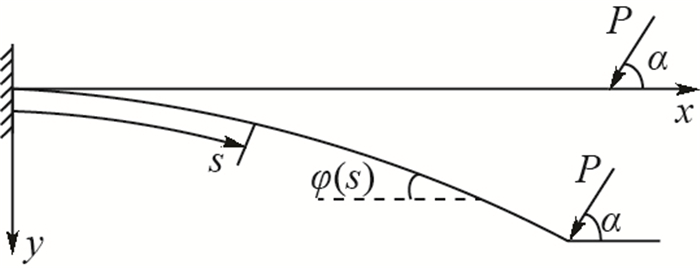
一端固支、一端受集中载荷的欧拉梁受载问题是一种基础的力学模型，具有重要的理论研究意义。针对传统的线性求解方法在大变形分析中不适用及无法计算中心定向受压杆在载荷系数超过临界值后屈曲变形的问题，提出一种非线性精确解来进行受集中载荷梁的大变形计算方法。通过椭圆积分形式来推导受集中载荷梁的变形表达，考虑在固支梁自由端加载任意角度下的定向载荷及随动载荷，给出形式统一的梁大变形方程，求解一定载荷因子系数及载荷方位角组合下的变形结果；同时利用此形式对定向受压杆的平衡分支解问题进行了分析。所提方法计算结果准确，可以应用于弹性欧拉梁受定向及随动载荷的大变形分析。
- 大变形梁 /
- 椭圆积分 /
- 随动载荷 /
- 平衡分支解 /
- 压杆稳定性
Abstract:
The loading problem of Euler beam with one end clamped and one end having concentrated load is a basic mechanical model, which has important theoretical significance. In order to solve the problem that the traditional linear method is not applicable to large deflection analysis and cannot calculate the post buckling deflection of the central direction compressed column when the load coefficient exceeds the critical value, a nonlinear exact solution is proposed to calculate the large deformation of the beam under concentrated load. In this paper, the elliptic integral form is used to derive the deflection expression of the beam under concentrated load. Considering the dead force and follower force at any angle on the free end of the fixed-supported beam, a large deflection equation of the beam in a unified form is given. The deflection results under the combination of load factor and load angle are calculated. At the same time, the balance branch solution of the compressed column with dead force is analyzed using this form. The calculation results of this method are accurate and can be applied to the large deflection analysis of elastic beam under dead force and follower force.
- large deflection beam /
- elliptic integral /
- follower force /
- balance branch solution /
- stability of compressed column

HTML全文

图 1 定向载荷作用下梁几何关系

Figure 1. Geometric relationship of beam with dead force

下载: 全尺寸图片幻灯片

图 2 随动载荷作用下梁几何关系

Figure 2. Geometric relationship of beam with follower force

下载: 全尺寸图片幻灯片

图 3 梁变形挠曲线

Figure 3. Deflection curves of beam

下载: 全尺寸图片幻灯片

图 4 梁端部受定向载荷计算流程

Figure 4. Flowchart of calculation with dead force at the end of beam

下载: 全尺寸图片幻灯片

图 5 梁端部受随动载荷计算流程

Figure 5. Flowchart of calculation with follower force at the end of beam

下载: 全尺寸图片幻灯片

图 6 梁端部受定向载荷挠曲线

Figure 6. Deflection curves with dead force at the end of beam

下载: 全尺寸图片幻灯片

图 7 梁端部受随动载荷挠曲线

Figure 7. Deflection curves with follower force at the end of beam

下载: 全尺寸图片幻灯片

图 8 定向载荷下梁变形对比(α=90°)

Figure 8. Contrast of beam deflection with dead force (α=90°)

下载: 全尺寸图片幻灯片

图 9 定向载荷下梁变形

Figure 9. Deflection of beam with dead force

下载: 全尺寸图片幻灯片

图 10 随动载荷下梁变形

Figure 10. Deflection of beam with follower force

下载: 全尺寸图片幻灯片

图 11 平衡Ⅰ态解曲线

Figure 11. Solution curves of balance branchⅠ

下载: 全尺寸图片幻灯片

图 12 平衡Ⅱ态解曲线

Figure 12. Solution curves of balance branch Ⅱ

下载: 全尺寸图片幻灯片

图 13 平衡Ⅲ态解曲线

Figure 13. Solution curves of balance branch Ⅲ

下载: 全尺寸图片幻灯片

表 1 梁模型参数

Table 1. Parameters of beam model

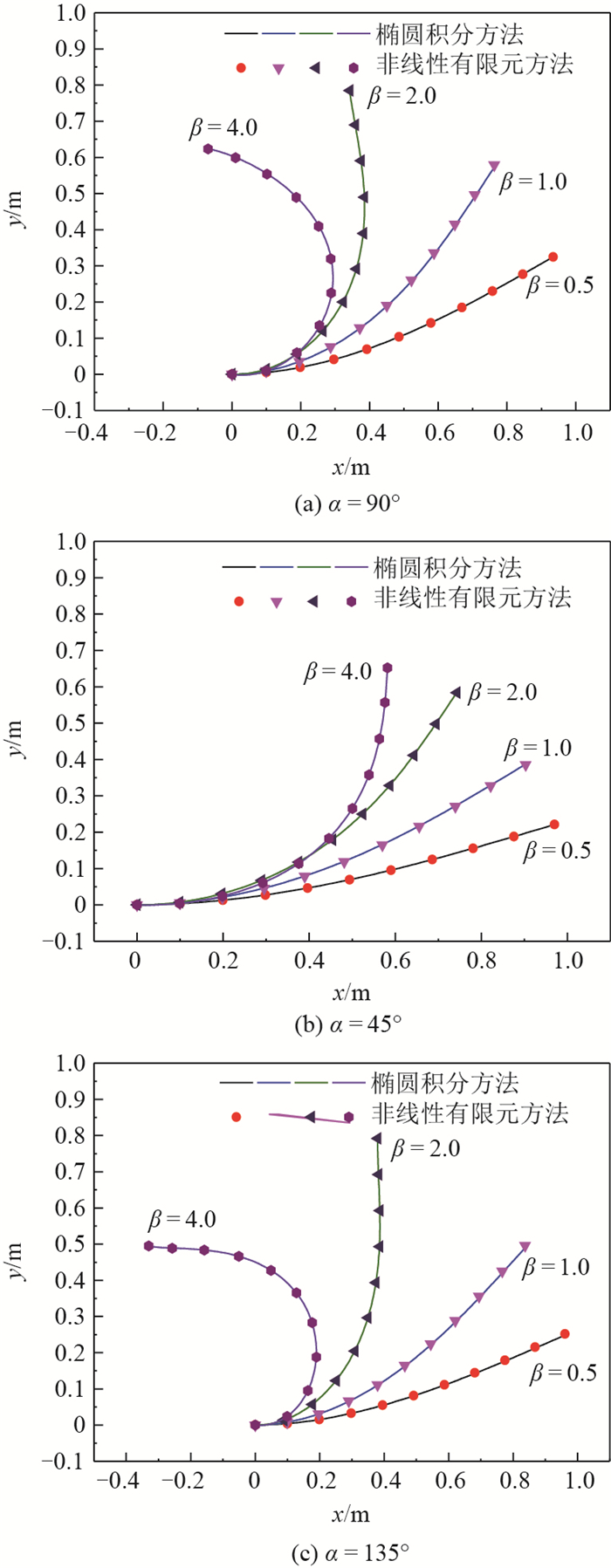
参数	数值
长度L/m	1
截面半径r/m	0.001 7
弹性模量E/(N·m^-2)	7×10¹⁰
泊松比	0.29

下载: 导出CSV

表 2 定向载荷下梁端部变形δ对比

Table 2. Contrast of beam end deflection δ with dead force

载荷方位角/(°)	载荷因子	椭圆积分解/m	有限元解/m	偏差/%
90	0.5	0.301 63	0.301 81	0.06
90	1.0	0.493 5	0.494 96	0.3
90	2.0	0.670 65	0.671 49	0.12
90	4.0	0.787 85	0.788 11	0.03
45	0.5	0.295 45	0.295 58	0.04
45	1.0	0.582 65	0.584 92	0.39
45	2.0	0.797 67	0.798 19	0.65
45	4.0	0.847 02	0.843 12	0.46
135	0.5	0.178 43	0.178 44	0.01
135	1.0	0.280 25	0.281 05	0.28
135	2.0	0.388 11	0.388 32	0.05
135	4.0	0.480 46	0.480 58	0.02

下载: 导出CSV

表 3 随动载荷下梁端部变形δ对比

Table 3. Contrast of beam end deflection δ with follower force

载荷方位角/(°)	载荷因子	椭圆积分解/m	有限元解/m	偏差/%
90	0.5	0.324 8	0.324 64	0.05
90	1.0	0.576 22	0.579 23	0.52
90	2.0	0.785 65	0.784 63	0.13
90	4.0	0.623 69	0.623 01	0.11
45	0.5	0.221 02	0.221 0	0.01
45	1.0	0.386 93	0.385 97	0.25
45	2.0	0.584 41	0.583 68	0.12
45	4.0	0.652 39	0.651 96	0.15
135	0.5	0.252 09	0.252 06	0.01
135	1.0	0.492 37	0.496 02	0.74
135	2.0	0.793 19	0.792 17	0.13
135	4.0	0.495 42	0.495 06	0.07

下载: 导出CSV

参考文献(19)

[1]	DADO M, AL-SADDER S. A new technique for large deflection analysis of non-prismatic cantilever beams[J]. Mechanics Research Communications, 2005, 32(6): 692-703. doi: 10.1016/j.mechrescom.2005.01.004
[2]	BISSHOP K E, DRUCKER D C. Large deflection cantilever beams[J]. Quarterly of Applied Mathematics, 1945, 3(3): 272-275. doi: 10.1090/qam/13360
[3]	TIMOSHENKO S P, GERE J M. Theory of elastic stability[M]. New York: McGraw-Hill, 1963: 125-127.
[4]	RAO B N, RAO G V. Applicability of static and dynamic criterion for the stability of a cantilever column under a tip-concentrated subtangential follower force[J]. Journal of Sound and Vibration, 1987, 120(1): 197-200. http://www.sciencedirect.com/science/article/pii/0022460X88903458
[5]	WANG C M, KITIPORNCHAI S. Shooting optimization technique for large deflection analysis of structural members[J]. Engineering Structure, 1992, 14(4): 231-240. doi: 10.1016/0141-0296(92)90011-E
[6]	SRPCIC S, SAJE M. Large deflections of thin curved plane beam of constant initial curvature[J]. International Journal of Mechanical Science, 1986, 28(5): 275-287. doi: 10.1016/0020-7403(86)90041-X
[7]	WANG G, SHAHINPOOR M. Design prototyping and computer simulations of a novel large bending actuator made with a shape memory alloy contractile wire[J]. Smart Materials Structure, 1996, 6(2): 214-221. http://adsabs.harvard.edu/abs/1997SMaS....6..214W
[8]	ARGYRIS J H, SYMEONIDS S P. Non-linear finite element analysis of elastic systems under nonconservative loading-natural formulation. Part 1. Quasi-static problems[J]. Compute Methods of Applied Mechanical Engineering, 1981, 26(1): 75-123. doi: 10.1016/0045-7825(81)90131-6
[9]	HOWELL L L, MIDHA A. Parametric deflection approximations for end-loaded large deflection beams in compliant mechanic[J]. Journal of Mechanical Design, 1995, 117(1): 156-165. doi: 10.1115/1.2826101
[10]	KIMBALL C, TSAI L W. Modeling of flexural beams subjected to arbitrary end loads[J]. Journal of Mechanical Design, 2002, 124(2): 223-234. doi: 10.1115/1.1455031
[11]	LAU J H. Closed-form solutions for the large deflections of curved optical glass fibers under combined loads[J]. Journal of Electron Package, 1993, 115(3): 337-339. doi: 10.1115/1.2909337
[12]	SHINOHARA A, HARA M. Large deflection of a circular c-shaped spring[J]. International Journal of Mechanical Science, 1979, 21(3): 179-186. doi: 10.1016/0020-7403(79)90022-5
[13]	王恩惠. 弹性悬臂杆的平衡分支[J]. 固体力学学报, 1983, 4: 143-151. https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX198304014.htm WANG E H. Balance branch of elastic cantilever rod[J]. Acta Mechanica Solida Sinica, 1983, 4: 143-151(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX198304014.htm
[14]	李银山, 刘波, 潘文波, 等. 弹性压杆的大变形分析[J]. 河北工业大学学报, 2011, 40(5): 31-35. doi: 10.3969/j.issn.1007-2373.2011.05.007 LI Y S, LIU B, PAN W B, et al. Analysis of large deflection of flexible compression bars[J]. Journal of Hebei University of Technology, 2011, 40(5): 31-35(in Chinese). doi: 10.3969/j.issn.1007-2373.2011.05.007
[15]	FRISCH-FAY R. Flexible bars[M]. London: Butterworths, 1962: 119-151.
[16]	RAO B N, RAO G V. Applicability of static or dynamic criterion for the stability of a non-uniform cantilever column subjected to a tip-concentrated subtangential follower force[J]. Journal of Sound and Vibration, 1988, 122(1): 188-191. doi: 10.1016/S0022-460X(88)80017-8
[17]	NAVAEE S, ELLING R. Equilibrium configurations of cantilever beams subjected to inclined end loads[J]. Journal of Applied Mechanics, 1992, 59(3): 572-579. doi: 10.1115/1.2893762
[18]	SHAVARTSMAN B S. Large deflections of cantilever beam subjected to a follower force[J]. Journal of Sound and Vibration, 2007, 304(3-5): 969-973. doi: 10.1016/j.jsv.2007.03.010
[19]	王竹溪, 郭敦仁. 特殊函数概论[M]. 北京: 北京大学出版社, 2000: 520-556. WANG Z X, GUO D R. Special functions[M]. Beijing: Peking University Press, 2000: 520-556(in Chinese).