-
摘要:
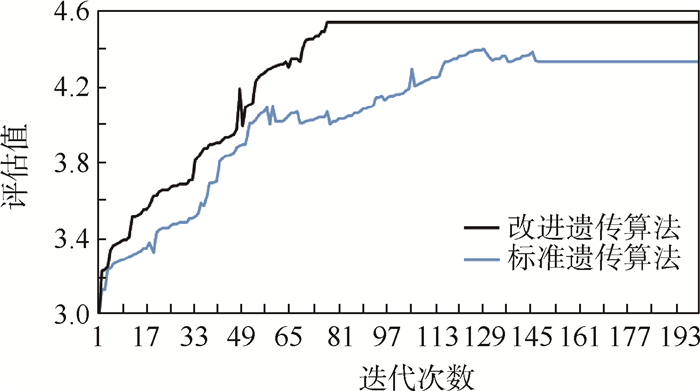
针对标准遗传算法求解装载方案时存在收敛速度慢、易早熟、寻优结果欠佳的问题，基于拟人装载策略，提出了一种以集装箱空间利用率最大为目标，考虑货物装载顺序、体积、质量、重心、不重叠等多种实际约束的改进遗传算法。首先，采用与货物放置状态相结合的实数编码，随机产生初始种群；然后，在常规选择操作中加入最优解保存策略，并将稳定性、支撑限制、重心约束考虑到进行线性尺度变换后的适应度函数中，以此来计算每种装载方案的评估值；最后，输出评估值最高的方案作为最优装载方案。实验采用异构性不同的测试算例进行性能测试，结合3组具体货物装载数据证明算法的普适性与实用性。结果表明：所提算法在求解强异构货物装载过程中具有较好的优化效果，适用于求解集装箱装载问题。与标准遗传算法相比，收敛性与搜索速度有所提高，2种不同箱型的集装箱空间利用率分别提高了3.82%和3.66%，运行时间分别缩短了7.9 s和5.58 s，能快速找到最优装载方案，可有效解决规则、不规则集装箱的货物装箱问题。基于MATLAB软件实现装载方案的可视化，为集装箱的实时装载决策提供了理论基础。
Abstract:Aimed at the problems of slow convergence speed, premature maturity, and poor optimization results when the standard genetic algorithm solves the loading plan, based on the anthropomorphic loading strategy, an improved genetic algorithm is proposed to maximize the utilization of container space, considering the loading sequence, volume, and quality of the goods, center of gravity, non-overlapping and other practical constraints. First, the real number code combined with the placement state of the goods is used to randomly generate the initial population. Second, the optimal solution preservation strategy is added to the routine selection operation, and the stability, support constraints, and center of gravity constraints are taken into account after linear scale transformation. In the fitness function, the evaluation value of each loading scheme is calculated by this. Finally, the scheme with the highest evaluation value is output as the optimal loading scheme. In the experimental part, the performance test was performed using test cases with different heterogeneity, and then three sets of specific cargo loading data were combined to prove the universality and practicability of the algorithm. The results show that the proposed algorithm has better optimization effect in solving the process of strong heterogeneous cargo loading, and is suitable for solving the container loading problem. Compared with the standard genetic algorithm, the convergence and search speed have been improved. The space utilization of the two different container types has increased by 3.82% and 3.66%, and the running time has been shortened by 7.9 s and 5.58 s. The optimal loading can be found quickly. The solution can effectively solve the problem of cargo packing in regular and irregular containers. At the same time, the visualization of the loading plan is realized based on MATLAB software, which provides a theoretical basis for the real-time loading decision of the container.
-
表 1 算例测试结果对比
Table 1. Comparison of example test results
货物特征 编号 长 宽 高 平均空间利用率/% 混合免疫遗传算法 改进遗传算法 2个尺寸相同 1 200 160 80~160 96.34 95.89 2 200 100~200 100 91.92 92.43 3 160~320 160 100 87.71 88.26 1个尺寸相同 4 200 100~200 50~100 86.20 89.13 5 140~280 140 50~100 83.20 86.56 6 120~240 80~160 80 82.94 85.54 无尺寸相同 7 200~300 160~240 80~120 82.16 84.47 8 200~400 160~320 80~160 72.75 80.11 
下载: 导出CSV
表 2 集装箱参数
Table 2. Container parameters
箱型 尺寸/cm 可载重量/kg 适载机型 AMA集装箱 {w,h,d}={318,214,214} 6 444 747F AKE集装箱 {w1,w2,h,d}={201,156,154,163} 1 488 747、777、747F
下载: 导出CSV
表 3 货物基本参数
Table 3. Basic cargo parameters
参数 第1组 第2组 第3组 平均长度/cm 65.32 51.56 45.74 平均宽度/cm 50.21 44.47 36.98 平均高度/cm 57.96 52.53 46.32 平均质量/kg 46.56 37.18 23.27 货物件数 50 100 150
下载: 导出CSV
表 4 不同箱型2种算法的对比结果
Table 4. Comparison results of two algorithms for different container types
箱型 货物实验组 标准遗传算法 改进遗传算法 平均空间利用率/% 平均装载货物件数 平均运行时间/s 平均空间利用率/% 平均装载货物件数 平均运行时间/s AMA集装箱 第1组 85.21 37 18.54 88.45 40 10.43 第2组 85.89 75 29.37 89.89 80 19.65 第3组 86.75 104 33.41 90.97 110 27.56 平均 85.95 72 27.11 89.77 77 19.21 AKE集装箱 第1组 84.66 22 12.53 87.67 25 6.28 第2组 84.98 36 19.12 88.84 40 15.79 第3组 85.29 49 25.63 89.42 55 18.45 平均 84.98 36 19.09 88.64 40 13.51
下载: 导出CSV
-
[1] RAMOS A G, SILVA E, OLIVEIRA J F. A new load balance methodology for container loading problem in road transportation[J]. European Journal of Operational Research, 2018, 266(3): 1140-1152. doi: 10.1016/j.ejor.2017.10.050 [2] MAXENCE D, MANUEL I. Enhanced pseudo-polynomial formulations for bin packing and cutting stock problems[J]. Informs Journal on Computing, 2020, 32(1): 101-119. doi: 10.1287/ijoc.2018.0880 [3] 刘胜, 沈大勇, 商秀芹, 等. 求解三维装箱问题的多层树搜索算法[J]. 自动化学报, 2020, 46(6): 1178-1187. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO202006008.htmLIU S, SHEN D Y, SHANG X Q, et al. Multi-layer tree search algorithm for solving three-dimensional packing problem[J]. Journal of Automation, 2020, 46(6): 1178-1187(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO202006008.htm [4] LIU S, TAN W, XU Z, et al. A tree search algorithm for the container loading problem[J]. Computers & Industrial Engineering, 2014, 75: 20-30. [5] ALINE A S, FRANKLINA M B, TOLEDO J, et al. Irregular packing problems: A review of mathematical models[J]. European Journal of Operational Research, 2020, 282(3): 803-822. doi: 10.1016/j.ejor.2019.04.045 [6] MAURO D, FABIO F, MANUEL I. A branch-and-price algorithm for the temporal bin packing problem[J]. Computers and Operations Research, 2020, 114: 1-16. http://www.sciencedirect.com/science/article/pii/S0305054819302679 [7] YU F, AMARNATH B. Heuristic/meta-heuristic methods for restricted bin packing problem[J]. Journal of Heuristics, 2020, 26: 637-662. doi: 10.1007/s10732-020-09444-y [8] 何琨, 黄文奇. 基于动作空间的三维装箱问题的确定性高效率求解算法[J]. 计算机学报, 2014, 37(8): 1786-1793. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201408013.htmHE K, HUANG W Q. A deterministic and efficient solution algorithm for the three-dimensional packing problem based on action space[J]. Journal of Computer Science, 2014, 37(8): 1786-1793(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201408013.htm [9] 何琨, 黄文奇, 胡骞. 基于动作空间的求解三维矩形装箱问题的穴度算法[J]. 计算机科学, 2010, 37(10): 181-183. doi: 10.3969/j.issn.1002-137X.2010.10.042HE K, HUANG W Q, HU Q. Acuity algorithm for solving three-dimensional rectangular boxing problem based on action space[J]. Computer Science, 2010, 37(10): 181-183(in Chinese). doi: 10.3969/j.issn.1002-137X.2010.10.042 [10] 何琨, 黄文奇. 三维矩形Packing问题的拟人求解算法[J]. 中国科学: 信息科学, 2010, 40(12): 1586-1595. https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201012004.htmHE K, HUANG W Q. Anthropomorphic algorithm for solving three-dimensional rectangular Packing problems[J]. Science in China: Information Science, 2010, 40(12): 1586-1595(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201012004.htm [11] 崔会芬, 许佳瑜, 朱鸿国, 等. 基于改进遗传算法的三维单箱装箱问题研究[J]. 工业工程与管理, 2018, 23(1): 86-89. https://www.cnki.com.cn/Article/CJFDTOTAL-GYGC201801014.htmCUI H F, XU J Y, ZHU H G, et al. Research on three-dimensional single box packing based on improved genetic algorithm[J]. Industrial Engineering and Management, 2018, 23(1): 86-89(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GYGC201801014.htm [12] 张钧, 贺可太. 求解三维装箱问题的混合遗传模拟退火算法[J]. 计算机工程与应用, 2019, 55(14): 32-39. doi: 10.3778/j.issn.1002-8331.1902-0127ZHANG J, HE K T. Hybrid genetic simulated annealing algorithm for solving the three-dimensional packing problem[J]. Computer Engineering and Applications, 2019, 55(14): 32-39(in Chinese). doi: 10.3778/j.issn.1002-8331.1902-0127 [13] MENGHANI D, GUHA A. Packing boxes into multiple containers using genetic algorithm[J]. Journal of the Institution of Engineers (India): Series C, 2016, 97(3): 441-450. doi: 10.1007/s40032-016-0285-2 [14] 代爱民. 基于混合免疫遗传算法的半在线三维装箱问题研究[D]. 重庆: 重庆大学, 2018.DAI A M. Research on semi-online 3D packing problem based on hybrid immune genetic algorithm[D]. Chongqing: Chongqing University, 2018(in Chinese). [15] 于明正, 徐斌, 陈佳. 基于双层启发式遗传算法的三维装箱问题[J]. 科学技术与工程, 2020, 20(5): 2042-2047. doi: 10.3969/j.issn.1671-1815.2020.05.050YU M Z, XU B, CHEN J. Three-dimensional packing problem based on double-layer heuristic genetic algorithm[J]. Science Technology and Engineering, 2020, 20(5): 2042-2047(in Chinese). doi: 10.3969/j.issn.1671-1815.2020.05.050 [16] 李鹏, 汤勇. 三维货物装箱问题的研究进展[J]. 铁道科学与工程学报, 2015, 12(5): 1232-1242. doi: 10.3969/j.issn.1672-7029.2015.05.037LI P, TANG Y. Research progress of three-dimensional cargo packing[J]. Journal of Railway Science and Engineering, 2015, 12(5): 1232-1242(in Chinese). doi: 10.3969/j.issn.1672-7029.2015.05.037 [17] 张德富, 魏丽军, 陈青山, 等. 三维装箱问题的组合启发式算法[J]. 软件学报, 2007, 18(9): 2083-2089. https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB200709005.htmZHANG D F, WEI L J, CHEN Q S, et al. Combined heuristic algorithm for three-dimensional packing problem[J]. Journal of Software, 2007, 18(9): 2083-2089(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB200709005.htm [18] RUDOLPH G. Convergence analysis of canonical GA[J]. IEEE Trans on Neural Networks, 1994, 5(1): 96-101. doi: 10.1109/72.265964 -
下载:
点击查看大图
计量
- 文章访问数: 775
- HTML全文浏览量: 116
- PDF下载量: 147
- 被引次数: 0
