-
摘要:
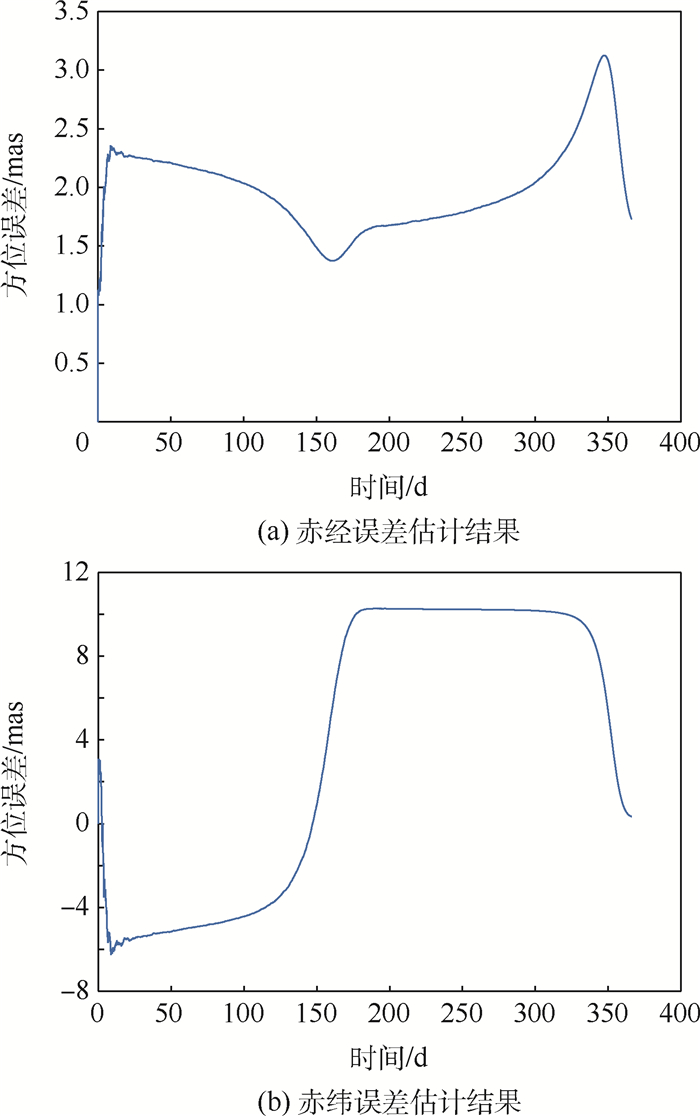
为了克服钟差和卫星位置误差对脉冲星方位误差估计的影响，设计了两步卡尔曼滤波（TSKF）算法。首先，介绍了脉冲星方位误差估计的传统模型，并通过分析和仿真验证了钟差、卫星位置误差以及2种误差同时存在时会使脉冲星方位误差估计结果产生较大偏差。其次，在传统的估计模型中加入了钟差和卫星位置误差，并将钟差和钟差变化率增广为新的状态量，从而推导出包含2种误差的新模型，并证明了该模型的完全可观测性；根据该模型并按照两步卡尔曼滤波原理，得到了TSKF算法的步骤。最后，通过仿真表明：在钟差和卫星位置误差同时影响下，传统脉冲星方位误差估计算法偏差较大且发散；TSKF算法则能够有效隔离2种误差的影响，使赤经和赤纬误差估计达到0.2 mas之内的精度。
-
关键词:
- 方位误差 /
- 时钟钟差 /
- 卫星位置误差 /
- 增广状态 /
- 两步卡尔曼滤波(TSKF)
Abstract:A Two-Step Kalman Filter (TSKF) algorithm is designed to overcome the influence of clock error and satellite position error on pulsar position error estimation. First, the traditional model of pulsar position error estimation is introduced, and it is confirmed by analysis that the clock error, satellite position error, and both errors will have serious impact on the estimation. Second, the clock error and satellite position error are added to the traditional estimation model, and the clock error and its rate of change are expanded to a new state quantity, thereby deducing a new model of pulsar position error estimation containing these two errors. And its observability is proved through theoretical analysis. Then the update equation of the TSKF algorithm is written combined with the new model and based on the two-step Kalman filter principle. Finally, simulations show that the TSKF algorithm can effectively isolate the influences of the two errors and make the estimation accuracy kept within 0.2 mas while the traditional pulsar position error estimation algorithm has a large deviation and divergence of the right ascension and declination errors under the influence of the two errors.
-
图 4 未修正卫星位置误差的估计结果
Figure 4. Estimation results with uncorrected satellite position errors
表 1 脉冲星B0531+21参数
Table 1. Parameters of pulsar B0531+21
参数 数值 赤经/(°) 83.63 赤纬/(°) 22.01 距离/kpc 2.0 P/ms 33.4 W/ms 1.7 Fx/(ph·cm－2·s－1) 1.54 pf/% 70 注：kpc为秒差距，是天文学中使用的距离单位；ph·cm－2·s－1为宇宙背景噪声单位。 
下载: 导出CSV
表 2 卫星轨道参数
Table 2. Parameters of satellite orbit
参数 数值 半长轴/km 7 460 离心率 4.55×10-16 轨道倾角/(°) 25 近地点幅角/(°) 45 升交点赤经/(°) 0 初始真近地点/(°) 30 起始时间 2015-07-01T12：00：00
下载: 导出CSV
表 3 条件设置
Table 3. Condition setup
钟差/(μs) 卫星位置误差/km 0 (0.1, 0.1, 0.1) 1 (0, 0, 0) 1 (0.1，-0.1，0.1) 2 (0.1, 0.1, 0.1) 2 (0.2，-0.2, 0.2) 2 (0.5, 0.5, 0.5) 5 (0.1, 0.1, 0.1) 5 (0.2，-0.2, 0.2)
下载: 导出CSV
表 4 仿真结果
Table 4. Simulation results
赤经估计偏差/mas 赤纬估计偏差/mas 0.050 0.043 0.061 0.047 0.150 0.065 0.150 0.072 0.172 0.110 0.221 0.150 0.182 0.143
下载: 导出CSV
-
[1] SHEIKH S I. The use of variable celestial X-ray sources for spacecraft navigation[D]. Maryland: University of Maryland, 2005. [2] 刘劲. 基于X射线脉冲星的航天器自主导航方法研究[D]. 武汉: 华中科技大学, 2011.LIU J. X-ray pulsar-based spacecraft autonomous navigation[D]. Wuhan: Huazhong University of Science and Technology, 2011(in Chinese). [3] 孙守明. 基于X射线脉冲星的航天器自主导航方法研究[D]. 长沙: 国防科学技术大学, 2011.SUN S M. Study on autonomous navigation method of spacecraft based on X-ray pulsars[D]. Changsha: National University of Defense Technology, 2011(in Chinese). [4] 孙守明, 郑伟, 汤国建. X射线脉冲星星表方位误差估计算法研究[J]. 飞行器测控学报, 2010, 29(2): 57-60. https://www.cnki.com.cn/Article/CJFDTOTAL-FXCK201002017.htmSUN S M, ZHENG W, TANG G J. A new estimation algorithm of the X-ray pulsar position error[J]. Journal of Spacecraft TT & C Technology, 2010, 29(2): 57-60(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FXCK201002017.htm [5] 熊凯, 魏春岭, 刘良栋. 鲁棒滤波技术在脉冲星导航中的应用[J]. 空间控制技术与应用, 2008, 34(6): 8-11. https://www.cnki.com.cn/Article/CJFDTOTAL-KJKZ200806004.htmXIONG K, WEI C L, LIU L D. Application of robust filtering in pulsars-based navigation[J]. Aerospace Control and Application, 2008, 34(6): 8-11(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KJKZ200806004.htm [6] XU Q, WANG H L, FENG L, et al. An improved augmented X-ray pulsar navigation algorithm based on the norm of pulsar direction error[J]. Advances in Space Research, 2018, 62(11): 3187-3198. doi: 10.1016/j.asr.2018.08.026 [7] NING X L, GUI M Z, FANG J C, et al. Differential X-ray pulsar aided celestial navigation for Mars exploration[J]. Aerospace Science and Technology, 2017, 62: 36-45. doi: 10.1016/j.ast.2016.10.032 [8] 王宏力, 许强, 由四海, 等. 考虑卫星位置误差的增广脉冲星方位误差估计算法[J]. 国防科技大学学报, 2018, 40(5): 177-182. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201805026.htmWANG H L, XU Q, YOU S H, et al. Augmented estimation algorithm for pulsar position error with satellite position error[J]. Journal of National University of Defense Technology, 2018, 40(5): 177-182(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201805026.htm [9] 孙守明, 郑伟, 汤国建. X射线脉冲星/SINS组合导航中的钟差修正方法研究[J]. 国防科技大学学报, 2010, 32(6): 82-86. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201006016.htmSUN S M, ZHENG W, TANG G J. A new clock error control algorithm of X-ray pulsars/SINS integrated navigation[J]. Journal of National University of Defense Technology, 2010, 32(6): 82-86(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201006016.htm [10] 王璐, 史晨曦, 李建勋, 等. 考虑钟差修正的脉冲星与多普勒差分组合导航[J]. 电波科学学报, 2018, 33(2): 217-224. https://www.cnki.com.cn/Article/CJFDTOTAL-DBKX201802016.htmWANG L, SHI C X, LI J X, et al. Pulsar and Doppler difference integrated navigation considering clock error control[J]. Chinese Journal of Radio Science, 2018, 33(2): 217-224(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DBKX201802016.htm [11] EMADZADEH A A, SPEYER J L. X-ray pulsar-based relative navigation using epoch folding[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2317-2328. http://ieeexplore.ieee.org/document/6034635 [12] 李孝辉, 吴海涛, 高海军, 等. 用Kalman滤波器对原子钟进行控制[J]. 控制理论与应用, 2003, 20(4): 551-554. https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY200304013.htmLI X H, WU H T, GAO H J, et al. Clock disciplined method by using Kalman filter[J]. Control Theory & Applications, 2003, 20(4): 551-554(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY200304013.htm [13] 帅平, 陈绍龙, 吴一帆, 等. X射线脉冲星导航技术研究进展[J]. 空间科学学报, 2007, 27(2): 169-176. https://www.cnki.com.cn/Article/CJFDTOTAL-KJKB200702013.htmSHUAI P, CHEN S L, WU Y F, et al. Advance in X-ray pulsar navigation technology[J]. Chinese Journal of Space Science, 2007, 27(2): 169-176(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KJKB200702013.htm [14] FRIEDLAND B. Treatment of bias in recursive filtering[J]. IEEE Transactions on Automatic Control, 1969, 14(4): 359-367. http://ieeexplore.ieee.org/document/1099223/references [15] HAESSIG D, FRIEDLAND B. Separate-bias estimation with reduced-order Kalman filters[J]. IEEE Transactions on Automatic Control, 1998, 43(7): 983-987. http://ieeexplore.ieee.org/iel4/9/15074/00701106.pdf [16] IGNAGNI M B. Separate bias Kalman estimator with bias state noise[J]. IEEE Transactions on Automatic Control, 1990, 35(3): 338-341. http://ieeexplore.ieee.org/document/50352 [17] 王奕迪, 郑伟, 孙守明, 等. 考虑系统偏差的脉冲星守时算法研究[J]. 国防科技大学学报, 2013, 35(2): 12-16. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201302004.htmWANG Y D, ZHENG W, SUN S M, et al. Algorithm for the pulsar timing system with the system bias[J]. Journal of National University of Defense Technology, 2013, 35(2): 12-16(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ201302004.htm [18] 许强, 范小虎, 徐利国, 等. 脉冲星方位误差估计的TSKF算法[J]. 北京航空航天大学学报, 2020, 46(4): 761-768. doi: 10.13700/j.bh.1001-5965.2019.0288XU Q, FAN X H, XU L G, et al. TSKF algorithm for pulsar position error estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(4): 761-768(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0288 -
下载:
点击查看大图
计量
- 文章访问数: 612
- HTML全文浏览量: 177
- PDF下载量: 41
- 被引次数: 0
