涂覆吸波材料圆柱的RCS预估方法

赵京城; 杨宗凯; 王健; 张扬

doi:10.13700/j.bh.1001-5965.2020.0214

涂覆吸波材料圆柱的RCS预估方法

doi: 10.13700/j.bh.1001-5965.2020.0214

赵京城^1, ,,
杨宗凯¹,
王健²,
张扬²

1.
北京航空航天大学电子信息工程学院, 北京 100083
2.
航空工业第一飞机设计研究院, 西安 710089

详细信息

通讯作者:
赵京城. E-mail: zjccool@126.com

中图分类号: TN951
计量
- 文章访问数: 520
- HTML全文浏览量: 50
- PDF下载量: 190
- 被引次数: 0
出版历程
- 收稿日期: 2020-05-25
- 录用日期: 2020-08-01
- 网络出版日期: 2021-07-20

RCS prediction method for cylinder containing microwave absorbing material

1.
School of Electronic and Information Engineering, Beihang University, Beijing 100083, China
2.
AVIC The First Aircraft Institute, Xi'an 710089, China

More Information

Corresponding author: ZHAO Jingcheng. E-mail: zjccool@126.com

摘要

摘要:
用缩比模型测量结果预估是研制阶段获得大尺寸目标雷达散射截面（RCS）的常用方法，但根据经典电磁相似理论，严格满足缩比条件的涂覆吸波材料缩比目标测量难以实现。针对涂覆吸波材料缩比目标的RCS预估问题，提出了采用多元对数线性回归模型的预估方法。设计了2组圆柱模型，在微波暗室中对缩比因子分别为1、2、4、8的2组模型进行了测试。在完成角度矫正等数据预处理基础上，将缩比模型RCS数据作为训练集代入模型当中求得参数，对原模型的RCS进行预估并与实际实测数据进行对比分析。结果表明：所提方法预估数据与实测数据曲线拟合度较好，相较于传统平方率模型，误差下降了3~5 dB，在回归模型中加入吸波材料因子后误差进一步下降了0.3~0.8 dB。
- 雷达散射截面(RCS) /
- 缩比模型 /
- 多元线性回归 /
- 吸波材料 /
- 相似原理
Abstract:
Large target's Radar Cross Section (RCS) estimation using scaling model is a common method to obtain RCS at the development phase. However, according to classical electromagnetic similarity theory, measurement of scaled target coated with microwave absorbing material is difficult to meet the scaling condition strictly. A multivariate logarithmic linear regression model is proposed to estimate RCS for the scaled target coated with microwave absorbing materials. Two sets of cylindrical models were designed and tested in the microwave anechoic chamber with scaling factors of 1:1, 1:2, 1:4 and 1:8, respectively. On the basis of data preprocessing such as angle correction, RCS data of scaling model is substituted into the model as training set to obtain parameters, and RCS of the original model is estimated and compared with the actual measured data. The results show that the curves of the predicted data and the measured data fit well. Compared with the traditional square rate formula, the error of the proposed method decreases by 3-5 dB, and the error decreases by 0.3-0.8 dB after adding the microwave absorbing material factor to the regression model.
- Radar Cross Section (RCS) /
- scaling model /
- multiple linear regression /
- microwave absorbing material /
- similarity principle

HTML全文

图 1 吸波材料反射率随频率变化

Figure 1. Reflectance of microwave absorbing materials varies with frequency

下载: 全尺寸图片幻灯片

图 2 测试场地示意图

Figure 2. Sketch map of test site

下载: 全尺寸图片幻灯片

图 3 两种圆柱模型的设计图

Figure 3. Design drawing of two kinds of cylinder model

下载: 全尺寸图片幻灯片

图 4 实际测试示意图

Figure 4. Sketch map of actual test

下载: 全尺寸图片幻灯片

图 5 测试及数据处理流程

Figure 5. Flowchart of test and data processing

下载: 全尺寸图片幻灯片

图 6 测试频率1.835 GHz下圆柱1单站RCS对角度曲线

Figure 6. Influence of angle on cylinder 1's monostatic RCS with test frequency of 1.835 GHz

下载: 全尺寸图片幻灯片

图 7 不同缩比因子模型的角度偏差统计对比

Figure 7. Comparison of angle deviation of models with different scaling factors

下载: 全尺寸图片幻灯片

图 8 圆柱1不同模型下单站RCS预估与实测对比

Figure 8. Comparison of prediction and measurement of cylinder 1's monostatic RCS in different models

下载: 全尺寸图片幻灯片

图 9 圆柱2不同模型下单站RCS预估与实测对比

Figure 9. Comparison of prediction and measurement of cylinder 2's monostatic RCS in different models

下载: 全尺寸图片幻灯片

表 1 电磁相似原理条件

Table 1. Conditions of electromagnetic similarity principle

物理量	原模型	缩比模型
长度	l	l′=l/n
频率	f	f′=nf
波长	λ	λ′=λ/n
电导率	σ	σ′=nσ
磁导率	μ	μ′=μ
介电常数	ε	ε′=ε
表面阻抗	η	η′=η

下载: 导出CSV

表 2 圆柱1的尺寸及测试频率

Table 2. Dimension and test frequency of cylinder 1

n	长度/mm	直径/mm	测试频率/GHz	组数
0.96	2 092	159	1.5~2	101
2	1 000	76	3.5~4.5	201
4	500	38	7~9	401
8	250	19	14~18	801

下载: 导出CSV

表 3 圆柱2的尺寸及测试频率

Table 3. Dimension and test frequency of cylinder 2

n	长度/mm	直径/mm	测试频率/GHz	组数
1	480.0	240	2~2.5	101
2	240	120	3.5~4.5	201
4	120	60	7~9	401
8	60	30	14~18	801

下载: 导出CSV

表 4 测量误差与目标和背景电平的差值典型数据

Table 4. Typical data of measurement error according to difference of target and background ratio

	测量误差/dB
31	±0.25
25	±0.5
19	±1
16	±1.5
10.69	±3

下载: 导出CSV

表 5 圆柱1数据角度校准结果

Table 5. Calibration results of angle of cylinder 1 (°)

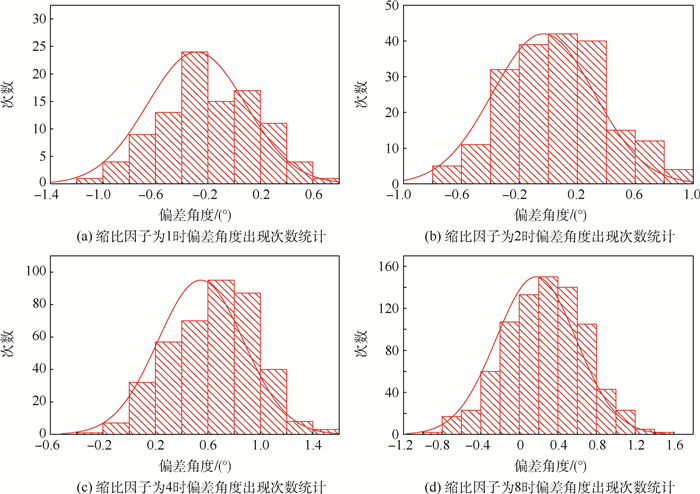
极化方式	n=0.96	n=2	n=4	n=8
HH	-0.6	0.2	-0.2	-0.2
VV	-0.6	0	-0.2	0.4

下载: 导出CSV

表 6 圆柱2数据角度校准结果

Table 6. Calibration results of angle of cylinder 2 (°)

极化方式	n=1	n=2	n=4	n=8
HH	0.2	0.2	0.2	0.8
VV	0	0.2	0.4	-0.2

下载: 导出CSV

表 7 圆柱1的模型1摘要(HH极化)

Table 7. Model one's summary of cylinder 1(HH polarization)

R	R²	调整后的R²	标准估算的误差
0.980	0.961	0.961	1.602 808

下载: 导出CSV

表 8 圆柱1的模型1回归方程系数(HH极化)

Table 8. Model one's regression equation coefficients of cylinder 1 (HH polarization)

因子	系数	标准错误	t	显著性
x₁	0.943	0	2 830.873	0
x₂	27.175	0.041	967.286	0

下载: 导出CSV

表 9 圆柱1不同模型回归公式与平均绝对误差对比

Table 9. Comparison of regression formula and absolute error of cylinder 1 in different models

极化方式	模型	回归公式	相关系数	拟合度	平均绝对误差/dB
HH极化	传统平方率模型	y=x₁+20x₂	0.927	0.859	4.93
HH极化	模型1	y=0.943x₁+27.175x₂	0.980	0.961	1.94
HH极化	模型2	y=0.996x₁+21.279x₂-0.08x₃-0.708x₄	0.998	0.995	1.11
VV极化	传统平方率模型	y=x₁+20x₂	0.934	0.872	5.26
VV极化	模型1	y=0.991x₁+30.630x₂	0.992	0.984	2.14
VV极化	模型2	y=1.039x₁+19.476x₂-1.728x₃-0.378x₄	0.994	0.988	1.29

下载: 导出CSV

表 10 圆柱2不同模型回归公式与平均绝对误差对比

Table 10. Comparison of regression formula and absolute error of cylinder 2 in different models

极化方式	模型	回归公式	相关系数	拟合度	平均绝对误差/dB
HH极化	传统平方率模型	y=x₁+20x₂	0.934	0.872	7.18
HH极化	模型1	y=0.969x₁+33.130x₂	0.996	0.992	2.30
HH极化	模型2	y=0.964x₁+26.455x₂+0.355x₃-0.483x₄	0.997	0.995	1.62
VV极化	传统平方率模型	y=x₁+20x₂	0.946	0.895	5.92
VV极化	模型1	y=1.005x₁+30.119x₂	0.989	0.979	2.41
VV极化	模型2	y=0.969x₁+19.469x₂+0.046x₃-0.894x₄	0.991	0.982	2.18

下载: 导出CSV

参考文献(21)

[1]	VAN SCHALKWYK R F, SMIT J C. Dynamic radar cross section measurements of a full-scale aircraft for RCS modelling validation[C]//International Conference on Radar Systems (Radar 2017), 2017: 1-6.
[2]	李江海, 孙秦. 导体与非导体介质翼型的缩比模型RCS数值计算分析[J]. 航空计算技术, 2008, 38(1): 23-25. doi: 10.3969/j.issn.1671-654X.2008.01.007 LI J H, SUN Q. RCS numerical analysis of scaling model for conductor and nonconductor dielectric airfoil[J]. Aeronautical Computing Technology, 2008, 38(1): 23-25(in Chinese). doi: 10.3969/j.issn.1671-654X.2008.01.007
[3]	夏应清, 杨河林, 鲁述, 等. 超电大复杂目标RCS缩比模型预估方法[J]. 微波学报, 2003, 19(1): 8-11. doi: 10.3969/j.issn.1005-6122.2003.01.002 XIA Y Q, YANG H L, LU S, et al. Prediction of RCS for extremely large electric size target by using scaling model[J]. Chinese Journal of Radio Science, 2003, 19(1): 8-11(in Chinese). doi: 10.3969/j.issn.1005-6122.2003.01.002
[4]	陈晓洁, 李磊, 史小卫, 等. 半空间理想导体目标RCS缩比关系的研究[C]//全国微波毫米波会议, 2006: 96-99. CHEN X J, LI L, SHI X W, et al. Study on RCS scaling relationship of perfect conducting objects in half space[J]. National Conference on Microwave and Millimeter Waves (NCMMW), 2006: 96-99(in Chinese).
[5]	赵佼. 导体目标与海面复合电磁散射的缩比诱导关系[D]. 西安: 西安电子科技大学, 2014: 16-18. ZHAO J. The scale relation of the composite electromagnetic scattering from a conductor target above sea surface[D]. Xi'an: Xi'an University of Electronic Science and Technology, 2014: 16-18(in Chinese).
[6]	李良超, 吴振森, 邓蓉. 复杂目标后向激光雷达散射截面计算与缩比模型测量比较[J]. 中国激光, 2005, 32(6): 44-48. LI L C, WU Z S, DENG R. Comparison of the back laser rader cross-section calculation of complex object with the measurement of scale-model[J]. China Laser, 2005, 32(6): 44-48(in Chinese).
[7]	SHI Z D, DING C S, CHEN J Y. Dimensional analysis and physical similarity of lossy electromagnetic systems[J]. Chinese Physics Letters, 1993, 10(6): 347-350. doi: 10.1088/0256-307X/10/6/008
[8]	时振栋, 刘宏伟. 隐身目标雷达截面的缩比测量及反演计算[J]. 电子科技大学学报, 1995(S1): 13-17. SHI Z D, LIU H W. Scale measurement and inversion calculation of radar cross section of invisible target[J]. Journal of University of Electronic Science and Technology, 1995(S1): 13-17(in Chinese).
[9]	时振栋, 杨仕文, 丁春生. 有耗雷达目标散射截面的缩比计算——再论有耗电磁系统的相似性[J]. 应用科学学报, 1993, 11(2): 109-114. SHI Z D, YANG S W, DING C S. Computation of the scattering cross section of lossy radar targets-On the similarity of lossy electromagnetic systems[J]. Journal of Applied Sciences, 1993, 11(2): 109-114(in Chinese).
[10]	刘宏伟, 时振栋, 唐璞. 有耗雷达目标的RCS模型测量方法[J]. 电子科学学刊, 1996, 18(1): 95-98. LIU H W, SHI Z D, TANG P. RCS model measurement method for lossy radar targets[J]. Journal of Electronic Science, 1996, 18(1): 95-98(in Chinese).
[11]	胡艳, 时振栋, 唐璞, 等. 电磁相似性在计算基本散射体RCS方面的应用[J]. 应用科学学报, 2004, 22(1): 46-49. doi: 10.3969/j.issn.0255-8297.2004.01.010 HU Y, SHI Z D, TANG P, et al. The application of electromagnetic similarity in the calculation of RCS of the basic scatterer[J]. Journal of Applied Sciences, 2004, 22(1): 46-49(in Chinese). doi: 10.3969/j.issn.0255-8297.2004.01.010
[12]	陈晓洁. 电大目标雷达散射截面的研究[D]. 西安: 西安电子科技大学, 2006: 14-16. CHEN X J. Research on radar cross section of electrically large target[D]. Xi'an: Xi'an University of Electronic Science and Technology, 2006: 14-16(in Chinese).
[13]	蒋文亭, 吴德伟, 何晶. 目标雷达散射截面缩比测量关键技术概述[J]. 信息工程大学学报, 2013, 14(2): 184-188. JANG W T, WU D W, HE J. Summary of key technologies of scale model measurement of RCS[J]. Journal of Information Engineering University, 2013, 14(2): 184-188(in Chinese).
[14]	SUSETIO A, OKI T, MORISHITA H. Monostatic radar cross section evaluations of scale model single layer dielectric radar absorbing material at S and X bands[C]//IEEE 4th Asia-Pacific Conference on Antennas and Propagation (APCAP). Piscataway: IEEE Press, 2015: 568-569.
[15]	SINCLAIR G. Theory of models of electromagnetic systems[J]. Proceedings of the IRE, 1948, 36(11): 1364-1370. doi: 10.1109/JRPROC.1948.232289
[16]	刘闯, 金仁瀚, 巩二磊, 等. 多元线性回归方法预测燃气轮机发电机组性能[J]. 中国电机工程学报, 2017, 37(16): 4731-4738. LIU C, JIN R H, GONG E L, et al. Prediction for the performance of gas turbine units using multiple linear regression[J]. Proceedings of the CSEE, 2017, 37(16): 4731-4738(in Chinese).
[17]	王振友, 陈莉娥. 多元线性回归统计预测模型的应用[J]. 统计与决策, 2008(5): 46-47. WANG Z Y, CHEN L E. Application of multivariate linear regression statistical prediction model[J]. Statistics and Decision, 2008(5): 46-47(in Chinese).
[18]	黄兵, 胥云, 廖映华, 等. 基于BP神经网络和多元线性回归的航发叶片铣削力预测研究[J]. 机电工程, 2019, 36(8): 824-829. HUANG B, XU Y, LIAO Y H, et al. Milling force forecasting of aero-engine blade based on BP neural network and multivariate linear regression[J]. Journal of Mechanical & Electrical Engineering, 2019, 36(8): 824-829(in Chinese).
[19]	PERRON P, YAMAMOTO Y. Pitfalls of two-step testing for changes in the error variance and coefficients of a linear regression model[J]. Econometrics, 2019, 7(2): 1-11. http://ideas.repec.org/p/hit/econdp/2019-01.html
[20]	中国航天标准化研究所. 室内场目标雷达散射截面测试方法: GJB 5022-2001[S]. 北京: 国防科学技术工业委员会, 2001: 1-14. China Aerospace Standardization Institute. Method for measurement of radar cross section of scale target indoor range: GJB 5022-2001[S]. Beijing: Commission on Science, Technology and Industry for National Defense, 2001: 1-14(in Chinese).
[21]	李贵晓. 化工过程动态数据校正与过失误差侦破的研究[D]. 青岛: 青岛科技大学, 2014: 5-8. LI G X. Research on dynamic data correction and error detection of chemical process[D]. Qingdao: Qingdao University of Science and Technology, 2014: 5-8(in Chinese).