电动静液作动器的新型变阻尼级联滑模控制

王明康; 付永领; 赵江澳; 杨荣荣

doi:10.13700/j.bh.1001-5965.2020.0252

电动静液作动器的新型变阻尼级联滑模控制

doi: 10.13700/j.bh.1001-5965.2020.0252

1.
北京航空航天大学机械工程及自动化学院, 北京 100083
2.
兰州理工大学机电工程学院, 兰州 730050

详细信息

通讯作者:
付永领. E-mail: wmk_buaa@163.com

中图分类号: TH137
计量
- 文章访问数: 661
- HTML全文浏览量: 213
- PDF下载量: 82
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-11
- 录用日期: 2020-09-30
- 网络出版日期: 2021-08-20

Novel damping-variable sliding mode cascade control for electro-hydrostatic actuator

1.
School of Mechanical Engineering and Automation, Beihang University, Beijing 100083, China
2.
School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China

More Information

Corresponding author: FU Yongling. E-mail: wmk_buaa@163.com

摘要

摘要:
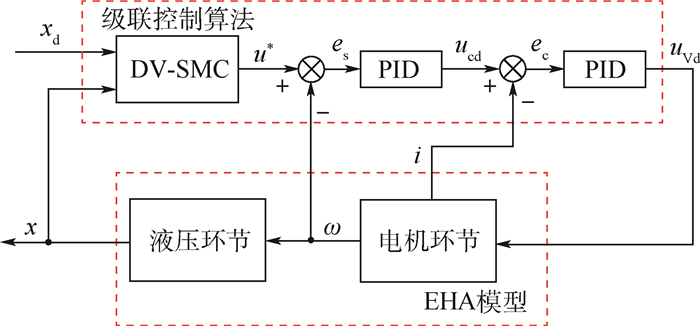
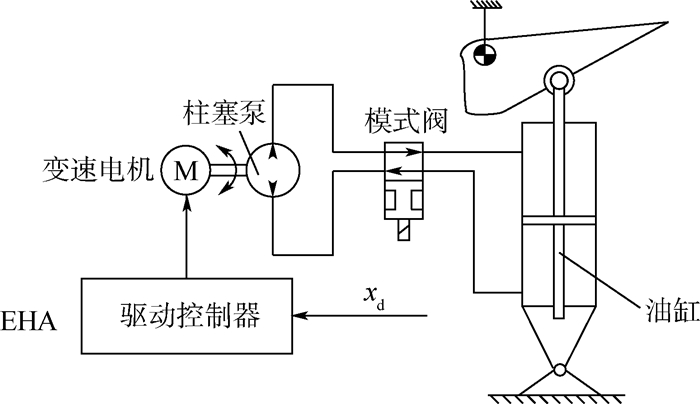
为改善电动静液作动器（EHA）的动态性能，提出了一种基于新型准自适应变阻尼滑模控制（DV-SMC）和PID控制的级联控制（CC）算法。所提算法将高阶EHA分为液压和机械2个低阶系统，分别对2个低阶系统采用了DV-SMC和双环PID控制策略。DV-SMC方法能够自适应调整滑模面阻尼。在起始阶段采用欠阻尼、末段自适应调节为过阻尼，从而在保证EHA快速性的同时也能够完全抑制超调现象。通过仿真验证了所提算法的有效性，并讨论给出了DV-SMC滑模面最优参数。
- 滑模控制(SMC) /
- 准自适应 /
- 变阻尼 /
- 电动静液作动器(EHA) /
- 级联控制(CC)
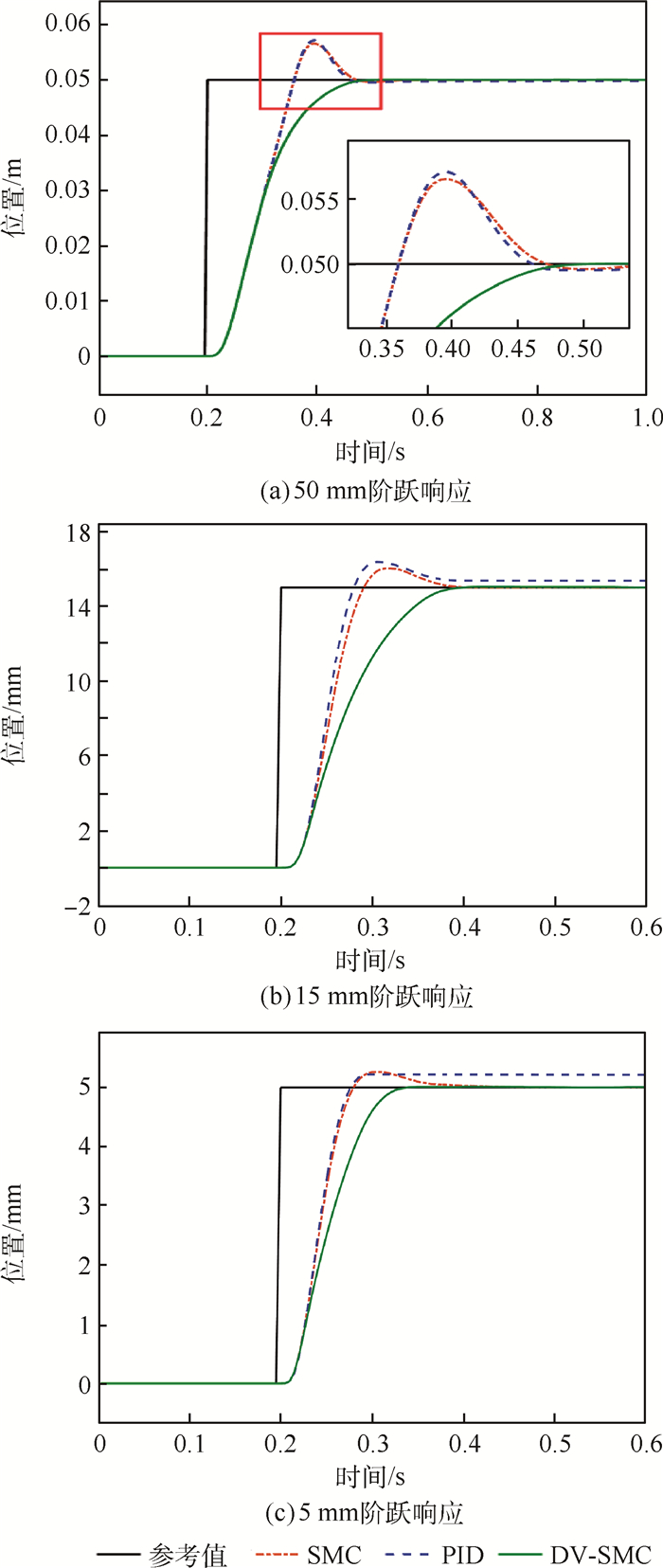
Abstract:
Aimed at improving the performance of an Electro-Hydrostatic Actuator (EHA), a novel Cascade Control (CC) algorithm based on Damping-Variable Sliding Mode Control (DV-SMC) and PID is proposed in this paper. A high-order model of EHA was divided into two low-order subsystems, i.e. mechanical subsystem and hydraulic subsystem. Furthermore, double-loop PID and DV-SMC were applied for the two subsystems, respectively. The proposed method can adjust the damping ratio of the subsystem adaptively. At the beginning of sliding, small damping ratio was used, while an overdamped subsystem was obtained in the end by adaptive adjustment. Therefore, the EHA rapidness and the suppression of overshoot can be guaranteed simultaneously. Finally, simulative validation was carried out to verify the effectiveness of the proposed method, and the optimal parameters of the sliding mode surface are discussed and given.
- Sliding Mode Control (SMC) /
- quasi-adaptive /
- damping variable /
- Electro-Hydrostatic Actuator (EHA) /
- Cascade Control (CC)

HTML全文

图 1 EHA原理图

Figure 1. Schematic diagram of an EHA

下载: 全尺寸图片幻灯片

图 2 阻尼比的影响随敏感因子变化示意图

Figure 2. Schematic diagram of damping ratio influence changing with sensitivity factor

下载: 全尺寸图片幻灯片

图 3 级联控制算法原理框图

Figure 3. Schematic diagram of proposed cascade control algorithm

下载: 全尺寸图片幻灯片

图 4 EHA不同幅值阶跃信号的响应

Figure 4. Response of EHA step signals with different amplitudes

下载: 全尺寸图片幻灯片

图 5 15 mm阶跃EHA控制量输入仿真结果

Figure 5. Simulation results of EHA control input with 15 mm step signal

下载: 全尺寸图片幻灯片

图 6 变阻尼滑模面

Figure 6. Damping-variable sliding mode surface

下载: 全尺寸图片幻灯片

图 7 ξ_max不同取值的阶跃响应

Figure 7. Step response with different values of ξ_max

下载: 全尺寸图片幻灯片

表 1 EHA模型参数

Table 1. Parameters of EHA model

参数	数值
活塞有效面积A/m²	1.134×10^-3
有效行程/m	0.1
油缸内泄系数L_c/(m³·(s·Pa^-1)^-1)	2.5×10^-11
油液弹性模量β_e/(N·m^-2)	6.86×10⁸
容腔有效体积V₀/m³	4×10^-4
油缸黏性摩擦系数B_c/(N·(m·s^-1)^-1)	1 000
油缸及负载质量M/kg	243
柱塞泵排量D_p/(m³·rad^-1)	3.98×10^-7
电机黏性摩擦系数B_m/(N·m·(rad·s^-1)^-1)	6×10^-4
线电阻R/Ω	0.2
线电感L/mH	1.33
柱塞泵和电机转动惯量J_a/(kg·m²)	4×10^-4
电机扭矩系数K_t/(N·m·A^-1)	0.351
反电动势系数K_e/(V·(rad·s^-1)^-1)	0.234
弹性负载系数K_s/(N·m^-1)	8×10⁸
母线电压/VDC	270

下载: 导出CSV

参考文献(18)

[1]	QI H T, FU Y L, QI X Y, et al. Architecture optimization of more electric aircraft actuation system[J]. Chinese Journal of Aeronautics, 2011, 24(4): 506-513. doi: 10.1016/S1000-9361(11)60058-7
[2]	MARE J, FU J. Review on signal-by-wire and power-by-wire actuation for more electric aircraft[J]. Chinese Journal of Aeronautics, 2017, 30(3): 857-870. doi: 10.1016/j.cja.2017.03.013
[3]	ALLE N, HIREMATH S S, MAKARAM S, et al. Review on electro hydrostatic actuator for flight control[J]. International Journal of Fluid Power, 2016, 17(2): 125-145. doi: 10.1080/14399776.2016.1169743
[4]	NAVATHAA A, BELLADA K, HIREMATHA S S, et al. Dynamic analysis of electro hydrostatic actuation system[J]. Procedia Technology, 2016, 25: 1289-1296. doi: 10.1016/j.protcy.2016.08.223
[5]	YAO Z K, YAO J Y, YAO F Y, et al. Model reference adaptive tracking control for hydraulic servo systems with nonlinear neural-networks[J]. ISA Transactions, 2019, 100: 396-404.
[6]	WANG C W, QUAN L, JIAO Z X, et al. Nonlinear adaptive control of hydraulic system with observing and compensating mismatching uncertainties[J]. IEEE Transactions on Control Systems Technology, 2018, 26(3): 927-937. doi: 10.1109/TCST.2017.2699166
[7]	寇荣发. EHA汽车电控主动悬架的模糊控制实验[J]. 西安科技大学学报, 2009, 29(5): 589-594. doi: 10.3969/j.issn.1672-9315.2009.05.017 KOU R F. Test on fuzzy control for vehicle active suspension with EHA[J]. Journal of Xi'an University of Science and Technology, 2009, 29(5): 589-594(in Chinese). doi: 10.3969/j.issn.1672-9315.2009.05.017
[8]	张振, 李海军, 诸德放. EHA反馈线性化最优滑模面双模糊滑模控制[J]. 北京航空航天大学学报, 2016, 42(7): 1398-1405. doi: 10.13700/j.bh.1001-5965.2015.0454 ZHANG Z, LI H J, ZHU D F. Double fuzzy sliding mode control for EHA based on feedback linearization optimal sliding surface[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1398-1405(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0454
[9]	YANG R R, FU Y L, ZHANG L, et al. A novel sliding mode control framework for electrohydrostatic actuator[J]. Mathematical Problems in Engineering, 2018(11): 1-22.
[10]	ALEMU A E, FU Y L. Sliding mode control of electro-hydrostatic actuator based on extended state observer[C]//29th Chinese Control and Decision Conference. Piscataway: IEEE Press, 2017: 758-763.
[11]	WANG S, HABIBI S, BURTON R. Sliding mode control for an electrohydraulic actuator system with discontinuous non-linear friction[J]. Journal of Systems and Control Engineering, 2008, 222(8): 799-815.
[12]	SOON C C, GHAZALI R, JAAFAR H I, et al. Sliding mode controller design with optimized PID sliding surface using particle swarm algorithm[J]. Procedia Computer Science, 2017, 105: 235-239. doi: 10.1016/j.procs.2017.01.216
[13]	张英臣, 祁晓野. 基于PID和滑模控制的电动静液作动器的研究[J]. 机床与液压, 2017, 45(21): 122-126. ZHANG Y C, QI X Y. Study of electro-hydraulic actuator based on PID and sliding mode control[J]. Machine Tool & Hydraulics, 2017, 45(21): 122-126(in Chinese).
[14]	AHN K K, NAM D N C, JIN M L. Adaptive backstepping control of an electrohydarulic actuator[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(3): 987-995. doi: 10.1109/TMECH.2013.2265312
[15]	REN G G, ESFANDIARI M, SONG J C, et al. Position control of an electrohydrostatic actuator with tolerance to internal leakage[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6): 2224-2232. doi: 10.1109/TCST.2016.2517568
[16]	ZHANG H, LIU X T, WANG J M, et al. Robust H_∞ sliding mode control with pole placement for a fluid power electrohydraulic actuator (EHA) system[J]. International Journal of Advanced Manufacturing Technology, 2014, 73: 1095-1104.
[17]	王永宾, 林辉. 基于滑模控制的机载作动器摩擦转矩补偿研究[J]. 中国机械工程, 2010, 21(7): 809-814. WANG Y B, LIN H. Friction compensation of aircraft actuator based on sliding model control[J]. China Mechanical Engineering, 2010, 21(7): 809-814(in Chinese).
[18]	李小虎, 王孙安, 张育林, 等. 基于反馈变结构控制电动静液作动器的研究[J]. 机床与液压, 2008, 36(12): 71-74. LI X H, WANG S A, ZHANG Y L, et al. Study on sliding mode control based on feedback for electro-hydrostatic actuator[J]. Machine Tool & Hydraulics, 2008, 36(12): 71-74(in Chinese).