Unmanned aerial vehicle swarm formation control based on paired interaction mechanism in jackdaws
-
摘要:
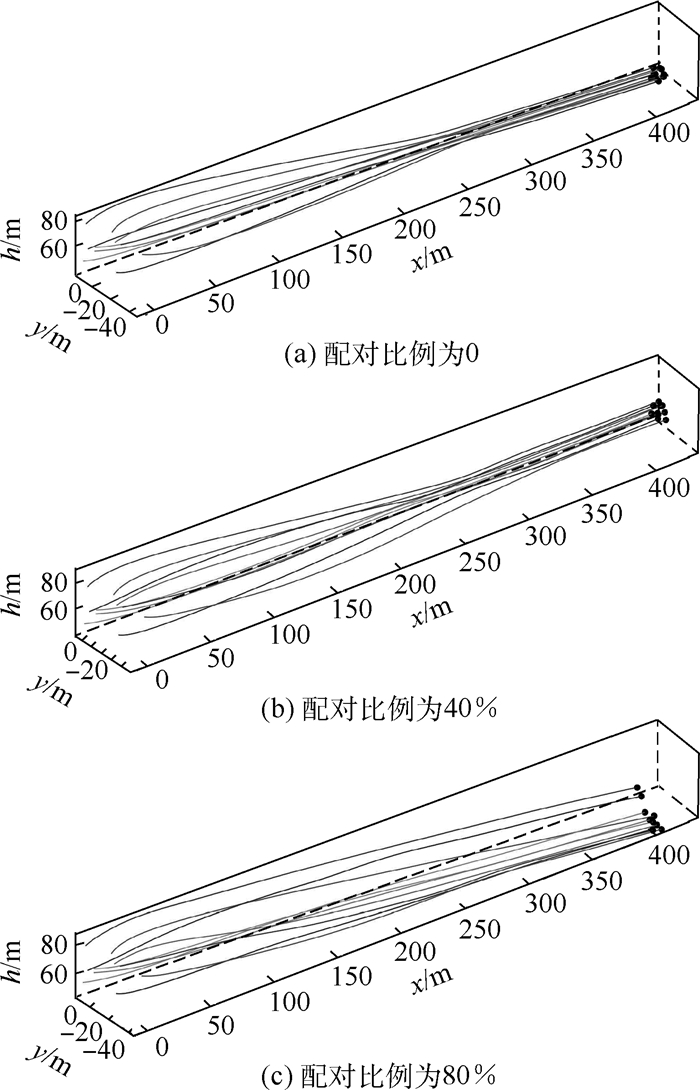
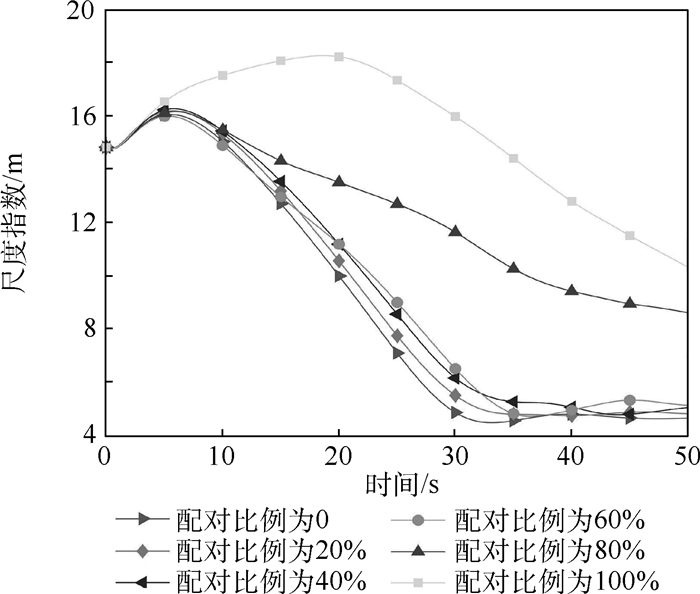
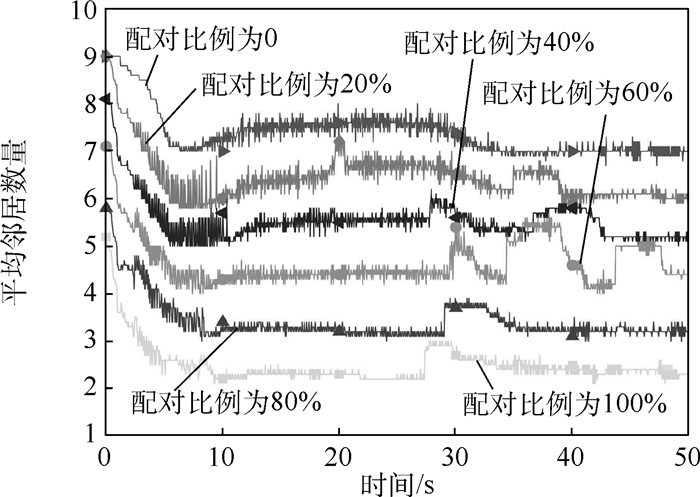
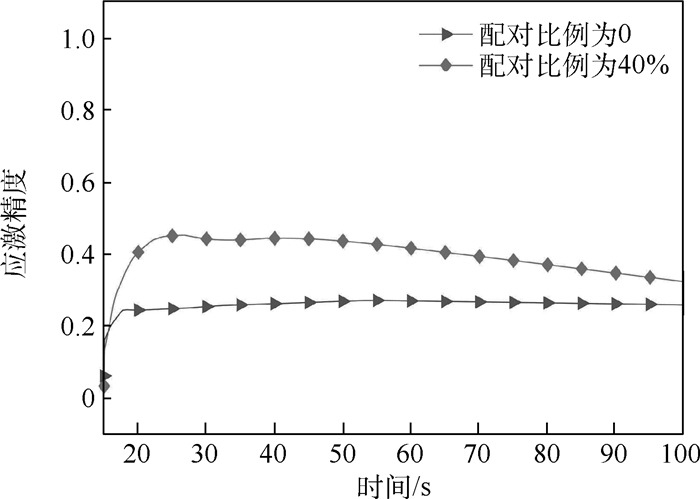
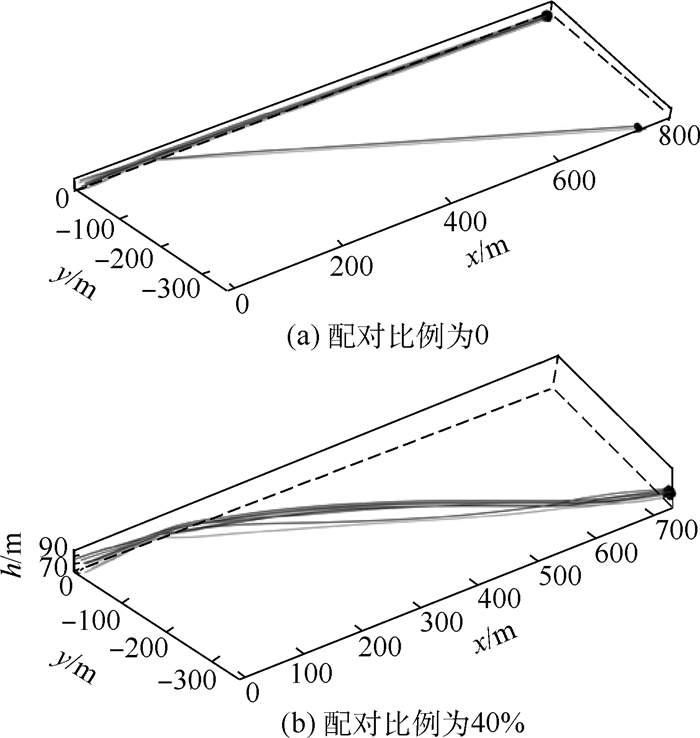
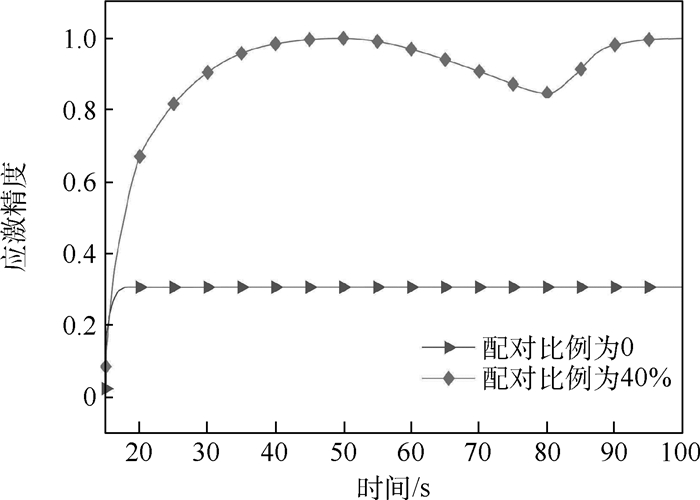
受寒鸦群配对飞行行为机制的启发，提出了一种配对交互模型，并应用于解决无人机（UAV）集群编队控制问题。首先，模仿寒鸦个体间的配对交互，设计配对交互时的邻居选择机制，基于社会力，考虑惯性加速、远距吸引、近距排斥、速度匹配和运动阻尼，分别建立配对个体和未配对个体的运动学微分方程，完成配对交互模型的构建。然后，在无人机模型基础上，设计基于寒鸦配对交互机制的无人机集群编队控制器。最后，通过2组仿真实验研究所提模型应用于无人机集群时的特性。结果表明，寒鸦配对交互模型能保证无人机集群运动的一致性，通过减小无人机交互的平均邻居数量，从而减小无人机集群的通信负载，并且当单向刺激时，配对无人机作为信息无人机时集群有更高的应激精度。
Abstract:Inspired by the paired flight mechanism of jackdaws, a paired interactive swarm model is proposed and applied to the Unmanned Aerial Vehicle (UAV) swarm control system. Firstly, by imitating the paired interaction between jackdaw individuals, the neighbor selection mechanism is designed in pairing interaction. Considering inertial acceleration, long-range attraction, close-range repulsion, speed matching and motion damping, the paired and unpaired individual's differential equation of kinematics is established based on the social forces. Then the construction of the paired interaction model is completed. Secondly, based on the UAV control model, a UAV swarm controller in paired interaction mechanism is designed. Finally, two sets of simulation experiments are conducted to study the characteristics of the model proposed when it is used on the UAV swarm. Simulation results show that the paired interaction model can ensure the consistency of the UAV swarm. The communication load of the UAVs can be reduced by less average number of neighbors in UAV interaction. The UAV swarm has higher stimulation accuracy if the paired UAV is taken as the information individual when facing external stimuli.
-
图 2 极化指数随配对比例变化曲线
Figure 2. Curves of polarization exponent changing with pairing ratio
图 4 平均邻居数量随配对比例变化曲线
Figure 4. Curves of average number of neighbors changing with pairing ratio
图 5 不同配对比例时10%信息无人机占比三维轨迹曲线
Figure 5. 3D trajectory curves changing with pairing ratio with information UAV ratio of 10%
图 6 10%信息无人机占比下应激精度随配对比例变化曲线
Figure 6. Curves of stimulation accuracy changing with pairing ratio with information UAV ratio of 10%
图 7 不同配对比例时20%信息无人机占比三维轨迹曲线
Figure 7. 3D trajectory curves changing with pairing ratio with information UAV ratio of 20%
图 8 20%信息无人机占比下应激精度随配对比例变化曲线
Figure 8. Curves of stimulation accuracy changing with pairing ratio with information UAV ratio of 20%
表 1 集群参数设置
Table 1. Swarm parameter setting
参数 数值 惯性系数kine 2 无人机间期望距离dexp/m 5 感知半径Rsen/m 150 阻尼系数ζ 0.008 衰减系数λ 5 速度协同系数kvel 5 位置协同系数kpos 10 极化指数阈值φflock 0.95 配对对象位置系数kpospair 0.4 配对对象速度系数kvelpair 0.4 初始交互距离R0/m 40 自驾仪控制参数αχ, αv, αḣ, αh 0.75, 3, 0.3, 1 最小航速vmin/(m·s-1) 7.5 最大航速vmax/(m·s-1) 13.5 最大航向角速度ωmax/(rad·s-1) 0.671 
下载: 导出CSV
-
[1] KARIMODDINI A, LIN H, CHEN B M, et al. Hybrid three-dimensional formation control for unmanned helicopters[J]. Automatica, 2013, 49(2): 424-433. doi: 10.1016/j.automatica.2012.10.008 [2] 何吕龙, 张佳强, 侯岳奇, 等. 有向通信拓扑和时延条件下的无人机集群时变编队控制[J]. 北京航空航天大学学报, 2020, 46(2): 314-323. doi: 10.13700/j.bh.1001-5965.2019.0206HE L L, ZHANG J Q, HOU Y Q, et al. Time-varying formation control for UAV swarm with directed interaction topology and communication delay[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(2): 314-323(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0206 [3] 马鸣宇, 董朝阳, 王青, 等. 基于事件驱动的多飞行器编队协同控制[J]. 北京航空航天大学学报, 2017, 43(3): 506-515. doi: 10.13700/j.bh.1001-5965.2016.0222MA M Y, DONG C Y, WANG Q, et al. Event-based cooperative control of multiple flight vehicles formation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 506-515(in Chinese). doi: 10.13700/j.bh.1001-5965.2016.0222 [4] ROSA M R, BALDI S, WANG X, et al. Adaptive hierarchical formation control for uncertain Euler-Lagrange systems using distributed inverse dynamics[J]. European Journal of Control, 2019, 48: 52-65. doi: 10.1016/j.ejcon.2018.11.001 [5] TANNER H G, JADBABAIE A, PAPPAS G J.Stable flocking of mobile agents, Part Ⅰ: Fixed topology[C]//42nd IEEE Conference on Decision and Control.Piscataway: IEEE Press, 2003: 2010-2015. [6] TANNER H G, JADBABAIE A, PAPPAS G J.Stable flocking of mobile agents, Part Ⅱ: Dynamic topology[C]//42nd IEEE Conference on Decision and Control.Piscataway: IEEE Press, 2003: 2016-2021. [7] 毛昱天, 陈杰, 方浩, 等. 连通性保持下的多机器人系统分布式集群控制[J]. 控制理论与应用, 2014, 31(10): 1393-1403.MAO Y T, CHEN J, FANG H, et al. Decentralized flocking of multi-robot systems with connectivity maintenance[J]. Control Theory & Applications, 2014, 31(10): 1393-1403(in Chinese). [8] KELLEY D, OUELLETTE N. Emergent dynamics of laboratory insect swarms[J]. Scientific Reports, 2013, 3: 1073. doi: 10.1038/srep01073 [9] GIARDINA I. Collective behavior in animal groups: Theoretical models and empirical studies[J]. HFSP Journal, 2008, 2(4): 205-219. doi: 10.2976/1.2961038 [10] ZHANG H T, CHEN Z, VICSEK T, et al. Route-dependent switch between hierarchical and egalitarian strategies in pigeon flocks[J]. Scientific Reports, 2014, 4: 1-7. http://pubmedcentralcanada.ca/pmcc/articles/PMC4108945/ [11] COUZIN I D, KRAUSE J, JAMES R, et al. Collective memory and spatial sorting in animal groups[J]. Journal of Theoretical Biology, 2002, 218(1): 1-12. doi: 10.1006/jtbi.2002.3065 [12] VICSEK T, CZIRÓK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 75(6): 1226. doi: 10.1103/PhysRevLett.75.1226 [13] 邱华鑫, 段海滨, 范彦铭. 基于鸽群行为机制的多无人机自主编队[J]. 控制理论与应用, 2015, 32(10): 1298-1304. doi: 10.7641/CTA.2015.50314QIU H X, DUAN H B, FAN Y M. Multiple unmanned aerial vehicle autonomous formation based on the behavior mechanism in pigeon flocks[J]. Control Theory & Applications, 2015, 32(10): 1298-1304(in Chinese). doi: 10.7641/CTA.2015.50314 [14] 邱华鑫, 段海滨, 范彦铭, 等. 鸽群交互模式切换模型及其同步性分析[J]. 智能系统学报, 2020, 15(2): 334-343.QIU H X, DUAN H B, FAN Y M, et al. Pigeon flock interaction pattern switching model and its synchronization analysis[J]. CAAI Transactions on Intelligent Systems, 2020, 15(2): 334-343(in Chinese). [15] BALLERINI M, CABIBBO N, CANDELIER R, et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study[J]. Proceedings of the National Academy of Sciences, 2008, 105(4): 1232-1237. doi: 10.1073/pnas.0711437105 [16] BODE N W F, FRANKS D W, WOOD A J. Limited interactions in flocks: Relating model simulations to empirical data[J]. Journal of the Royal Society Interface, 2011, 8(55): 301-304. doi: 10.1098/rsif.2010.0397 [17] HERBERT-READ J E, PERNA A, MANN R P, et al. Inferring the rules of interaction of shoaling fish[J]. Proceedings of the National Academy of Sciences, 2011, 108(46): 18726-18731. doi: 10.1073/pnas.1109355108 [18] JOLLES J W, BOOGERT N J, SRIDHAR V H, et al. Consistent individual differences drive collective behavior and group functioning of schooling fish[J]. Current Biology, 2017, 27(18): 2862-2868. doi: 10.1016/j.cub.2017.08.004 [19] LING H, MCLVOR G E, VAN DER VAART K, et al. Costs and benefits of social relationships in the collective motion of bird flocks[J]. Nature Ecology & Evolution, 2019, 3(6): 943-948. http://www.ncbi.nlm.nih.gov/pubmed/31061474 [20] LING H, MCLVOR G E, VAN DER VAART K, et al. Local interactions and their group-level consequences in flocking jackdaws[J]. Proceedings of the Royal Society B, 2019, 286(1906): 20190865. doi: 10.1098/rspb.2019.0865 [21] HILDENBRANDT H, CARERE C, HEMELRIJK C K. Self-organized aerial displays of thousands of starlings: A model[J]. Behavioral Ecology, 2010, 21(6): 1349-1359. doi: 10.1093/beheco/arq149 [22] PETTIT B, PERNA A, BIRO D, et al. Interaction rules underlying group decisions in homing pigeons[J]. Journal of the Royal Society Interface, 2013, 10(89): 20130529. doi: 10.1098/rsif.2013.0529 [23] REN W. On constrained nonlinear tracking control of a small fixed-wing UAV[J]. Journal of Intelligent and Robotic Systems, 2007, 48(4): 525-537. doi: 10.1007/s10846-006-9123-8 -
下载:
点击查看大图
计量
- 文章访问数: 1323
- HTML全文浏览量: 85
- PDF下载量: 115
- 被引次数: 0
