MSCSG随机误差测试及误差源分析

耿梦梦; 任元; 樊亚洪; 王丽芬; 于春淼

doi:10.13700/j.bh.1001-5965.2020.0269

MSCSG随机误差测试及误差源分析

doi: 10.13700/j.bh.1001-5965.2020.0269

1.
航天工程大学研究生院, 北京 101416
2.
航天工程大学宇航科学与技术系, 北京 101416
3.
北京控制工程研究所, 北京 100190

基金项目:

国家自然科学基金 51475472

国家自然科学基金 51605489

详细信息

通讯作者:
任元. E-mail: renyuan_823@aliyun.com

中图分类号: V448.2
计量
- 文章访问数: 496
- HTML全文浏览量: 48
- PDF下载量: 110
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-16
- 录用日期: 2020-07-03
- 网络出版日期: 2021-08-20

Random error test and error source analysis of MSCSG

1.
Graduate School, Space Engineering University, Beijing 101416, China
2.
Department of Aerospace Science and Technology, Space Engineering University, Beijing 101416, China
3.
Beijing Institute of Control Engineering, Beijing 100190, China

Funds:

National Natural Science Foundation of China 51475472

National Natural Science Foundation of China 51605489

More Information

Corresponding author: REN Yuan. E-mail: renyuan_823@aliyun.com

摘要

摘要:
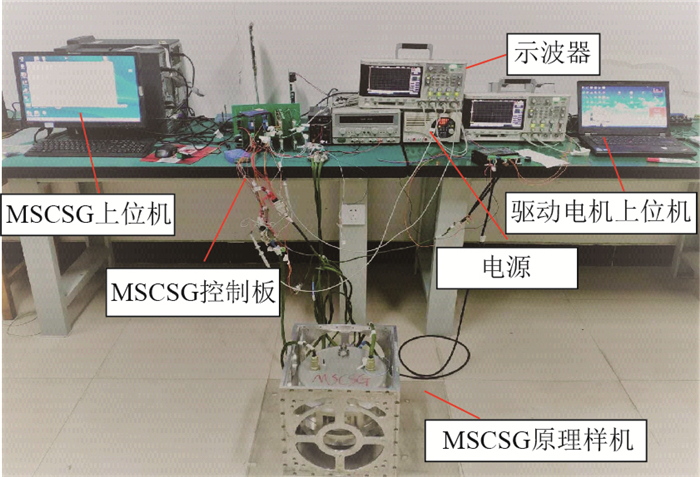
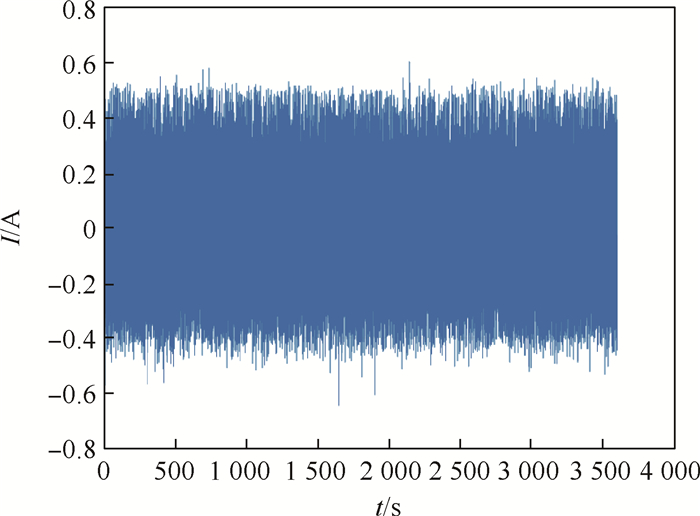
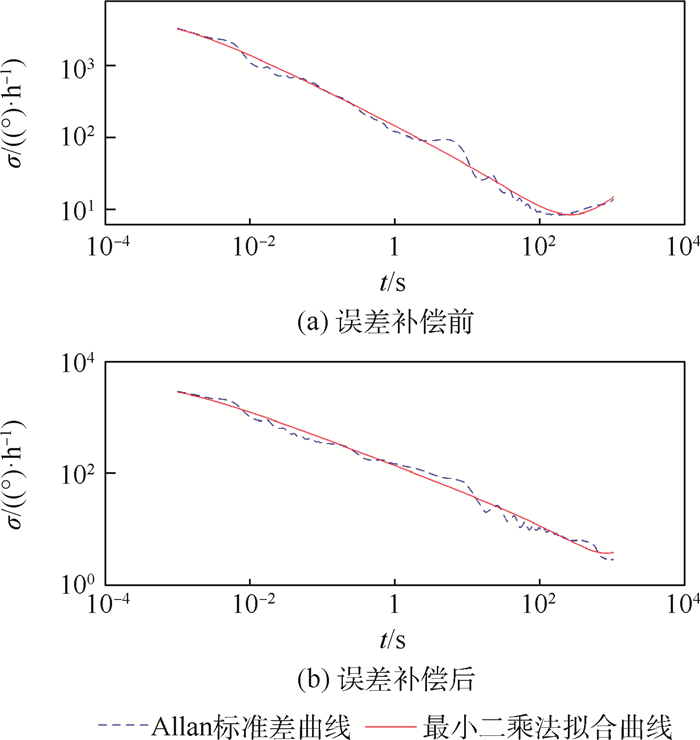
针对磁悬浮控制敏感陀螺(MSCSG)的角速率测量信号中存在较大的随机误差，不利于提高MSCSG敏感精度，以MSCSG原理样机为研究对象，提出采用Allan方差分析法对MSCSG实测数据进行随机误差分析。首先，根据MSCSG角速率敏感原理推导出MSCSG转子偏转角速率的量测公式；其次，应用Allan方差分析法和最小二乘拟合方法计算出5种典型随机误差系数。计算结果显示：在MSCSG随机误差中，零偏不稳定性、速率随机游走以及速率斜坡占主要成分，而量化噪声和角度随机游走误差所占比重较小。依此，对MSCSG误差来源进行了指向性分析，并给出了随机误差的抑制补偿方法，为MSCSG敏感精度的提高奠定了理论基础。
- 磁悬浮控制敏感陀螺(MSCSG) /
- 随机误差 /
- Allan方差分析法 /
- 最小二乘拟合 /
- 误差补偿
Abstract:
There is a large random error in the angular rate measurement signal of Magnetically Suspended Control & Sensing Gyroscope (MSCSG), which is not conducive to improving the sensitivity accuracy of MSCSG. In this paper, taking the principle prototype of MSCSG as the research object, the Allan variance analysis method is proposed to analyze the random error of the measured data of MSCSG. According to the principle of MSCSG angular velocity sensitivity, the measurement formula of MSCSG rotor deflection angular velocity is derived. Five typical random error coefficients are calculated by Allan variance analysis and least square fitting. The calculation results show that, among MSCSG random errors, zero deviation instability, rate following and rate slope are the main components, while quantization noise and angle random walk error account for the smaller proportion. According to this, the directivity of MSCSG error source is analyzed, and the method of restraining and compensating random error is given, which lays a theoretical foundation for improving the sensitivity accuracy of MSCSG.
- Magnetically Suspended Control & Sensing Gyroscope (MSCSG) /
- random error /
- Allan variance analysis method /
- least square fitting /
- error compensation

HTML全文

图 1 MSCSG机械结构图

Figure 1. Mechanical structure of MSCSG

下载: 全尺寸图片幻灯片

图 2 LFMB工作原理图

Figure 2. Schematic diagram of LFMB

下载: 全尺寸图片幻灯片

图 3 MSCSG原理样机的测试实验实物图

Figure 3. Experimental photo of MSCSG prototype

下载: 全尺寸图片幻灯片

图 4 MSCSG采样输出曲线

Figure 4. Sample output curves of MSCSG

下载: 全尺寸图片幻灯片

图 5 MSCSG的Allan标准差双对数及拟合曲线图

Figure 5. Double logarithm of Allan standard deviation and fitting curve of MSCSG

下载: 全尺寸图片幻灯片

图 6 误差补偿前后Allan标准差对比曲线图

Figure 6. Comparison of Allan standard deviation before and after error compensation

下载: 全尺寸图片幻灯片

表 1 Allan标准差与5项典型误差的对应关系

Table 1. Corresponding relations between Allan standard deviation and five typical errors

随机误差项	Allan标准差
量化噪声Q/(°)

零偏不稳定性B/((°)·h^-1)	σ_B=B/0.664 8

速率斜坡R/((°)·h^-2)
注：τ为时间变量。

下载: 导出CSV

表 2 MSCSG各项随机误差统计

Table 2. Statistics of random errors in MSCSG

随机误差项	结果
量化噪声Q/(°)	0.963 036
	2.525 648
零偏不稳定性B/((°)·h^-1)	12.023 988
	32.724 570
速率斜坡R/((°)·h^-2)	38.789 995

下载: 导出CSV

表 3 误差补偿后MSCSG各项随机误差统计

Table 3. Statistics of random errors of MSCSG after error compensation

随机误差项	补偿后结果	误差降低率/%
量化噪声Q/(°)	0.916 159	4.87
	2.365 199	6.35
零偏不稳定性B/((°)·h^-1)	3.235 266	73.09
	10.682 979	36.80
速率斜坡R/((°)·h^-2)	23.970 946	38.20

下载: 导出CSV

参考文献(21)

[1]	任元, 王卫杰, 刘强, 等. 一种磁悬浮控制敏陀螺: 中国, ZL201510006597.5[P]. 2017-04-28. REN Y, WANG W J, LIU Q, et al. A kind of magnetically suspended control sensitive gyroscope: China, ZL201510006597.5[P]. 2017-04-28(in Chinese).
[2]	夏长峰, 蔡远文, 任元, 等. MSCSG转子不平衡振动原理分析与建模[J]. 北京航空航天大学学报, 2018, 44(11): 2321-2328. doi: 10.13700/j.bh.1001-5965.2018.0044 XIA C F, CAI Y W, REN Y, et al. Principle analysis and modeling of rotor imbalance vibration in magnetically suspended control and sensing gyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(11): 2321-2328(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0044
[3]	ZHENG S Q, LI H T, HAN B C, et al. Power consumption reduction for magnetic bearing systems during torque output of control moment gyros[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5752-5759. doi: 10.1109/TPEL.2016.2608660
[4]	HAN B C, ZHENG S Q, LI H T, et al. Weight-reduction design based on integrated radial-axial magnetic bearing of a large-scale MSCMG for space station application[J]. IEEE Transactions on Industrial Electronics, 2016, 64(3): 2205-2214. http://ieeexplore.ieee.org/document/7739998
[5]	LIU X K, ZHAO H, YAO Y, et al. Modeling and analysis of micro-spacecraft attitude sensing with gyrowheel[J]. Sensors, 2016, 16(8): 1321. doi: 10.3390/s16081321
[6]	FANG J C, ZHENG S Q, HAN B C. Attitude sensing and dynamic decoupling based on active magnetic bearing of MSDGCMG[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(2): 338-348. doi: 10.1109/TIM.2011.2164289
[7]	霍元正. MEMS陀螺仪随机漂移误差补偿技术的研究[D]. 南京: 东南大学, 2015: 12-19. HUO Y Z. Research in measurement of MEMS gyroscope random drift compensation[D]. Nanjing: Southeast University, 2015: 12-19(in Chinese).
[8]	熊必凤. 低成本MEMS陀螺仪随机漂移误差的建模及修正[D]. 重庆: 西南大学, 2017: 13-16. XIONG B F. Modeling and correction of random drift error of low cost MEMS gyroscope[D]. Chongqing: Southwest University, 2017: 13-16(in Chinese).
[9]	ALLAN D W, LEVINE J. A historical perspective on the development of the allan variances and their strengths and weaknesses[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(4): 513-519. doi: 10.1109/TUFFC.2016.2524687
[10]	REN Y F, KE X Z, LIU Y J. MEMS gyroscope performance estimate based on allan variance[C]//2007 8th International Conference on Electronic Measurement and Instruments. Piscataway: IEEE Press, 2007: 301-304.
[11]	杜少林, 陈书钊, 陈鹏光, 等. 基于Allan方差的MEMS陀螺仪噪声分析[J]. 仪表技术与传感器, 2018(5): 20-22, 27. https://www.cnki.com.cn/Article/CJFDTOTAL-YBJS201805005.htm DU S L, CHEN S Z, CHEN P G, et al. Analysis of MEMS gyroscope noise based on allan variance[J]. Instrument Technique and Sensor, 2018(5): 20-22, 27(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YBJS201805005.htm
[12]	马群, 王庆, 阳媛, 等. 基于Allan方差的MEMS陀螺仪随机误差辨识与抑制[J]. 传感器与微系统, 2019, 38(6): 62-65. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201906018.htm MA Q, WANG Q, YANG Y, et al. Random error identification and suppression of MEMS gyroscope based on Allan variance[J]. Transducer and Microsystem Technologies, 2019, 38(6): 62-65(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201906018.htm
[13]	贾瑞才. 低成本IMU误差辨识与补偿算法[J]. 四川兵工学报, 2014, 35(5): 97-101. https://www.cnki.com.cn/Article/CJFDTOTAL-CUXI201405028.htm JIA R C. Algorithm of error identification and compensation for low cost IMU[J]. Journal of Sichuan Ordnance, 2014, 35(5): 97-101(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CUXI201405028.htm
[14]	严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2015: 142-143. YAN G M, LI S H, QIN Y Y. Inertial instrument test and data analysis[M]. Beijing: National Defense Industry Press, 2015: 142-143(in Chinese).
[15]	夏长峰, 蔡远文, 任元, 等. MSCSG转子系统的扩展双频Bode图稳定性分析方法[J]. 宇航学报, 2018, 39(2): 168-176. https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201802008.htm XIA C F, CAI Y W, REN Y, et al. Stability analysis method with extended double-frequency bode diagram for rotor of MSCSG[J]. Journal of Astronautics, 2018, 39(2): 168-176(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201802008.htm
[16]	辛朝军, 蔡远文, 任元, 等. 磁悬浮敏感陀螺动力学建模与关键误差源分析[J]. 北京航空航天大学学报, 2016, 42(10): 2048-2058. doi: 10.13700/j.bh.1001-5965.2015.0650 XIN C J, CAI Y W, REN Y, et al. Dynamic modeling and key error sources analysis of magnetically suspended sensitive gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2048-2058(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0650
[17]	YU C M, WANG Z, REN Y, et al. MSCSG two degree of freedom attitude measurement method[C]//Proceedings of the 2nd International Conference on Electrical, Control and Automation(ICECA2018). Beijing: Space Engineering University, 2018: 390-396.
[18]	李磊, 任元, 陈晓岑, 等. 基于ADRC和RBF神经网络的MSCSG控制系统设计[J]. 北京航空航天大学学报, 2020, 46(10): 1966-1972. doi: 10.13700/j.bh.1001-5965.2019.0536 LI L, REN Y, CHEN X C, et al. Design of MSCSG control system based on ADRC and RBF neural network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(10): 1966-1972(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0536
[19]	REN Y, CHEN X C, CAI Y W, et al. Attitude-rate measurement and control integration using magnetically suspended control and sensitive gyroscopes[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4921-4932. http://ieeexplore.ieee.org/document/8106733/
[20]	中国人民解放军战略支援部队航天工程大学. 一种基于磁悬浮控制敏感陀螺平行构型的角运动测量方法: 中国, CN110068336A[P]. 2019-07-30. Space Engineering University, Strategic Support Force of the People's Liberation Army of China. Angular motion measuring method based on parallel configuration of magnetic suspension control sensitive gyroscopes: China, CN110068336A[P]. 2019-07-30(in Chinese).
[21]	辛朝军. 磁悬浮控制敏感陀螺误差分析与补偿方法研究[D]. 北京: 航天工程大学, 2017: 121-162. XIN C J. Compensation method investigation and error analysis for a magnetically suspended control & sensing gyroscope[D]. Beijing: Space Engineering University, 2017: 121-162(in Chinese).