时空约束条件下多旋翼机动轨迹优化方法

蔡志浩; 左一鸣; 王英勋

doi:10.13700/j.bh.1001-5965.2020.0272

时空约束条件下多旋翼机动轨迹优化方法

doi: 10.13700/j.bh.1001-5965.2020.0272

北京航空航天大学自动化科学与电气工程学院, 北京 100083

详细信息

作者简介:
蔡志浩  男, 博士, 高级工程师, 硕士生导师。主要研究方向: 创新布局飞行器系统综合设计、短距/垂直起降无人机建模与控制、无人机自主与协同控制

左一鸣  男, 硕士研究生。主要研究方向: 飞行器的航迹规划

王英勋  男, 硕士, 研究员, 博士生导师。主要研究方向: 无人机自主控制

通讯作者:
蔡志浩. E-mail: caizhihao@outlook.com

中图分类号: V249.122⁺.3
计量
- 文章访问数: 1077
- HTML全文浏览量: 191
- PDF下载量: 80
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-16
- 录用日期: 2020-07-17
- 网络出版日期: 2021-02-20

Maneuver trajectory optimization method of multicopter under space-time constraints

School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China

More Information

Corresponding author: CAI Zhihao. E-mail: caizhihao@outlook.com

摘要

摘要:
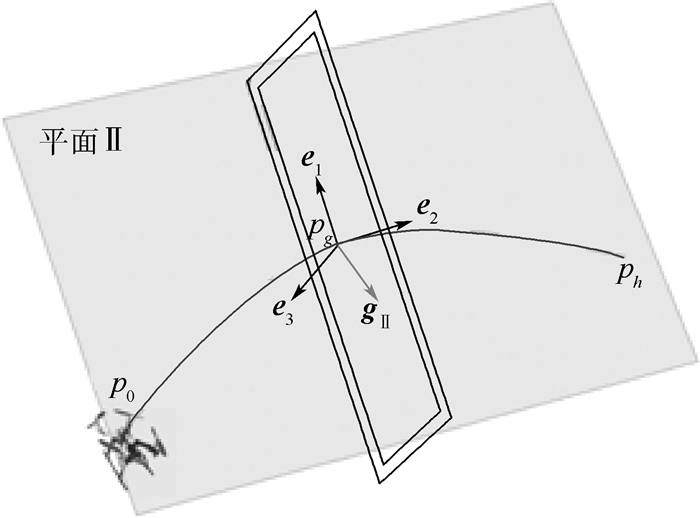
多旋翼飞行器常应用于震后搜救、地质勘探等复杂多变的场景中，考虑到其续航能力及环境特点，优化多旋翼的飞行轨迹以更好更快地完成任务已成为关键问题之一。为此，设定多旋翼穿越室内斜缝的任务场景，提出了一种基于抛物原理和庞特里亚金极小值原理的多约束条件下轨迹优化方法。模仿将东西抛过窄窗的过程，从分析斜缝角度出发，设计一条抛物线轨迹，引导飞行器借助惯性越过斜缝，对于抛掷飞机所需的初始状态，利用庞特里亚金极小值原理设计状态转换轨迹实现。在MATLAB中搭建3D模型验证穿越效果，试验显示，多旋翼最大能穿越竖直方向63°倾斜或水平方向32°倾斜的斜缝。
- 多旋翼 /
- 多约束 /
- 轨迹优化 /
- 抛物原理 /
- 状态转换
Abstract:
Multicopter are often used in complex and variable scenarios such as post-earthquake search and rescue, geological exploration, etc. Considering their endurance and environmental characteristics, optimizing the flight trajectory of multicopter to complete tasks better and faster has become a key issue. To this end, a multicopter's traversing indoor diagonal slit mission is set up, and a trajectory optimization method under multi-constraint based on the parabolic principle and the Pontryagin's minimum principle is proposed. By imitating the process of throwing things through a narrow window and from the perspective of analyzing the oblique slit of the task object, a parabolic trajectory is designed to guide the aircraft to cross the oblique slit with inertia. For the initial state required to throw the aircraft, Pontryagin's minimum principle is usedto realize the state transition trajectory. A 3D model was built in MATLAB to verify the crossing effect. The experiment shows that the multicopter can pass through the inclined seam with a vertical tilt of 63° or a horizontal tilt of 32°.
- multicopter /
- multi-constraint /
- trajectory optimization /
- parabolic principle /
- state transition

HTML全文

图 1 大疆F330

Figure 1. DJI F330

下载: 全尺寸图片幻灯片

图 2 斜缝示意图

Figure 2. Schematic diagram of diagonal seam

下载: 全尺寸图片幻灯片

图 3 平面Ⅱ内飞行轨迹

Figure 3. Flying trajectory in Plane Ⅱ

下载: 全尺寸图片幻灯片

图 4 可行域范围

Figure 4. Feasible range

下载: 全尺寸图片幻灯片

图 5 起飞悬停控制器位置响应

Figure 5. Location response of takeoff hovering controller

下载: 全尺寸图片幻灯片

图 6 回稳控制器响应

Figure 6. Response ofstabilization controller

下载: 全尺寸图片幻灯片

图 7 追踪控制器速度、加速度响应

Figure 7. Track controller speed and acceleration response

下载: 全尺寸图片幻灯片

图 8 任务规划模型

Figure 8. Mission planning model

下载: 全尺寸图片幻灯片

图 9 飞行任务流程

Figure 9. Flight mission process

下载: 全尺寸图片幻灯片

图 10 状态机工作流程

Figure 10. State machine workflow

下载: 全尺寸图片幻灯片

图 11 传感器检测情况

Figure 11. Sensor detection

下载: 全尺寸图片幻灯片

图 12 靠近段轨迹加速度响应

Figure 12. Acceleration response of tracking of approach trajectory

下载: 全尺寸图片幻灯片

图 13 位置与朝向条件变化下穿越结果

Figure 13. Crossing results at different locations and directions

下载: 全尺寸图片幻灯片

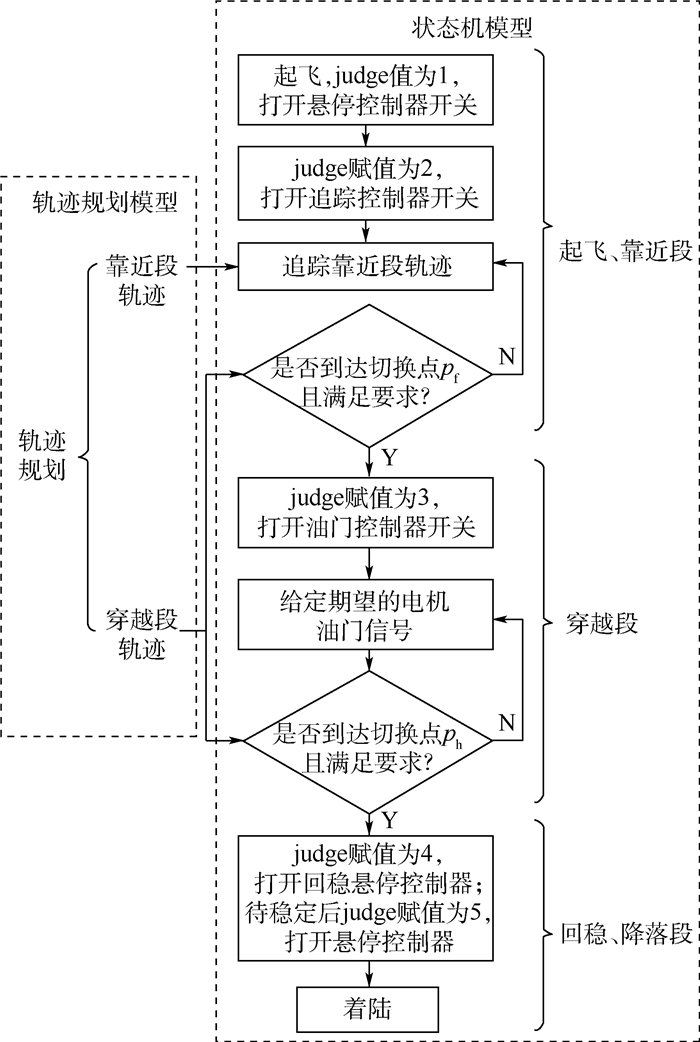
表 1 状态机参数

Table 1. State machine parameters

切换点	位置误差/cm	速度误差/(cm·s^-1)	加速度误差/(cm·s^-2)
穿缝起飞点	1		5
抛出点	2	5	250
回稳点	15
着陆时刻			300

下载: 导出CSV

表 2 四旋翼穿缝性能

Table 2. Sewing ability of quadrotor

斜缝状态	4 m/s	5 m/s
竖直方向倾斜	65°	50°
水平方向倾斜	32°	30°
组合倾斜	60°+10° 45°+15° 24°+30°	50°+10° 30°+20° 5°+30°

下载: 导出CSV

参考文献(15)

[1]	韦意豪. 四旋翼无人机轨迹跟踪与避障控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2018: 6-7. WEI Y H.Trajectory tracking and obstacle avoidanceof quadrotor[D]. Harbin: Harbin Institute of Technology, 2018: 6-7(in Chinese).
[2]	王维平, 刘娟. 无人飞行器航迹规划方法综述[J]. 飞行力学, 2010, 28(2): 6-10. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201002002.htm WANG W P, LIU J. Introduction to unmanned air vehicle route planning methods[J]. Flight Dynamics, 2010, 28(2): 6-10(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201002002.htm
[3]	杜萍, 杨春. 飞行器航迹规划算法综述[J]. 飞行力学, 2005, 23(2): 10-14. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX200502003.htm DU P, YANG C. Introduction of air vehicle path planning algorithms[J]. Flight Dynamics, 2005, 23(2): 10-14(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX200502003.htm
[4]	张广林, 胡小梅, 柴剑飞, 等. 路径规划算法及其应用综述[J]. 现代机械, 2011(5): 85-90. https://www.cnki.com.cn/Article/CJFDTOTAL-XDJX201105031.htm ZHANG G L, HU X M, CHAI J F, et al. Summary of path planning algorithm and its application[J]. Modern Machinery, 2011(5): 85-90(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XDJX201105031.htm
[5]	陈功, 傅瑜, 郭继峰. 飞行器轨迹优化方法综述[J]. 飞行力学, 2011, 29(4): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201104001.htm CHEN G, FU Y, GUO J F. Survey of aircraft trajectory optimization methods[J]. Flight Dynamics, 2011, 29(4): 1-5(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201104001.htm
[6]	MELLINGER D, MICHAEL N, KUMAR V. Trajectory generation and control for precise aggressive maneuvers with quadrotors[J]. The International Journal of Robotics Research, 2012, 31(5): 664-674. doi: 10.1177/0278364911434236
[7]	LIU S K, MOHTA K, ATANASOV N, et al. Search-based mot-ion planning for aggressive flight in SE(3)[J]. IEEE Robotics and Automation Letters, 2018, 3(3): 2439-2446. doi: 10.1109/LRA.2018.2795654
[8]	TORDESILLAS J, LOPEZ B T, EVERETT M, et al.FASTER: Fast and safe trajectory planner for flights in unknown environments[EB/OL]. (2020-01-09)[2020-07-25]. https://arxiv.org/abs/2001.04420.
[9]	曾佳, 申功璋. 一种无人机平滑飞行轨迹规划方法[J]. 系统仿真学报, 2008, 20(S1): 470-473. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ2008S1132.htm ZENG J, SHEN G Z. A method of smooth trajectory planning for UAV[J]. Journal of System Simulation, 2008, 20(S1): 470-473(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ2008S1132.htm
[10]	陈杰, 董伟, 盛鑫军, 等. 基于螺旋样条的旋翼无人机区域轨迹规划[J]. 中国机械工程, 2019, 30(12): 1453-1459. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX201912011.htm CHEN J, DONG W, SHENG X J, et al. Regional trajectory planning of unmanned aerial vehicles based on spiral spline[J]. China Mechanical Engineering, 2019, 30(12): 1453-1459(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX201912011.htm
[11]	孟少华, 向锦武, 罗漳平, 等. 微小型无人直升机避障最优轨迹规划[J]. 北京航空航天大学学报, 2014, 40(2): 246-251. https://bhxb.buaa.edu.cn/CN/Y2014/V40/I2/246 MENG S H, XIANG J W, LUO Z P, et al. Optimal trajectory planning for small-scale unmanned helicopter obstacle avoidance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 246-251(in Chinese). https://bhxb.buaa.edu.cn/CN/Y2014/V40/I2/246
[12]	WANG T, WANG L, LIANG J, et al.Autonomous control and trajectory tracking of quadrotor helicopter[C]//2012 IEEE International Conference on Computer Society and Automation Engineering(CSAE).Piscataway: IEEE Press, 2012: 251-255.
[13]	全权. 多旋翼飞行器设计与控制[M]. 北京: 电子工业出版社, 2018: 73-79. QUAN Q. Introduction to multicopter design and control[M]. Beijing: Publishing House of Electtronics Industry, 2018: 73-79(in Chinese).
[14]	FALANGA D, MUEGGLER E, FAESSLER M, et al.Aggressive quadrotor flight through narrow gaps with on-board sensing and computing using active vision[C]//International Conference on Robotics and Automation (ICRA).Piscataway: IEEE Press, 2017: 5774-5781.
[15]	胡寿松, 王执铨, 胡维礼. 最优控制理论与系统[M]. 3版. 北京: 科学出版社, 2017: 49-76. HU S S, WANG Z Q, HU W L. Optimal control theory and system[M]. 3rd ed. Beijing: Science Press, 2017: 49-76(in Chinese).