基于CGAPIO的航天器编队重构路径规划方法

华冰; 孙胜刚; 吴云华; 陈志明

doi:10.13700/j.bh.1001-5965.2020.0277

基于CGAPIO的航天器编队重构路径规划方法

doi: 10.13700/j.bh.1001-5965.2020.0277

南京航空航天大学航天学院, 南京 210016

基金项目:

国家自然科学基金 61973513

国家自然科学基金 61673208

详细信息

作者简介:
华冰女, 博士, 副研究员, 硕士生导师。主要研究方向: 导航制导与控制

孙胜刚男, 硕士研究生。主要研究方向: 航天器智能编队技术

通讯作者:
华冰. E-mail: huabing@nuaa.edu.cn

中图分类号: TP242.6
计量
- 文章访问数: 925
- HTML全文浏览量: 168
- PDF下载量: 198
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-17
- 录用日期: 2020-07-17
- 网络出版日期: 2021-02-20

Path planning method for spacecraft formation reconfiguration based on CGAPIO

College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Funds:

National Natural Science Foundation of China 61973513

National Natural Science Foundation of China 61673208

More Information

Corresponding author: HUA Bing. E-mail: huabing@nuaa.edu.cn

摘要

摘要:
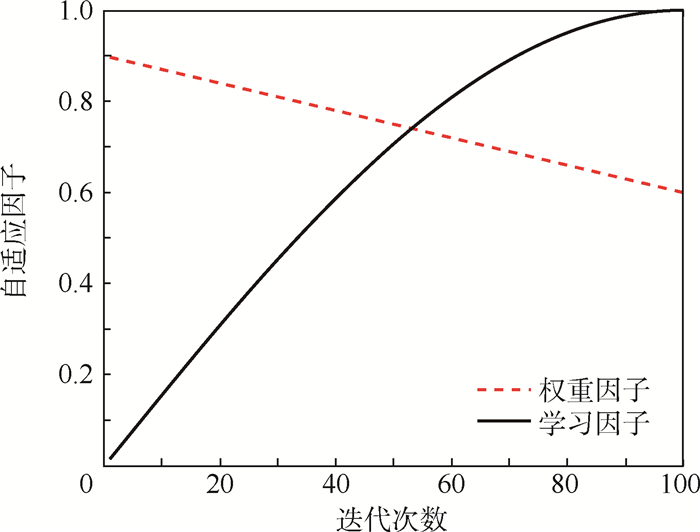
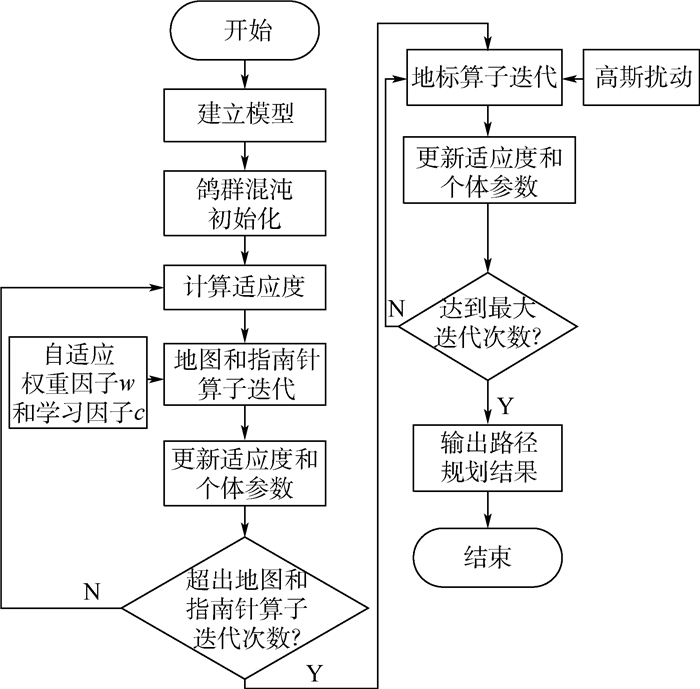
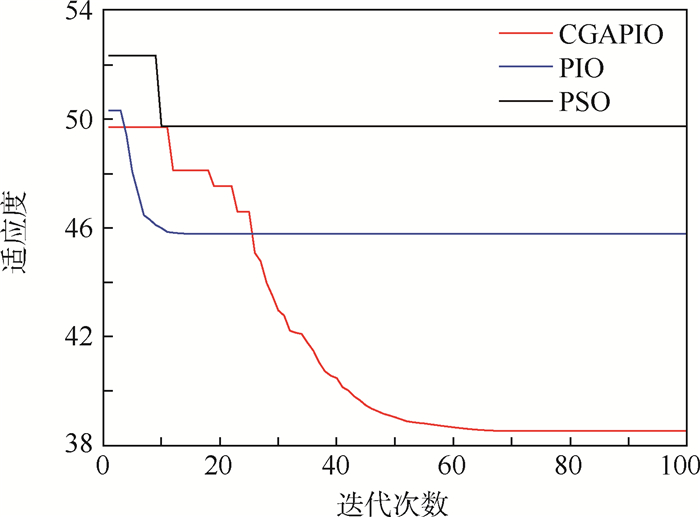
针对航天器编队重构的路径规划问题，考虑燃料消耗和碰撞概率等约束条件，以及基本鸽群算法存在的问题，提出一种基于混沌初始化和高斯扰动的自适应鸽群(CGAPIO)算法。为了得到多样性和覆盖性更好的鸽群初始值，采用Tent Map混沌模型进行鸽群初始化操作；在地图和指南针算子阶段，为提高全局搜索能力，引入了自适应的权重因子和学习因子更新个体的位置和速度；在地标算子阶段，为避免算法陷入局部最优，将高斯扰动加入到鸽群中心位置。仿真实验结果表明：CGAPIO算法与基本鸽群算法和粒子群算法相比，提高了全局搜索能力，避免了局部最优，规划得到的路径更加平滑，各航天器碰撞概率较低，编队重构消耗的总燃料至少减少了12%。
- 航天器编队 /
- 路径规划 /
- 鸽群(PIO)算法 /
- 编队重构 /
- 自适应因子
Abstract:
Aimed at the path planning problem of spacecraft formation reconfiguration, an Adaptive Pigeon-Inspired Optimization algorithm based on Chaos initialization and Gaussian disturbance (CGAPIO)is proposed.In order to make the initial value of the pigeons more diverse and uniform, the Tent Map chaotic model is used to initialize the pigeons. In the map and compass operator, in order to improve the global search ability, adaptive weight factors and learning factors are introduced to update the individual's position and speed; in the landmark operator, in order to avoid the algorithm falling into the local optimum, the Gaussian disturbance is added to the center of the pigeon population.Simulation experiment results show that the CGAPIO significantly improves the global search ability and avoids the local optimum. The planned path is smoother and has lower collision probability of each spacecraft. The total fuel consumed by the formation reconfiguration is significantly reduced by 12% at least compared with the basic pigeon-inspired optimization algorithm and particle swarm optimization algorithm.
- spacecraft formation /
- path planning /
- Pigeon-Inspired Optimization (PIO) algorithm /
- formation reconfiguration /
- adaptive factor

HTML全文

图 1 编队飞行相对参考坐标系

Figure 1. Relative frame of reference for formation flight

下载: 全尺寸图片幻灯片

图 2 不同初始值下的Tent Map混沌模型结果

Figure 2. Results of Tent Map chaotic model with different initial values

下载: 全尺寸图片幻灯片

图 3 随机数与Tent Map混沌模型初始化结果对比

Figure 3. Comparison of initialization results between random numbers and Tent Map chaotic model

下载: 全尺寸图片幻灯片

图 4 自适应权重因子和学习因子随迭代次数的变化

Figure 4. Changes of adaptive weighting factor and learning factor with number of iterations

下载: 全尺寸图片幻灯片

图 5 高斯扰动示意图

Figure 5. Schematic diagram of Gaussian disturbance

下载: 全尺寸图片幻灯片

图 6 CGAPIO算法流程

Figure 6. Flowchart of CGAPIO

下载: 全尺寸图片幻灯片

图 7 CGAPIO算法路径规划结果

Figure 7. Path planning results of CGAPIO

下载: 全尺寸图片幻灯片

图 8 PIO算法路径规划结果

Figure 8. Path planning results of PIO

下载: 全尺寸图片幻灯片

图 9 PSO算法路径规划结果

Figure 9. Path planning results of PSO

下载: 全尺寸图片幻灯片

图 10 不同算法适应度对比

Figure 10. Comparison of fitness curves among different algorithms

下载: 全尺寸图片幻灯片

表 1 航天器初始位置与目标位置

Table 1. Initial and target positions of spacecraft

航天器编号	初始位置/km	目标位置/km
1	(1.732，2，0.034 64)	(0，1，0)
2	(0，4，0)	(0，-2，0)
3	(-1.732，-2，0.034 64)	(0，-1，0)
4	(0，-4，0)	(0，2，0)

下载: 导出CSV

表 2 不同算法总燃料消耗对比

Table 2. Comparison of total fuel consumption among different algorithms

算法	燃料消耗/(km·s^-1)				总燃料消耗/(km·s^-1)
算法	航天器1	航天器2	航天器3	航天器4	总燃料消耗/(km·s^-1)
CGAPIO	0.006 65	0.012 40	0.012 29	0.006 72	0.038 06
PIO	0.007 52	0.015 53	0.015 36	0.007 08	0.045 49
PSO	0.007 04	0.018 16	0.017 19	0.007 14	0.049 53

下载: 导出CSV

参考文献(22)

[1]	李亮, 王洪, 刘良玉, 等. 微小卫星星座与编队技术发展[J]. 空间电子技术, 2017, 14(1): 1-3. https://www.cnki.com.cn/Article/CJFDTOTAL-KJDZ201701001.htm LI L, WANG H, LIU L Y, et al. Microsatellite constellation and formation technology development[J]. Space Electronic Technology, 2017, 14(1): 1-3(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KJDZ201701001.htm
[2]	MAC T T, COPOT C, TRAN D T, et al. Heuristic approaches in robot path planning: A survey[J]. Robotics and Autonomous Systems, 2016, 86: 13-28. doi: 10.1016/j.robot.2016.08.001
[3]	GARCIA M A P, MONTIEL O, CASTILLO O, et al. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation[J]. Applied Soft Computing, 2009, 9(3): 1102-1110. doi: 10.1016/j.asoc.2009.02.014
[4]	DUAN H B, QIAO P X. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning[J]. International Journal of Intelligent Computing and Cybernetics, 2014, 7(1): 24-37. doi: 10.1108/IJICC-02-2014-0005
[5]	林娜, 黄思铭, 拱长青. 基于自适应权重鸽群算法的无人机航路规划[J]. 计算机仿真, 2018, 35(1): 38-42. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201801009.htm LIN N, HUANG S M, GONG C Q. UAV route planning based on adaptive weighted pigeon colony algorithm[J]. Computer Integrated Manufacturing Systems, 2018, 35(1): 38-42(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJZ201801009.htm
[6]	胡耀龙, 冯强, 海星朔, 等. 基于自适应学习策略的改进鸽群优化算法[J/OL]. 北京航空航天大学学报, 2020(2020-02-26)[2020-06-17]. https://doi.org/10.13700/j.bh.1001-5965.2019.0603. HU Y L, FENG Q, HAI X S, et al.Improved pigeon group optimization algorithm based on adaptive learning strategy[J/OL]. Journal of Beijing University of Aeronautics and Astronautics, 2020(2020-02-26)[2020-06-17]. https://doi.org/10.13700/j.bh.1001-5965.2019.0603 (in Chinese).
[7]	崔文豪. J2摄动下的卫星编队队形重构与队形保持方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019: 94-95. CUI W H.Research on satellite formation reconstruction and formation maintenance method under J2 disturbance[D]. Harbin: Harbin Engineering University, 2019: 94-95(in Chinese).
[8]	ZHANG S J, DUAN H B. Gaussian pigeon-inspired optimization approach to orbital spacecraft formation reconfiguration[J]. Chinese Journal of Aeronautics, 2015, 28(1): 200-205. doi: 10.1016/j.cja.2014.12.008
[9]	CLOHESSY W H, WILTSHIRE R S. Terminal guidance system for satellite rendezvous[J]. Journal of the Aerospace Science, 1960, 27(5): 653-658. doi: 10.2514/8.8704
[10]	连淑君, 唐加会, 杜爱华. 带等式约束的光滑优化问题的一类新的精确罚函数[J]. 运筹学学报, 2018, 22(4): 108-116. https://www.cnki.com.cn/Article/CJFDTOTAL-YCXX201804010.htm LIAN S J, TANG J H, DU A H. A new class of exact penalty functions for smooth optimization problems with equality constraints[J]. Operations Research Transactions, 2018, 22(4): 108-116(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YCXX201804010.htm
[11]	崔承刚, 杨晓飞. 基于内部罚函数的进化算法求解约束优化问题[J]. 软件学报, 2015, 26(7): 1688-1699. https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201507011.htm CUI C G, YANG X F. Evolutionary algorithm based on internal penalty function for constrained optimization problems[J]. Journal of Software, 2015, 26(7): 1688-1699(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201507011.htm
[12]	ANTCZAK T. A lower bound for the penalty parameter in the exact minimax penalty function method for solving nondifferentiable extremum problems[J]. Journal of Optimization Theory and Applications, 2013, 159(2): 437-453. doi: 10.1007/s10957-013-0335-3
[13]	HUA B, HUANG Y, WU Y H, et al. Spacecraft formation reconfiguration trajectory planning with avoidance constraints using adaptive pigeon-inspired optimization[J]. Science China Information Sciences, 2019, 62(70209): 1-3.
[14]	聂瑞, 章卫国, 李广文, 等. 基于Tent映射的自适应混沌混合多目标遗传算法[J]. 北京航空航天大学学报, 2012, 38(8): 1010-1016. https://bhxb.buaa.edu.cn/CN/Y2012/V38/I8/1010 NIE R, ZHANG W G, LI G W, et al. Adaptive chaotic hybrid multi-objective genetic algorithm based on Tent mapping[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 1010-1016(in Chinese). https://bhxb.buaa.edu.cn/CN/Y2012/V38/I8/1010
[15]	TAVAZOEI M S, HAERI M. Comparison of different one-dimensional maps as chaotic search pattern in chaos optimization algorithms[J]. Applied Mathematics and Computation, 2007, 187(2): 1076-1085. doi: 10.1016/j.amc.2006.09.087
[16]	段海滨, 叶飞. 鸽群优化算法研究进展[J]. 北京工业大学学报, 2017, 43(1): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201701004.htm DUAN H B, YE F. Research progress of pigeon colony optimization algorithm[J]. Journal of Beijing University of Technology, 2017, 43(1): 1-7(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201701004.htm
[17]	周雨鹏. 基于鸽群算法的函数优化问题求解[D]. 长春: 东北师范大学, 2016: 6-8. ZHOU Y P.Function optimization problem based on pigeon colony algorithm[D]. Changchun: Northeast Normal University, 2016: 6-8(in Chinese).
[18]	陶国娇, 李智. 带认知因子的交叉鸽群算法[J]. 四川大学学报(自然科学版), 2018, 55(2): 295-300. https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX201802014.htm TAO G J, LI Z. Cross-pigeon algorithm with cognitive factors[J]. Journal of Sichuan University(Natural Science Edition), 2018, 55(2): 295-300(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SCDX201802014.htm
[19]	王日宏, 李祥, 李娜. 基于高斯扰动和混沌初始化的狼群算法[J]. 计算机工程与设计, 2019, 40(10): 2879-2884. https://www.cnki.com.cn/Article/CJFDTOTAL-SJSJ201910024.htm WANG R H, LI X, LI N. Wolf pack algorithm based on Gaussian perturbation and chaos initialization[J]. Computer Engineering and Design, 2019, 40(10): 2879-2884(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SJSJ201910024.htm
[20]	王瑞, 肖冰松. 基于改进鸽群优化和马尔可夫链的多无人机协同搜索方法[J]. 工程科学学报, 2019, 41(10): 1342-1350. https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201910014.htm WANG R, XIAO B S. A cooperative search method for multiple UAVs based on improved pigeon optimization and Markov chains[J]. Journal of Engineering Sciences, 2019, 41(10): 1342-1350(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201910014.htm
[21]	艾兵, 董明刚. 基于高斯扰动和自然选择的改进粒子群优化算法[J]. 计算机应用, 2016, 36(3): 687-691. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201603021.htm AI B, DONG M G. Improved particle swarm optimization algorithm based on Gaussian disturbance and natural selection[J]. Journal of Computer Applications, 2016, 36(3): 687-691(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201603021.htm
[22]	朱德刚, 孙辉, 赵嘉, 等. 基于高斯扰动的粒子群优化算法[J]. 计算机应用, 2014, 34(3): 754-759. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201403032.htm ZHU D G, SUN H, ZHAO J, et al. Particle swarm optimization algorithm based on Gaussian perturbation[J]. Journal of Computer Applications, 2014, 34(3): 754-759(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201403032.htm