Optimized Landweber iterative fast image reconstruction algorithm for electromagnetic tomography
-
摘要:
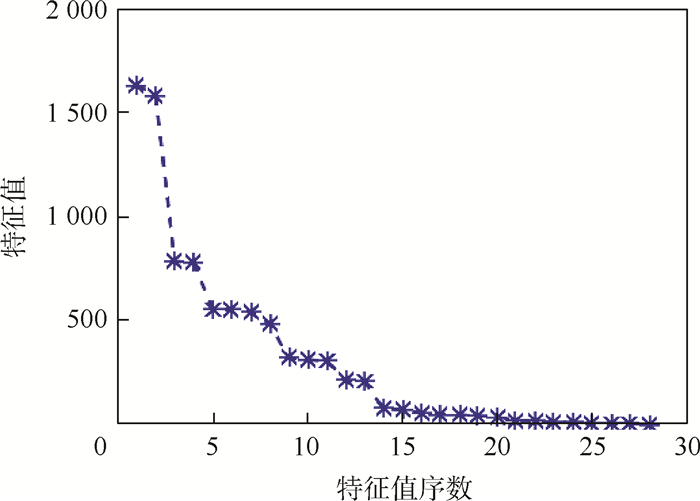
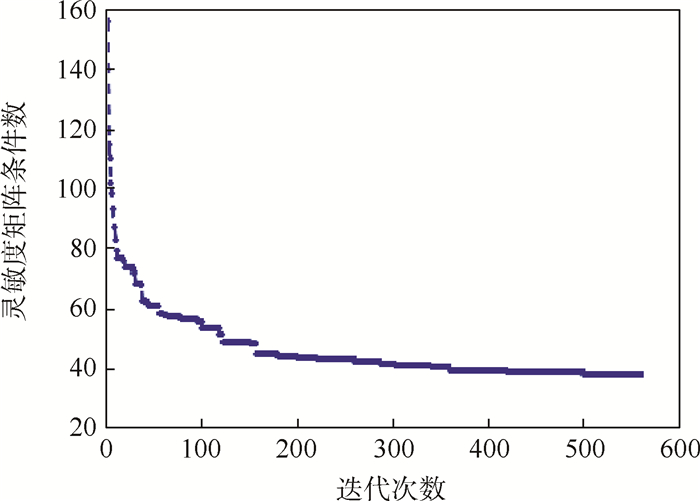
电磁层析成像(EMT)中灵敏度矩阵的病态性、不适定性导致重建图像质量较差。为了提高重建图像的质量与速度，提出了一种优化Landweber迭代快速图像重建算法。首先，对灵敏度矩阵作降维映射，去除灵敏度矩阵中的冗余信息，减少每次迭代的计算量。然后，利用人群搜索算法(SOA)优化降维后的灵敏度矩阵，降低灵敏度矩阵的条件数，改善其病态程度。最后，通过Landweber迭代算法和预处理后的灵敏度矩阵进行图像重建。仿真实验结果表明：相同实验条件下，相比于Landweber迭代算法，所提算法有效提高了成像质量，降低了成像运算量。
-
关键词:
- 电磁层析成像(EMT) /
- 人群搜索算法(SOA) /
- 图像重建 /
- 降维 /
- 灵敏度矩阵优化
Abstract:Due to the pathological property and ill-posedness of sensitivity matrix in Electromagnetic Tomography (EMT), the quality of the reconstructed image is relatively low. To improve the imaging quality and imaging speed, this paper proposes an optimized Landweber iterative fast iteration image reconstruction algorithm. Firstly, dimension reduction algorithm is used to decrease the sensitivity matrix dimension to eliminate the redundant information of sensitivity matrix and reduce the calculation load of each iteration. Secondly, Seeker Optimization Algorithm (SOA) is used to optimize the dimension-reduced sensitivity matrix. This optimization operation can reduce the condition number and improve the morbidity degree of sensitivity matrix. Finally, Landweber iteration algorithm and preprocessed sensitivity matrix are used to reconstruct image. Simulation experimental results show that, under the same experimental conditions, compared with Landweber iteration algorithm, the proposed algorithm increase the quality of reconstructed image and decrease the calculation load of image reconstruction.
-
图 3 灵敏度矩阵条件数收敛曲线
Figure 3. Convergence curve of condition number of sensitivity matrix
表 1 无噪声情况下图像重建结果
Table 1. Results of image reconstruction without noise
表 2 无噪声情况下不同成像算法相关系数比较
Table 2. Comparison of correlation coefficients among different imaging algorithms without noise
模型序号 相关系数 LBP算法 Tikhonov算法 Landweber迭代算法 本文算法 1 0.166 5 0.394 5 0.719 1 0.810 9 2 0.066 1 0.354 5 0.732 8 0.868 9 3 0.112 6 0.385 8 0.719 2 0.754 9 4 0.114 7 0.354 4 0.690 2 0.720 1 5 0.153 1 0.433 1 0.693 2 0.750 7 6 0.075 7 0.146 3 0.435 6 0.794 8 7 0.112 1 0.289 8 0.575 3 0.788 8 8 0.148 2 0.178 1 0.568 1 0.701 8 9 0.239 3 0.279 3 0.539 6 0.642 8 10 0.378 2 0.569 7 0.687 1 0.730 7 
下载: 导出CSV
表 3 无噪声情况下不同成像算法图像误差比较
Table 3. Comparison of image error among different imaging algorithms without noise
模型序号 图像误差 LBP算法 Tikhonov算法 Landweber迭代算法 本文算法 1 1.200 2 1.025 6 0.718 6 0.652 2 2 1.172 5 0.961 8 0.676 1 0.535 1 3 1.195 8 1.034 2 0.792 3 0.756 4 4 1.205 9 1.001 6 0.782 9 0.765 7 5 1.340 6 1.157 3 0.949 7 0.792 5 6 1.071 8 0.974 7 0.894 1 0.608 7 7 1.399 6 0.901 1 0.872 4 0.858 9 8 1.279 4 0.956 3 0.810 4 0.725 2 9 1.589 4 0.907 4 0.850 9 0.862 4 10 0.964 2 0.911 1 0.936 6 0.788 0
下载: 导出CSV
表 4 噪声情况下图像重建结果
Table 4. Results of image reconstruction with noise
表 5 噪声情况下不同成像算法相关系数比较
Table 5. Comparison of correlation coefficients among different imaging algorithms with noise
模型序号 相关系数 LBP算法 Tikhonov算法 Landweber迭代算法 本文算法 1 0.166 8 0.394 2 0.714 3 0.803 1 2 0.066 4 0.351 5 0.728 1 0.862 5 3 0.112 2 0.387 1 0.716 7 0.757 1 4 0.114 1 0.354 7 0.687 2 0.757 1 5 0.152 7 0.433 6 0.695 4 0.756 9 6 0.017 8 0.154 91 0.451 3 0.689 2 7 0.125 9 0.289 2 0.574 3 0.783 3 8 0.141 9 0.176 1 0.565 4 0.691 3 9 0.240 4 0.277 1 0.536 8 0.637 7 10 0.378 0 0.571 3 0.685 1 0.729 4
下载: 导出CSV
表 6 噪声情况下不同成像算法图像误差比较
Table 6. Comparison of image error among different imaging algorithms with noise
模型序号 图像误差 LBP算法 Tikhonov算法 Landweber迭代算法 本文算法 1 1.200 7 1.021 9 0.725 6 0.684 5 2 1.180 3 0.961 9 0.680 8 0.543 2 3 1.191 0 1.033 7 0.763 0 0.804 4 4 1.208 4 0.999 2 0.784 8 0.749 5 5 1.337 8 1.149 5 0.937 7 0.810 4 6 1.006 8 0.974 1 0.886 6 0.712 0 7 1.381 5 0.901 3 0.874 5 0.883 8 8 1.265 1 0.956 8 0.816 5 0.739 9 9 1.597 5 0.908 1 0.850 8 0.874 9 10 0.963 7 0.909 6 0.941 2 0.782 7
下载: 导出CSV
表 7 两种成像算法运算量比较
Table 7. Comparison of calculation load between two imaging algorithms
算法 加法运算量 减法运算量 乘法运算量 本文算法 12 538 644 19 320 Landweber迭代算法 17 682 644 27 048
下载: 导出CSV
-
[1] 李峰, 谭超, 董峰. 全连接深度网络的电学层析成像算法[J]. 工程热物理学报, 2019, 40(7): 1526-1531. https://www.cnki.com.cn/Article/CJFDTOTAL-GCRB201907012.htmLI F, TAN C, DONG F. Fully connected deep network algorithm for electrical tomography[J]. Journal of Engineering Thermophysics, 2019, 40(7): 1526-1531(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCRB201907012.htm [2] 肖理庆, 王化祥. 基于聚类电阻层析成像静态图像重建算法[J]. 仪器仪表学报, 2016, 37(6): 1258-1266. doi: 10.3969/j.issn.0254-3087.2016.06.008XIAO L Q, WANG H X. Absolute image reconstruction algorithm based on clustering for ERT[J]. Chinese Journal of Scientific Instrument, 2016, 37(6): 1258-1266(in Chinese). doi: 10.3969/j.issn.0254-3087.2016.06.008 [3] MA X, PEYTON A J, HIGSON S R, et al. Hardware and software design for an electromagnetic induction tomography (EMT) system for high contrast metal process applications[J]. Measurement Science and Technology, 2006, 17(1): 111-118. doi: 10.1088/0957-0233/17/1/018 [4] WATSON S, WILLIAMS R J, GOUGH W, et al. A magnetic induction tomography system for samples with conductivities below 10 S·m-1[J]. Measurement Science and Technology, 2008, 19(4): 045501. doi: 10.1088/0957-0233/19/4/045501 [5] HUANG A, CAO Z, SUN S, et al. An agile electrical capacitance tomography system with improved frame rates[J]. IEEE Sensors Journal, 2019, 19(4): 1416-1425. doi: 10.1109/JSEN.2018.2880999 [6] SUN S, CAO Z, HUANG A, et al. A high-speed digital electrical capacitance tomography system combining digital recursive demodulation and parallel capacitance measurement[J]. IEEE Sensors Journal, 2017, 17(20): 6690-6698. doi: 10.1109/JSEN.2017.2750741 [7] BROWN B H. Medical impedance tomography and process impedance tomography: A brief review[J]. Measurement Science and Technology, 2008, 19(9): 1-9. http://www.ingentaconnect.com/content/iop/mst/2001/00000012/00000008/art00301 [8] 范文茹, 王勃, 李靓瑶, 等. 基于电阻抗层析成像的CFRP结构损伤检测[J]. 北京航空航天大学学报, 2019, 45(11): 2177-2183. doi: 10.13700/j.bh.1001-5965.2019.0149FAN W R, WANG B, LI J Y, et al. Damage detection of CFRP structure based on electrical impedance tomography[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(11): 2177-2183(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0149 [9] 曾星星, 何敏, 张健, 等. EMT用于金属结构裂纹图像重建的仿真研究[J]. 电子测量与仪器学报, 2020, 34(1): 186-192. https://www.cnki.com.cn/Article/CJFDTOTAL-DZIY202001026.htmZENG X X, HE M, ZHANG J, et al. Simulation study on EMT image reconstruction of metal structure flaw[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(1): 186-192(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DZIY202001026.htm [10] LIU Z, LI W, XUE F, et al. Electromagnetic tomography rail defect inspection[J]. IEEE Transactions on Magnetics, 2015, 51(10): 1-7. http://ieeexplore.ieee.org/document/7102708 [11] 何敏, 柴孟阳. 三种电磁无损检测方法综述[J]. 测控技术, 2012, 31(3): 1-4. doi: 10.3969/j.issn.1000-8829.2012.03.001HE M, CHAI M Y. Summary of three electromagnetic nondestructive testing methods[J]. Measurement & Control Technology, 2012, 31(3): 1-4(in Chinese). doi: 10.3969/j.issn.1000-8829.2012.03.001 [12] 何敏, 刘泽, 董峰, 等. 电磁层析成像技术图像重建的仿真研究[J]. 天津大学学报(自然科学与工程技术版), 2001, 34(4): 435-438. doi: 10.3969/j.issn.0493-2137.2001.04.005HE M, LIU Z, DONG F, et al. Simulation study on image reconstruction of electromagnetic tomography[J]. Journal of Tianjin University (Science and Technology), 2001, 34(4): 435-438(in Chinese). doi: 10.3969/j.issn.0493-2137.2001.04.005 [13] YANG W Q, SPINK D M, YORK T A, et al. An image-reconstruction algorithm based on Landweber's iteration method for electrical-capacitance tomography[J]. Measurement Science and Technology, 1999, 10(11): 1065-1069. doi: 10.1088/0957-0233/10/11/315 [14] 彭黎辉, 陆耿, 杨五强. 电容成像图像重建算法原理及评价[J]. 清华大学学报(自然科学版), 2004, 44(4): 478-484. doi: 10.3321/j.issn:1000-0054.2004.04.013PENG L H, LU G, YANG W Q. Image reconstruction algorithms for electrical capacitance tomography: State of the art[J]. Journal of Tsinghua University (Science and Technology), 2004, 44(4): 478-484(in Chinese). doi: 10.3321/j.issn:1000-0054.2004.04.013 [15] 何元胜, 何敏, 李杰仁. 电磁层析成像图像重建算法[J]. 电气技术, 2007(4): 43-48. doi: 10.3969/j.issn.1673-3800.2007.04.011HE Y S, HE M, LI J R. Review about image reconstruction arithmetic for electromagnetic tomography[J]. Electrical Engineering, 2007(4): 43-48(in Chinese). doi: 10.3969/j.issn.1673-3800.2007.04.011 [16] ROSELL J, CASAÑAS R, SCHARFETTER H. Sensitivity maps and system requirements for magnetic induction tomography using a planar gradiometer[J]. Physiological Measurement, 2001, 22(1): 121-130. doi: 10.1088/0967-3334/22/1/316 [17] 徐凯, 陈广, 尹武良, 等. 基于场量提取法的电磁层析成像系统的灵敏度推算[J]. 传感技术学报, 2011, 24(4): 543-547. doi: 10.3969/j.issn.1004-1699.2011.04.015XU K, CHEN G, YIN W L, et al. Sensitivity derivation and calculation of electromagnetic tomography (EMT) sensor based on field value extraction[J]. Chinese Journal of Sensors and Actuators, 2011, 24(4): 543-547(in Chinese). doi: 10.3969/j.issn.1004-1699.2011.04.015 [18] 刘泽, 肖君, 刘向龙, 等. 一种电磁层析图像快速重建算法[J]. 北京航空航天大学学报, 2018, 44(8): 1569-1576. doi: 10.13700/j.bh.1001-5965.2017.0651LIU Z, XIAO J, LIU X L, et al. An algorithm for fast reconstruction of electromagnetic tomography images[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(8): 1569-1576(in Chinese). doi: 10.13700/j.bh.1001-5965.2017.0651 [19] 张连强, 王东风. 基于改进人群搜索算法的PID参数优化[J]. 计算机工程与设计, 2016, 37(12): 3389-3393. https://www.cnki.com.cn/Article/CJFDTOTAL-SJSJ201612047.htmZHANG L Q, WANG D F. Optimization of PID parameters based on improved seeker optimization[J]. Computer Engineering and Design, 2016, 37(12): 3389-3393(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SJSJ201612047.htm -
下载:
点击查看大图
计量
- 文章访问数: 747
- HTML全文浏览量: 151
- PDF下载量: 89
- 被引次数: 0
