吸气式高超声速飞行器耦合运动数值模拟

丛戎飞; 叶友达; 赵忠良

doi:10.13700/j.bh.1001-5965.2020.0313

吸气式高超声速飞行器耦合运动数值模拟

doi: 10.13700/j.bh.1001-5965.2020.0313

1.
中国空气动力研究与发展中心空天技术研究所, 绵阳 621000
2.
国家计算流体力学实验室, 北京 100083
3.
中国空气动力研究与发展中心高速空气动力研究所, 绵阳 621000

详细信息

通讯作者:
叶友达, E-mail: youdaye@sina.com

中图分类号: V212.1;V221.1⁺5;V221.3
计量
- 文章访问数: 442
- HTML全文浏览量: 38
- PDF下载量: 102
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-03
- 录用日期: 2020-09-09
- 网络出版日期: 2021-09-20

Numerical simulation of coupling motion of an air-breathing hypersonic vehicle

1.
Aerospace Technology Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
2.
National Laboratory for Computational Fluid Dynamics, Beijing 100083, China
3.
High Speed Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China

More Information

Corresponding author: YE Youda, E-mail: youdaye@sina.com

摘要

摘要:
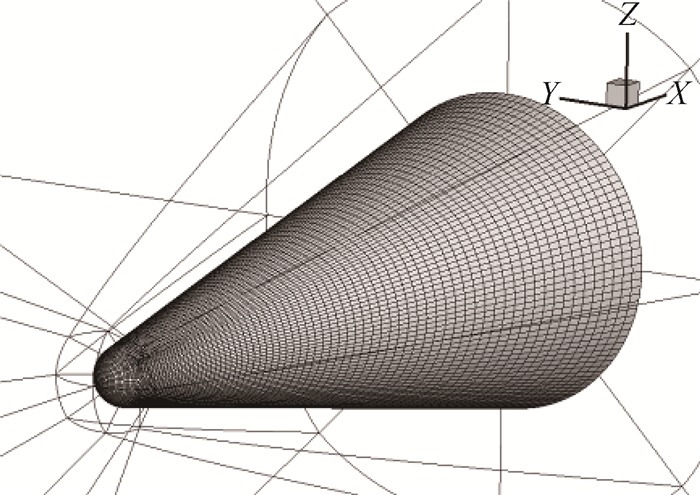
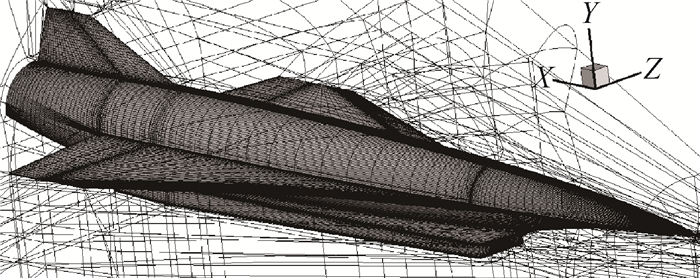
为了研究吸气式高超声速飞行器在俯仰/滚转两自由度耦合运动下的动稳定性问题，基于气动/运动耦合数值模拟方法并结合理论分析，针对一种类似SR-72构型的吸气式高超声速飞行器开展了进气道通流状态下强迫俯仰/自由滚转耦合运动数值模拟研究。结果表明：强迫俯仰/自由滚转耦合运动下，滚转通道的动力学方程可以简化为有阻尼的Mathieu方程形式，并且可以求得稳定性边界。理论分析表明：滚转通道的动稳定性与俯仰振荡角频率相关，在飞行器滚转振荡固有角频率附近存在2个临界角频率，当俯仰振荡角频率位于2个临界角频率之间时，滚转通道是动不稳定的。在俯仰振荡振幅较小时，数值模拟结果与理论符合较好，但实际的临界角频率与理论分析求解的值有一定偏差；数值模拟结果表明随着俯仰振荡振幅增大，导致滚转发散的角频率范围变得更宽，且向更高频率偏移。
- 吸气式高超声速飞行器 /
- 数值模拟 /
- 耦合运动 /
- 动稳定性 /
- Mathieu方程
Abstract:
In order to study the dynamic stability of an air-breathing hypersonic vehicle under coupling motion of pitch/roll, based on the aerodynamic/kinematic coupling numerical simulation method and theoretical analysis, the numerical simulation of forced pitch/free roll coupling motion of an air-breathing hypersonic vehicle with an inlet similar to the SR-72 configuration was carried out. The results show that the dynamic equation of the roll channel under the coupled motion of forced pitch/free roll motion can be simplified to the damped Mathieu equation, and the stability boundary can be obtained. Theoretical analysis shows that the dynamic stability of the roll channel is related to the angular frequency of pitch oscillation. There are two critical angular frequencies around the natural angular frequency of the aircraft roll oscillation. When the angular frequency of pitch oscillation is between the two critical angular frequencies, the roll channel is dynamically unstable. When the pitch amplitude is small, the numerical simulation results are in good agreement with the theory, but there is a certain deviation between the actual critical angle frequency and the theoretical value. The numerical simulation results show that with the increase of pitch amplitude, the angular frequency range resulting in rolling divergence becomes wider and shifts to higher frequencies.
- air-breathing hypersonic vehicle /
- numerical simulation /
- coupling motion /
- dynamic stability /
- Mathieu equation

HTML全文

图 1 模型几何外形及计算网格

Figure 1. Geometric configuration and computational grid of model

下载: 全尺寸图片幻灯片

图 2 模型内流道

Figure 2. Internal flow path of model

下载: 全尺寸图片幻灯片

图 3 钝锥外形及网格拓扑

Figure 3. Blunt cone model configuration and topology of computational grid

下载: 全尺寸图片幻灯片

图 4 气流角位移曲线

Figure 4. Airflow angle displacement curves

下载: 全尺寸图片幻灯片

图 5 滚转力矩系数随滚转角变化曲线

Figure 5. Variation of rolling moment coefficients with rolling angles

下载: 全尺寸图片幻灯片

图 6 滚转静导数随俯仰角变化曲线

Figure 6. Variation of rolling static derivatives with pitch angles

下载: 全尺寸图片幻灯片

图 7 θ=±10°，γ=40°时上下翼面压力云图及物面流线

Figure 7. θ=±10°, γ=40° upper and lower wing surface pressure contours and streamlines

下载: 全尺寸图片幻灯片

图 8 滚转动导数随俯仰角变化曲线

Figure 8. Variation of rolling dynamic derivatives with pitch angles

下载: 全尺寸图片幻灯片

图 9 坐标系定义

Figure 9. Reference frame definition

下载: 全尺寸图片幻灯片

图 10 ω-λ平面图

Figure 10. ω-λ plane graph

下载: 全尺寸图片幻灯片

图 11 不同俯仰振荡频率下俯仰角和滚转角随时间的变化(A=5°)

Figure 11. Time history of pitch angles and rolling angles at different pitch oscillation frequencies(A=5°)

下载: 全尺寸图片幻灯片

图 12 不同俯仰振荡频率下俯仰角和滚转角随时间的变化(A=10°)

Figure 12. Time history of pitch angles and rolling angles at different pitch oscillation frequencies(A=10°)

下载: 全尺寸图片幻灯片

图 13 不同俯仰振荡频率下的滚转相图

Figure 13. Phase diagram of rolling angular velocity to rolling angle at different pitch oscillation frequencies

下载: 全尺寸图片幻灯片

图 14 稳定性平面图

Figure 14. Stability plane graph

下载: 全尺寸图片幻灯片

表 1 数值模拟工况(A=5°)

Table 1. Numerical simulation conditions(A=5°)

编号	f/Hz	ω/(rad·s^-1)	θ₀/(°)
1	0.1	0.628 32	5
2	0.135	0.848 23	5
3	0.15	0.942 48	5
4	0.2	1.256 64	5

下载: 导出CSV

表 2 数值模拟工况(A=10°)

Table 2. Numerical simulation conditions (A=10°)

编号	f/Hz	ω/(rad·s^-1)	θ₀/(°)
1	0.1	0.628 32	5
2	0.15	0.942 48	5
3	0.175	1.099 56	5
4	0.2	1.256 64	5
5	0.25	1.570 8	5

下载: 导出CSV

参考文献(35)

[1]	占云. 超燃冲压发动机的第一个40年[J]. 飞航导弹, 2002(9): 32-40. doi: 10.3969/j.issn.1009-1319.2002.09.012 ZHAN Y. Scramjet's first 40 years[J]. Winged Missiles Journal, 2002(9): 32-40(in Chinese). doi: 10.3969/j.issn.1009-1319.2002.09.012
[2]	王巍巍, 郭琦. 美国典型的高超声速技术研究计划(上)[J]. 燃气涡轮试验与研究, 2013, 26(3): 53-58. doi: 10.3969/j.issn.1672-2620.2013.03.012 WANG W W, GUO Q. Typical hypersonic technology research programs in America (PartⅠ)[J]. Gas Turbine Experiment and Research, 2013, 26(3): 53-58(in Chinese). doi: 10.3969/j.issn.1672-2620.2013.03.012
[3]	PEEBLES C. Road to Mach 10: Lessons learn from the X-43A flight research program[M]. Reston: AIAA, 2008: 36-78.
[4]	SHELLY F, CHARLES M, KENNETH R, et al. Hyper-X Mach 7 scramjet design, ground test and flight result: AIAA-2005-3322[R]. Reston: AIAA, 2005.
[5]	甄华萍, 蒋崇文. 高超声速技术验证飞行器HTV-2综述[J]. 飞航导弹, 2013(6): 7-13. https://www.cnki.com.cn/Article/CJFDTOTAL-FHDD201306005.htm ZHEN H P, JIANG C W. Overview of hypersonic technology verification vehicle HTV-2[J]. Winged Missiles Journal, 2013(6): 7-13(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHDD201306005.htm
[6]	PHILLIPS W H. Effect of rolling on longitudinal and directional stability: NASA TN-1627[R]. Washington, D.C. : NASA, 1948.
[7]	MEHRA R K, CARROLL J V. Bifurcation analysis of aircraft high angle-of-attack flight dynamics: AIAA-1980-1599[R]. Reston: AIAA, 1980.
[8]	KANDIL O A, MENZIES M A. Effective control of simulated wing rock in subsonic flow: AIAA-1997-0831[R]. Reston: AIAA, 1997.
[9]	LIU W, ZHANG H X, ZHAO H Y. Numerical simulation and physical characteristics analysis for slender wing rock[J]. Journal of Aircraft, 2006, 43(3): 858-861. doi: 10.2514/1.18554
[10]	杨小亮, 刘伟, 赵云飞, 等. 80°后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性数值研究[J]. 空气动力学学报, 2011, 29(4): 421-426. doi: 10.3969/j.issn.0258-1825.2011.04.004 YANG X L, LIU W, ZHAO Y F, et al. Numerical investigation of the characteristics of double degree-of-freedom motion of an 80° delta wing in force-pitch and free-roll[J]. Acta Aerodynamica Sinica, 2011, 29(4): 421-426(in Chinese). doi: 10.3969/j.issn.0258-1825.2011.04.004
[11]	陈坚强, 陈琦, 袁先旭, 等. 方形截面飞行器上仰机动对滚转特性影响的数值模拟[J]. 航空学报, 2016, 37(8): 2565-2573. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201608022.htm CHEN J Q, CHEN Q, YUAN X X, et al. Numerical simulation of rolling characteristics in nose-up process of square cross section vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2565-2573(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201608022.htm
[12]	陈琦, 陈坚强, 袁先旭, 等. 方形截面弹俯仰振荡对滚转特性的影响[J]. 力学学报, 2016, 48(6): 1281-1289. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201606002.htm CHEN Q, CHEN J Q, YUAN X X, et al. Numerical study of the effect of forced pitching oscillation on rolling characteristics of vehicle[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1281-1289(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201606002.htm
[13]	TARPLEY C, LEWIS M. Stability derivatives for engine integrated waveriders with viscous and pitch effects[C]//32nd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1994: 1-13.
[14]	TARPLEY C, LEWIS M J. Stability derivatives for a hypersonic caret-wing waverider[J]. Journal of Aircraft, 1995, 32(4): 795-803. doi: 10.2514/3.46793
[15]	RUDD L, PINES D, TARPLEY C. Dynamic stability of mission-oriented hypersonic waveriders[C]//37th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1999: 1-12.
[16]	BAUMANN E, BAHM C, STROVERS B, et al. The X-43A six degree of freedom Monte Carlo analysis[C]//46th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2008: 1-38.
[17]	KENNELL C, NEELY A, O'BYRNE S, et al. Measurement of vehicle stability coefficients in hypersonic wind tunnels[C]//20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. Reston: AIAA, 2015: 1-12.
[18]	YE Y D, ZHAO Z L, TIAN H, et al. The stability analysis of rolling motion of hypersonic vehicles and its validations[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(12): 2194-2204. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&filename=JGXG201412003
[19]	YE Y D, TIAN H, ZHANG X F. The stability of rolling motion of hypersonic vehicles with slender configuration under pitching maneuvering[J]. Science China Physics, Mechanics & Astronomy, 2015, 58(6): 1-9. http://search.cnki.net/down/default.aspx?filename=JGXG201506008&dbcode=CJFD&year=2015&dflag=pdfdown
[20]	李乾, 赵忠良, 叶友达, 等. 一种临近空间飞行器静/动态气动特性研究[J]. 空气动力学学报, 2017, 35(4): 504-509. doi: 10.7638/kqdlxxb-2016.0116 LI Q, ZHAO Z L, YE Y D, et al. Numerical and experimental investigation on aerodynamic characteristics for one typical near space vehicle[J]. Acta Aerodynamica Sinica, 2017, 35(4): 504-509(in Chinese). doi: 10.7638/kqdlxxb-2016.0116
[21]	李乾, 赵忠良, 王晓冰, 等. 一种近空间高超声速飞行器滚转稳定性研究[J]. 航空学报, 2018, 39(3): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201803001.htm LI Q, ZHAO Z L, WANG X B, et al. Rolling stability research of a near space hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(3): 1-8(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201803001.htm
[22]	何垒, 姚跃民, 檀望春, 等. 高超声速飞行器偏离稳定判据研究[J]. 弹箭与制导学报, 2018, 38(4): 69-72. https://www.cnki.com.cn/Article/CJFDTOTAL-DJZD201804017.htm HE L, YAO Y M, TAN W C, at al. The research on departure stability criteria for hypersonic vehicle[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2018, 38(4): 69-72(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DJZD201804017.htm
[23]	刘绪. 高超声速内外流一体化飞行器动态特性研究[D]. 长沙: 国防科学技术大学, 2011: 71-78. LIU X. Investigation of dynamic characteristics of hypersonic airframe/propulsion integrative vehicle[D]. Changsha: National University of Defense Technology, 2011: 71-78(in Chinese).
[24]	刘绪, 刘伟, 周云龙, 等. 吸气式内外流一体化飞行器动导数数值模拟[J]. 空气动力学学报, 2015, 33(2): 147-155. https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201502001.htm LIU X, LIU W, ZHOU Y L, et al. Numerical simulation of dynamic derivatives for air-breathing hypersonic vehicle[J]. Acta Aerodynamica Sinica, 2015, 33(2): 147-155(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201502001.htm
[25]	陈琦, 谢昱飞, 袁先旭, 等. 内外流一体化飞行器动导数数值预测[J]. 计算物理, 2018, 35(5): 563-570. https://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201805008.htm CHEN Q, XIE Y F, YUAN X X, at al. Numerical investigation of dynamic derivative forairframe/propulsion integrative vehicles[J]. Chinese Journal of Computational Physics, 2018, 35(5): 563-570(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201805008.htm
[26]	赵忠良, 杨晓娟, 蒋卫民, 等. 高超声速飞行器通流模拟方法与风洞验证技术[J]. 航空学报, 2014, 35(11): 2932-2938. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201411004.htm ZHAO Z L, YANG X J, JIANG W M, et al. Through-flow simulation method and wind tunnel validation technique for hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2932-2938(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201411004.htm
[27]	CHEN J Z, ZHAO Z L, WANG X B, et al. Research on dynamic derivatives test technique for integrative hypersonic vehicle with internal and external flow in wind tunnel[C]//21st AIAA International Space Planes and Hypersonics Technologies Conference. Reston: AIAA, 2017: 1-7.
[28]	姚源, 陈萱. 美国发SR-72高超声速飞机概念[J]. 中国航天, 2013(12): 39-41. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHT201312017.htm YAO Y, CHEN X. America released the SR-72 hypersonic aircraft concept[J]. Aerospace China, 2013(12): 39-41(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHT201312017.htm
[29]	丛戎飞, 叶友达, 赵忠良. 吸气式高超声速飞行器俯仰/滚转耦合运动特性[J]. 航空学报, 2020, 41(4): 123588. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202004008.htm CONG R F, YE Y D, ZHAO Z L. Characteristics of air-breathing hypersonic vehicle in force-pitch and free-roll coupling motion[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(4): 123588(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202004008.htm
[30]	达兴亚, 陶洋, 赵忠良. 基于预估校正和嵌套网格的虚拟飞行数值模拟[J]. 航空学报, 2012, 33(6): 977-983. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201206003.htm DA X Y, TAO Y, ZHAO Z L. Numerical simulation of virtual flight based on prediction correction coupling method and chimera grid[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 977-983(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201206003.htm
[31]	蒋增辉, 宋威, 陈农. 非旋转钝锥高超声速双平面拍摄风洞自由飞试验[J]. 力学学报, 2015, 47(3): 406-413. doi: 10.7638/kqdlxxb-2013.0065 JIANG Z H, SONG W, CHEN N. Hypersonic wind tunnel free-flight test with biplanar optical system on the non-spinning blunt cone[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(3): 406-413(in Chinese). doi: 10.7638/kqdlxxb-2013.0065
[32]	宋威, 赵小见, 鲁伟, 等. 高超声速边界层转捩对旋转钝锥自由飞运动的影响[J]. 航空学报, 2017, 38(11): 121295. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201711008.htm SONG W, ZHAO X J, LU W, et al. Effect of boundary layer transition on free flight motion of hypersonic spinning blunt cone[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(11): 121295(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201711008.htm
[33]	方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M]. 北京: 北京航空航天大学出版社, 2005: 16-32. FANG Z P, CHEN W C, ZHANG S G. Aircraft flight dynamics[M]. Beijing: Beihang University Press, 2005: 16-32(in Chinese).
[34]	陶明德. 有阻尼Mathieu方程的渐近解[J]. 应用数学和力学, 1992, 13(2): 187-191. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199202010.htm TAO M D. Asymptotic solutions of mathieu equation with damping[J]. Applied Mathematics and Mechanics, 1992, 13(2): 187-191(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199202010.htm
[35]	戎海武, 王向东, 徐伟, 等. Mathieu方程的周期解与稳定性[J]. 佛山科学技术学院学报(自然科学版), 2002, 20(3): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-FSDX200203000.htm RONG H W, WANG X D, XU W, et al. Periodic solution and transition curve of Mathieu equation[J]. Journal of Foshan University(Natural Science Edition), 2002, 20(3): 1-4(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FSDX200203000.htm