基于杂波量测集约束的改进MS-MeMBer滤波器

陆小科; 张志国; 孙进平; 孙伟

doi:10.13700/j.bh.1001-5965.2020.0317

基于杂波量测集约束的改进MS-MeMBer滤波器

doi: 10.13700/j.bh.1001-5965.2020.0317

1.
南京电子技术研究所, 南京 210039
2.
北京航空航天大学电子信息工程学院, 北京 100083

基金项目:

国家自然科学基金 61471019

详细信息

通讯作者:
孙进平, E-mail: sunjinping@buaa.edu.cn

中图分类号: TN953
计量
- 文章访问数: 320
- HTML全文浏览量: 36
- PDF下载量: 56
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-03
- 录用日期: 2020-11-06
- 网络出版日期: 2021-09-20

An improved multi-sensor MeMBer filter based on clutter measurement set constraint

1.
Nanjing Research Institute of Electronics Technology, Nanjing 210039, China
2.
School of Electronic and Information Engineering, Beihang University, Beijing 100083, China

Funds:

National Natural Science Foundation of China 61471019

More Information

Corresponding author: SUN Jinping, E-mail: sunjinping@buaa.edu.cn

摘要

摘要:
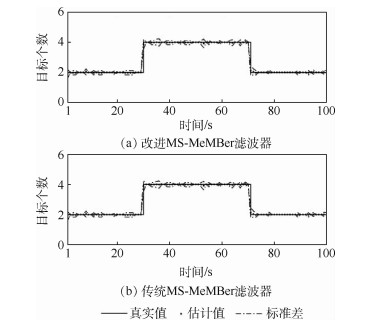
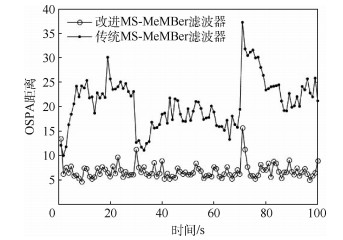
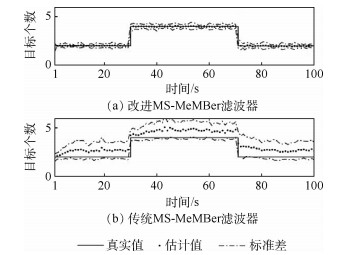
针对高杂波密度场景下，传统多传感器多目标多伯努利(MS-MeMBer)滤波器存在的量测划分假设质量下降、势估计结果出现偏差等问题，提出了一种基于杂波量测集约束的改进MS-MeMBer滤波器。首先，通过将杂波量测集的影响引入到更新过程中，优化了目标量测集的权重，并给出了杂波场景下的单目标多传感器似然函数。然后，通过两步贪婪划分机制，得到了改进的多传感器量测划分假设。通过仿真将所提方法与传统MS-MeMBer滤波器进行了比较，实验结果表明：在高杂波密度场景下，改进MS-MeMBer滤波器具有更优的多目标跟踪性能。
- 多目标跟踪 /
- 多传感器多目标多伯努利(MS-MeMBer)滤波器 /
- 杂波量测集 /
- 量测划分假设 /
- 高杂波密度
Abstract:
To solve the problems existing in the traditional Multi-Sensor Multi-Target Multi-Bernoulli (MS-MeMBer) filter in the high clutter density scene, such as poor quality of measurement partitioning hypothesis and biases of cardinality estimation, an improved MS-MeMBer filter based on clutter measurement set constraint is proposed. By introducing the influence of the clutter measurement set into the update step, the weight of the target measurement set is optimized and the single target multi-sensor likelihood function in the clutter scene is given. After that, the improved multi-sensor measurement partitioning hypothesis is obtained by two-step greedy partition mechanism. The proposed method is compared with the traditional MS-MeMBer filter by simulation. The experimental results show that the proposed method has better multi-target tracking performance in high clutter density scene.
- multi-target tracking /
- Multi-Sensor Multi-Target Multi-Bernoulli (MS-MeMBer) filter /
- clutter measurement set /
- measurement partitioning hypothesis /
- high clutter density

HTML全文

图 1 第1步划分

Figure 1. The first partitioning step

下载: 全尺寸图片幻灯片

图 2 第2步划分

Figure 2. The second partitioning step

下载: 全尺寸图片幻灯片

图 3 目标真实运动轨迹

Figure 3. True movement trajectories of target

下载: 全尺寸图片幻灯片

图 4 OSPA距离比较(λ_k=10)

Figure 4. OSPA distance comparison(λ_k=10)

下载: 全尺寸图片幻灯片

图 5 势估计结果(λ_k=10)

Figure 5. Estimated cardinality(λ_k=10)

下载: 全尺寸图片幻灯片

图 6 OSPA距离比较(λ_k=50)

Figure 6. OSPA distance comparison(λ_k=50)

下载: 全尺寸图片幻灯片

图 7 OSPA距离比较(λ_k=100)

Figure 7. OSPA distance comparison(λ_k=100)

下载: 全尺寸图片幻灯片

图 8 势估计结果(λ_k=50)

Figure 8. Estimated cardinality(λ_k=50)

下载: 全尺寸图片幻灯片

图 9 势估计结果(λ_k=100)

Figure 9. Estimated cardinality(λ_k=100)

下载: 全尺寸图片幻灯片

图 10 平均单步OSPA距离

Figure 10. Average single-step OSPA distance

下载: 全尺寸图片幻灯片

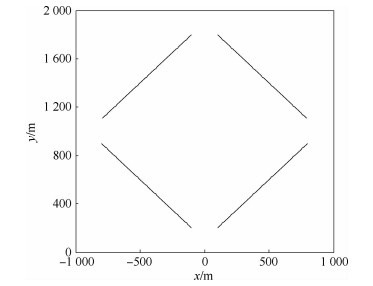
表 1 目标真实运动情况

Table 1. True movement of targets

初始状态	存活时间/s
[-100 m，-10 m/s，1 800 m，-10 m/s]	1~70
[100 m，10 m/s，1 800 m，-10 m/s]	1~70
[-100 m，-10 m/s，200 m，10 m/s]	30~100
[100 m，10 m/s，200 m，10 m/s]	30~100

下载: 导出CSV

表 2 平均单步运行时间

Table 2. Average single-step running time

杂波密度λ_k	平均单步运行时间/ms
杂波密度λ_k	改进MS-MeMBer滤波器	传统MS-MeMBer滤波器
10	23.54	23.22
50	28.85	28.09
100	32.46	33.10

下载: 导出CSV

参考文献(16)

[1]	REID D. An algorithm for tracking multiple targets[J]. IEEE Transactions on Automatic Control, 1979, 24(6): 843-854. doi: 10.1109/TAC.1979.1102177
[2]	KIRUBARAJAN T, BAR-SHALOM Y. Probabilistic data association techniques for target tracking in clutter[J]. Proceedings of the IEEE, 2004, 92(3): 536-557. doi: 10.1109/JPROC.2003.823149
[3]	MAHLER R. Statistical multisource-multitarget information fusion[M]. Norwood: Artech House Press, 2007.
[4]	王颖. 一种鲁棒的多目标概率假设密度算法[J]. 火力与指挥控制, 2018, 43(8): 143-146. doi: 10.3969/j.issn.1002-0640.2018.08.030 WANG Y. A robust multi-target probability hypothesis density algorithm[J]. Fire Control & Command Control, 2018, 43(8): 143-146(in Chinese). doi: 10.3969/j.issn.1002-0640.2018.08.030
[5]	VO B T, VOB N, CANTONI A. Analytic implementations of the cardinalized probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567. doi: 10.1109/TSP.2007.894241
[6]	VO B T, VO B N, CANTONI A. On multi-Bernoulli approximations to the Bayes multi-target filter[C]//Proceeding of the International Conference on Information Fusion, 2007: 1-10.
[7]	陈树新, 洪磊, 吴昊, 等. 学生t混合势均衡多目标多伯努利滤波器[J]. 电子与信息学报, 2019, 41(10): 2457-2463. doi: 10.11999/JEIT181121 CHEN S X, HONG L, WU H, et al. Student's t mixture cardinality balanced multi-target multi-Bernoulli filter[J]. Journal of Electronics & Information Technology, 2019, 41(10): 2457-2463(in Chinese). doi: 10.11999/JEIT181121
[8]	王佰录, 易伟, 李溯琪, 等. 分布式多目标伯努利滤波器的网络共识技术[J]. 信号处理, 2018, 34(1): 1-12. https://www.cnki.com.cn/Article/CJFDTOTAL-XXCN201801001.htm WANG B L, YI W, LI S Q, et al. Consensus for distributed multi-Bernoulli filter[J]. Journal of Signal Processing, 2018, 34(1): 1-12(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XXCN201801001.htm
[9]	彭华甫, 黄高明, 田威. 随机有限集理论及其在多目标跟踪中的应用和实现[J]. 控制与决策, 2019, 34(2): 225-232. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201902001.htm PENG H F, HUANG G M, TIAN W. Random finite set: Theory, application and implementation for multi-target tracking[J]. Control and Decision, 2019, 34(2): 225-232(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201902001.htm
[10]	冯新喜, 迟珞珈, 王泉, 等. 基于箱粒子滤波的混合标签多伯努利跟踪算法[J]. 控制与决策, 2020, 35(2): 507-512. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202002030.htm FENG X X, CHI L J, WANG Q, et al. A hybrid labeled multi-Bernoulli tracking algorithm based on box particle filter[J]. Control and Decision, 2020, 35(2): 507-512(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202002030.htm
[11]	MAHLER R. The multisensor PHD filter: I. General solution via multitarget calculus[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2009, 7336: 73360E-1-73360E-12. doi: 10.1117/12.818024
[12]	MAHLER R. Approximate multisensor CPHD and PHD filters[C]//Proceedings of the International Conference on Information Fusion, 2010: 1-8.
[13]	NANNURU S, BLOUIN S, COATES M, et al. Multisensor CPHD filter[J]. IEEE Transactions on Aerospace and Electronics Systems, 2016, 52(4): 1834-1854. doi: 10.1109/TAES.2016.150265
[14]	SAUCAN A A, COATES M, RABBAT M. A multi-sensor multi-Bernoulli filter[EB/OL]. (2016-09-16)[2020-07-01]. https://arxiv.org/abs/1609.05108.
[15]	SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457. doi: 10.1109/TSP.2008.920469
[16]	RISTIC B, VO B N, CLARK D. Performance evaluation of multi-target tracking using the OSPA metric[C]//Proceedings of the International Conference on Information Fusion, 2010: 1-7.