基于遗传算法的插值Coons曲面孔位修正方法

孙新月; 田威; 胡俊山; 廖文和

doi:10.13700/j.bh.1001-5965.2020.0324

基于遗传算法的插值Coons曲面孔位修正方法

doi: 10.13700/j.bh.1001-5965.2020.0324

南京航空航天大学机电学院, 南京 210016

基金项目:

国家科技重大专项 2018ZX04006001

详细信息

通讯作者:
田威, E-mail: tw_nj@nuaa.edu.cn

中图分类号: V262.4
计量
- 文章访问数: 397
- HTML全文浏览量: 70
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-07
- 录用日期: 2020-08-07
- 网络出版日期: 2021-09-20

A hole position correction method of interpolation Coons surface based on genetic algorithm

College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Funds:

National Science and Technology Major Project of China 2018ZX04006001

More Information

Corresponding author: TIAN Wei, E-mail: tw_nj@nuaa.edu.cn

摘要

摘要:
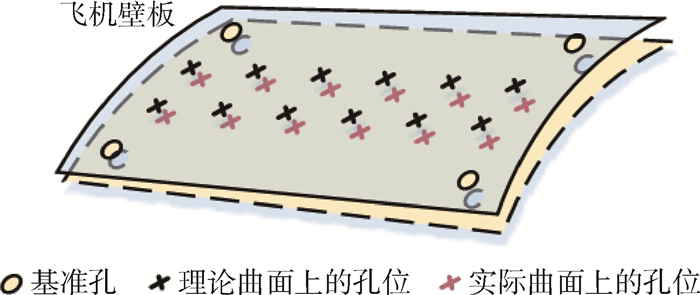
在机器人自动制孔过程中，制孔点位信息通常从待制孔工件工艺数模上获取，而待制孔工件安装过程中会出现位置偏移和变形，由工艺数模得到的点位信息无法直接满足孔位精度要求。为了保证自动制孔的孔位精度，提出了一种基于遗传算法的插值Coons曲面孔位修正方法。利用制孔区域边角基准孔建立双线性Coons误差曲面模型，通过模型计算出待制孔的误差补偿向量，并补偿至理论制孔位置。针对误差曲面切矢模长无法确定的情况，利用制孔区域内的基准孔构建遗传算法模型，计算出切矢模长最优值，使拟合的误差曲面更符合实际制孔区域曲面。通过试验对算法的有效性和精度进行验证，结果表明：采用基于遗传算法的插值Coons曲面孔位修正方法，可以使孔位误差得到有效的补偿。补偿后的平均孔位误差仅为0.195 6 mm，与传统的插值曲面方法相比，孔位误差降低了5%~10%。
- 自动制孔 /
- 位置精度 /
- Coons曲面 /
- 遗传算法 /
- 孔位修正
Abstract:
In the automatic drilling process of the robot, the position of drilling is usually obtained from the process digital model of the workpiece to be drilled, and the position deviation and deformation will occur during the installation process of the workpiece to be drilled. Hence, the hole position accuracy requirement cannot be met if drilling according to the point position obtained from the process digital model directly. This paper proposes an interpolation Coons surface hole position correction method based on genetic algorithm to ensure the hole position accuracy of automatic drilling. The bilinear Coons error surface model is established using the corner reference holes in the drilling area, the error compensation vector of the hole to be drilled is calculated by the model, and the theoretical drilling position is compensated using the error compensation vector. At the same time, the reference holes in the drilling area are used to construct a genetic algorithm model to calculate the optimal value of the tangent vector modulus length to solve the problem that the tangent vector modulus length of the bilinear Coons error surface cannot be determined. The effectiveness and accuracy of the algorithm are verified through experiments. The results show that the use of interpolation Coons surface hole position correction method based on genetic algorithm can effectively compensate the hole position error, and the average hole position error is only 0.195 6 mm after compensation. Compared with the traditional interpolation surface methods, the hole position error is reduced by 5%-10% using interpolation Coons surface hole position correction method based on genetic algorithm.
- automatic drilling /
- position accuracy /
- Coons surface /
- genetic algorithm /
- hole position correction

HTML全文

图 1 理论曲面和实际曲面偏差

Figure 1. Deviation of theoretical surface and actual surface

下载: 全尺寸图片幻灯片

图 2 双线性Coons曲面拟合过程

Figure 2. Process diagram of bilinear Coons surface fitting

下载: 全尺寸图片幻灯片

图 3 单位切矢计算示意图

Figure 3. Schematic diagram of unit tangent vector calculation

下载: 全尺寸图片幻灯片

图 4 切矢模长对曲线丰满程度的影响

Figure 4. Influence of tangent vector length on the fullness of curves

下载: 全尺寸图片幻灯片

图 5 遗传算法求解切矢模长流程

Figure 5. Genetic algorithm for computing the tangent vector modulus length

下载: 全尺寸图片幻灯片

图 6 试验平台

Figure 6. Experimental platform

下载: 全尺寸图片幻灯片

图 7 试验工件孔位分布

Figure 7. Distribution map of hole positions of test pieces

下载: 全尺寸图片幻灯片

图 8 孔位仿真

Figure 8. Hole position simulation

下载: 全尺寸图片幻灯片

图 9 3种孔位修正方法孔位精度对比图

Figure 9. Comparison of hole position accuracy of three hole position correction methods

下载: 全尺寸图片幻灯片

图 10 基准孔位置对孔位误差的影响

Figure 10. Effect of reference hole position on hole position error

下载: 全尺寸图片幻灯片

图 11 基准孔数量对孔位误差的影响

Figure 11. Effect of the number of reference holes on hole position error

下载: 全尺寸图片幻灯片

表 1 边角基准孔理论坐标及法矢

Table 1. Theoretical coordinate and normal vector of corner reference holes

基准孔	(x, y, z) /mm	法矢
A₁	(44.721, 89.443, 20)	(0.447 2, 0.894 4, 0)
B₁	(76.022, 64.967, 20)	(0.760 2, 0.649 7, 0)
C₁	(76.022, 64.967, -20)	(0.760 2, 0.649 7, 0)
D₁	(44.721, 89.443, -20)	(0.447 2, 0.894 4, 0)

下载: 导出CSV

表 2 边角基准孔孔位偏差

Table 2. Position deviation of corner reference holes

基准孔	Δx /mm	Δy /mm	Δz /mm
A₁	-1.702	0.517	-0.049
B₁	-0.691	0.858	-0.203
C₁	-0.624	0.809	-0.402
D₁	-1.82	0.712	-0.161

下载: 导出CSV

表 3 待制孔孔位偏差

Table 3. Position deviation of hole to be drilled

孔号	Δx /mm	Δy /mm	Δz/mm
1	-1.518	0.702	-0.098
2	-1.509	0.694	-0.148
3	-1.65	0.832	-0.259
4	-1.528	0.796	-0.233
5	-1.318	0.754	-0.133
6	-1.207	0.716	-0.134
7	-1.235	0.941	-0.056
8	-1.365	1.021	-0.488
9	-1.276	0.806	-0.282
10	-1.151	0.948	-0.201
11	-0.732	0.674	0.064
12	-0.874	0.793	-0.152
13	-0.87	0.757	-0.08
14	-0.935	0.877	-0.303
15	-0.833	0.871	-0.274

下载: 导出CSV

表 4 孔位修正后的孔位误差对比

Table 4. Comparison of hole position errors after hole position correction

类型	孔位误差范围/mm	平均值/mm
孔位修正前	[0.997, 1.866]	1.476 2
双线性插值法	[0.0314, 0.703]	0.325
插值Coons曲面法	[0.105, 0.608]	0.259 2
基于遗传算法的插值Coons曲面法	[0.058 2, 0.487]	0.195 6

下载: 导出CSV

表 5 仿真数据孔位修正后结果对比

Table 5. Comparison of results after hole position correction of simulation data

类型	孔位误差范围/mm	平均值/mm
孔位修正前	[1.745, 2.655]	2.215
双线性插值法	[0.129, 0.693]	0.324
插值Coons曲面法	[0.205, 0.477]	0.35
基于遗传算法的插值Coons曲面法	[0.132, 0.437]	0.281

下载: 导出CSV

参考文献(17)

[1]	范玉青. 飞机数字化装配技术综述[J]. 航空制造技术, 2006(10): 44-48. https://www.cnki.com.cn/Article/CJFDTOTAL-HKGJ200610008.htm FAN Y Q. Overview of digital assembly technology for aircraft[J]. Aeronautical Manufacturing Technology, 2006(10): 44-48(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKGJ200610008.htm
[2]	LIN C T, WANG M J. Human-robot interaction in an aircraft wing drilling system[J]. International Journal of Industrial Ergonomics, 1999, 23(1-2): 83-94. doi: 10.1016/S0169-8141(97)00103-0
[3]	ZHU W D, MEI B, YAN G R, et al. Measurement error analysis and accuracy enhancement of 2D vision system for robotic drilling[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(2): 160-171. doi: 10.1016/j.rcim.2013.09.014
[4]	袁红璇. 飞机结构件连接孔制造技术[J]. 航空制造技术, 2007(1): 96-99. https://www.cnki.com.cn/Article/CJFDTOTAL-HKGJ200701020.htm YUAN H X. Manufacturing technology of connecting hole in aircraft structures[J]. Aeronautical Manufacturing Technology, 2007(1): 96-99(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKGJ200701020.htm
[5]	何胜强. 大型飞机数字化装配技术与装备[M]. 北京: 航空工业出版社, 2013: 264-272. HE S Q. Digital assembly technologies and equipments of the jumbo aircraft[M]. Beijing: Aviation Industry Press, 2013: 264-272(in Chinese).
[6]	ZHU W D, QU W W, CAO L H, et al. An off-line programming system for robotic drilling in aerospace manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(9-12): 2535-2545. doi: 10.1007/s00170-013-4873-5
[7]	毕运波, 涂国娇, 方伟, 等. 环形轨自动化制孔系统孔位修正方法[J]. 浙江大学学报(工学版), 2015, 49(10): 1863-1869. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201510007.htm BI Y B, TU G J, FANG W, et al. Correcting method of hole position for flexible track automatic drilling system[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(10): 1863-1869(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201510007.htm
[8]	王青, 郑守国, 李江雄, 等. 基于孔边距约束和Shepard插值的孔位修正方法[J]. 航空学报, 2015, 36(12): 4025-4034. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201512026.htm WANG Q, ZHENG S G, LI J X, et al. A correction method for hole positions based on hole margin constraints and Shepard interpolation[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 4025-4034(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201512026.htm
[9]	严秋白. 基于爬行机器人的精准制孔技术研究[D]. 南京: 南京航空航天大学, 2016: 15-20. YAN Q B. Research on precision drilling technology based on crawling robot[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016: 15-20(in Chinese).
[10]	石循磊, 张继文, 刘顺涛, 等. 基于Kriging模型插值的孔位修正策略[J]. 航空学报, 2019, 41(9): 423499. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202009026.htm SHI X L, ZHANG J W, LIU S T, et al. Correction strategy for hole positions based on Kriging interpolation[J]. Acta Aeronautica et Astronautica Sinica, 2019, 41(9): 423499(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202009026.htm
[11]	ZOU C, LIU J H. An off-line programming system for flexible drilling of aircraft wing structures[J]. Assembly Automation, 2011, 31(2): 161-168. doi: 10.1108/01445151111117746
[12]	朱心雄. 自由曲线曲面造型技术[M]. 北京: 科学出版社, 2000: 57-65. ZHU X X. Modeling technology for free curves and surfaces[M]. Beijing: Science Press, 2000: 57-65(in Chinese).
[13]	FERGUSON J. Multivariable curve interpolation[J]. Journal of the ACM, 1964, 11(2): 221-228. doi: 10.1145/321217.321225
[14]	FAUX I D, PRAT M J. Computational geometry for design and manufacture[M]. New York: Ellis Horwood Ltd, 1979: 243.
[15]	CHENG C H, YANG H S. Optimization of geometrical parameters for Stirling engines based on theoretical analysis[J]. Applied Energy, 2012, 92: 395-405.
[16]	郑谐, 王婷, 徐云天. 基于遗传算法的飞机脉动式装配线平衡[J]. 计算机集成制造系统, 2018, 24(6): 1367-1373. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201806005.htm ZHENG X, WANG T, XU Y T. Automatic drilling and riveting technology and its application in digital assembly[J]. Computer Integrated Manufacturing System, 2018, 24(6): 1367-1373(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201806005.htm
[17]	陶杨, 韩维. 基于改进多目标遗传算法的舰尾紊流模拟方法[J]. 北京航空航天大学学报, 2015, 41(3): 443-448. doi: 10.13700/j.bh.1001-5965.2014.0198 TAO Y, HAN W. Carrier airwake simulation methods based on improved multi-objective genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 443-448(in Chinese). doi: 10.13700/j.bh.1001-5965.2014.0198