基于趋势符号聚合近似的卫星时序数据分类方法

阮辉; 刘雷; 胡晓光

doi:10.13700/j.bh.1001-5965.2020.0332

基于趋势符号聚合近似的卫星时序数据分类方法

doi: 10.13700/j.bh.1001-5965.2020.0332

阮辉¹,
刘雷²,
胡晓光^1, ,

1.
北京航空航天大学自动化科学与电气工程学院, 北京 100083
2.
北京机电工程研究所, 北京 100074

基金项目:

国家自然科学基金 51807003

国防基础科研计划 JKCY2016204A102

详细信息

作者简介:
阮辉  男, 博士研究生。主要研究方向: 卫星故障诊断、数据挖掘、数字信号处理

刘雷  男, 硕士, 高级工程师。主要研究方向: 飞行器电气系统

胡晓光  女, 博士, 教授, 博士生导师。主要研究方向: 图像处理、故障诊断、嵌入式测试系统和智能电网

通讯作者:
胡晓光. E-mail: xiaoguang@buaa.edu.cn

中图分类号: V574;TP311
计量
- 文章访问数: 1324
- HTML全文浏览量: 47
- PDF下载量: 80
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-12
- 录用日期: 2020-08-07
- 网络出版日期: 2021-02-20

Satellite time series data classification method based on trend symbolic aggregation approximation

RUAN Hui¹,
LIU Lei²,
HU Xiaoguang^{1
, ,}

1.
School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China
2.
Beijing Electro-Mechanical Engineering Institute, Beijing 100074, China

Funds:

National Natural Science Foundation of China 51807003

National Defense Basic Scientific Research Program of China JKCY2016204A102

More Information

Corresponding author: HU Xiaoguang. E-mail: xiaoguang@buaa.edu.cn

摘要

摘要:
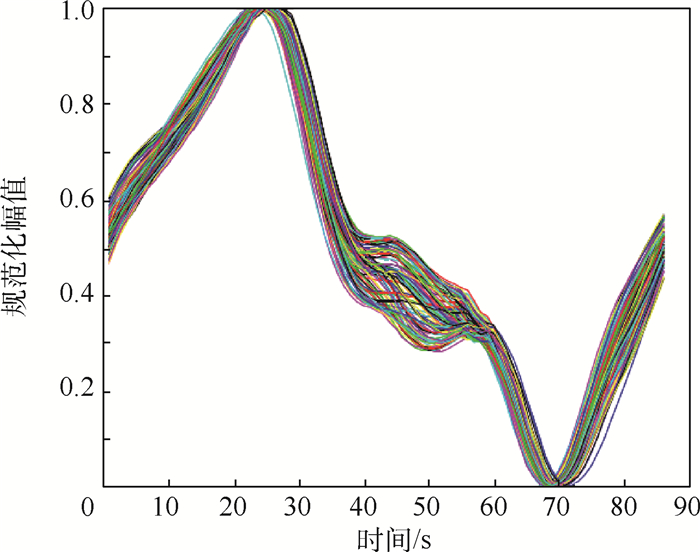
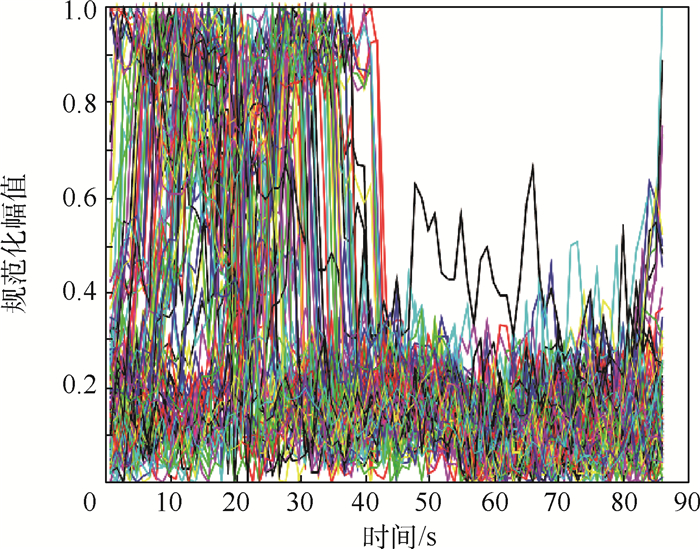
作为在时间序列数据挖掘中广泛使用的主要符号化表示方法，符号聚合近似（SAX）使用段的平均值作为符号表示，由于无法区分具有不同趋势但具有相同平均值符号的不同时间序列，某些情况下可能会导致错误的分类。提出了一种改进的符号表示——趋势符号聚合近似（TrSAX），集成SAX与最小二乘法，用以描述时间序列的均值和斜率，并由此构建出BOTS分类器。此外，对卫星的模拟量遥测时序数据中的角度序列、转速序列、电流序列进行分析，并从UCR公开数据集中筛选出与3种序列类似的3个数据集进行分类实验验证。与应用了SAX和2个改进的SAX、经典的欧氏距离（ED）、动态时间规整（DTW）的1-NN分类方法进行对比，结果表明：提出的BOTS分类方法的分类错误率明显低于其他5种分类方法。
- 卫星遥测数据 /
- 时间序列 /
- 符号化表示 /
- 时间序列 /
- 异常检测
Abstract:
As the main symbolic representation method widely used in time series data mining, the Symbolic Aggregation Approximation (SAX) uses the mean value of segments as the symbolic representation. Since it is impossible to distinguish different time series that have different trends but the same mean value, it may lead to incorrect classification. This paper presents an improved symbol representation-Trend Symbol Aggregation Approximation (TrSAX), which integrates SAX and least squares method to describe the mean and slope value of the time series, and constructs the BOTS classifier. In addition, this paper analyzes the angle sequence, rotation speed sequence, and current sequence in the satellite analog telemetry time series data, and selects three datasets similar to these three sequences from the UCR public dataset for classification experiment verification. They are compared with the 1-NN classification methods using SAX, two improved SAX, classic Euclidean Distance (ED) and Dynamic Time Warping (DTW). The results show that the classification error rate of the proposed BOTS classification method is significantly lower than the other five classification methods.
- satellite telemetry data /
- time series /
- symbolic representation /
- time series classification /
- anomaly detection

HTML全文

图 1 卫星某角度测试时间序列分段叠加结果

Figure 1. Satellite angle test time series segmentation merging results

下载: 全尺寸图片幻灯片

图 2 卫星某转速测试时间序列分段叠加结果

Figure 2. Satellite rotation speed test time series segmentation merging results

下载: 全尺寸图片幻灯片

图 3 卫星某电流测试时间序列分段叠加结果

Figure 3. Satellite electric current test time series segmentation merging results

下载: 全尺寸图片幻灯片

图 4 时间序列划分示意图

Figure 4. Schematic diagram of time series division

下载: 全尺寸图片幻灯片

图 5 φ=3和φ=4时，各平均值和小写字母之间的对应关系

Figure 5. Corresponding relationship between average values and lower-case letters for φ=3 and φ=4

下载: 全尺寸图片幻灯片

图 6 角度间隔和字母的对映关系

Figure 6. Angle interval and corresponding letters

下载: 全尺寸图片幻灯片

图 7 趋势符号聚合近似(TrSAX)表示示意图

Figure 7. Schematic diagram of trend symbolic aggregate approximation (TrSAX) representation

下载: 全尺寸图片幻灯片

图 8 三个数据集的分类错误率结果

Figure 8. Classification Error rate results for three datasets

下载: 全尺寸图片幻灯片

图 9 三个数据集的运行时间结果

Figure 9. Running time results for three datasets

下载: 全尺寸图片幻灯片

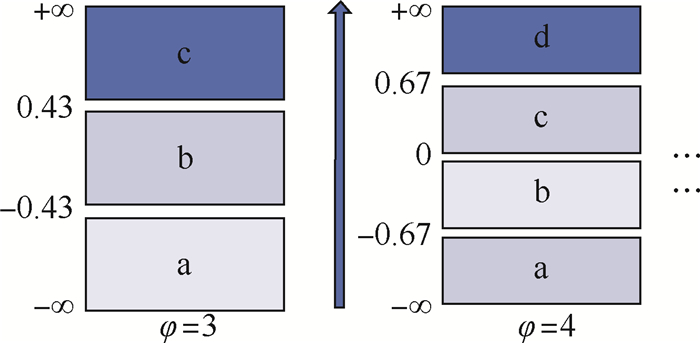
表 1 字母数为3~9的断点查找表

Table 1. Look up table from breakpoints with alphabet sizes from 3 to 5

β_i	3	4	5
β₁	-0.43	-0.67	-0.84
β₂	0.43	0	-0.25
β₃		0.67	0.25
β₄			0.84

下载: 导出CSV

表 2 时间序列的BOTS表示形式的虚拟示例

Table 2. Visual example of BOTS representation for time series

时间序列号	AaAaAa	AaAaAb	…	EaEaEa	…	EdEdEd
1	2	2	…	13	…	0
2	3	1	…	0	…	0
3	1	2	…	12	…	0
⋮	⋮	⋮		⋮	⋮	⋮
m	2	2	…	14	…	0

下载: 导出CSV

表 3 时间序列数据集详细信息

Table 3. Details on time series datasets

数据集编号	名称	训练集/测试集	类别数	序列长度
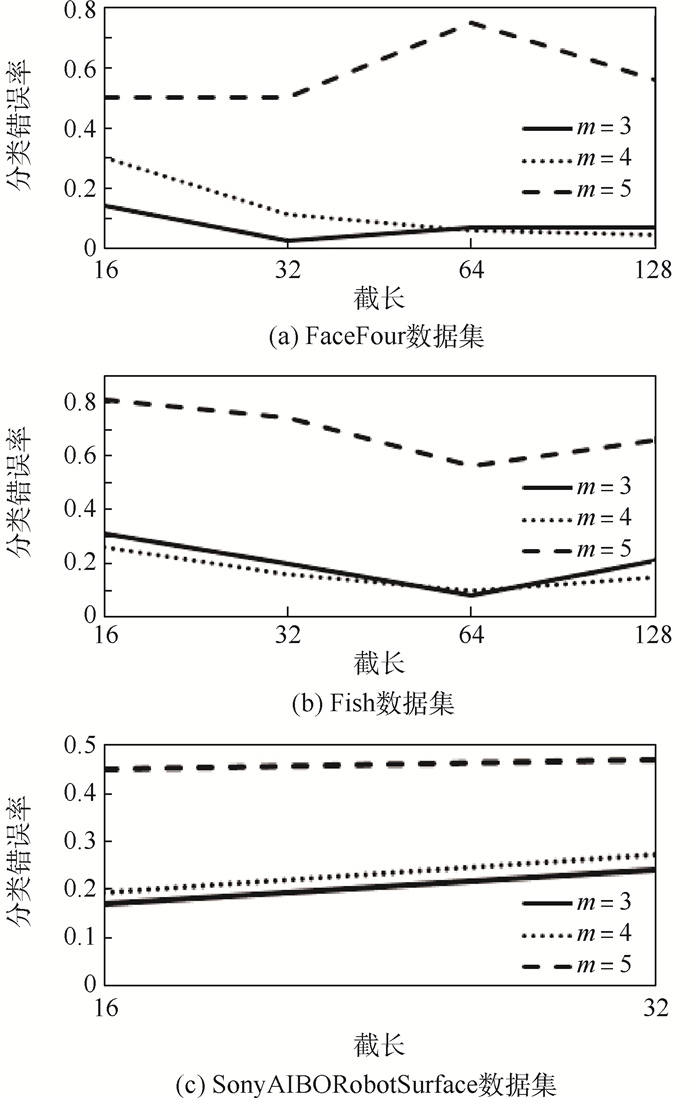
1	SonyAIBO RobotSurface	20/601	2	70
2	Fish	175/175	7	115
3	FaceFour	24/88	4	116

下载: 导出CSV

表 4 不同表示算法的分类结果

Table 4. Classification results of different representation algorithms

数据集	1-NN ED	1-NN DTW	1-NN SAX	1-NN ESAX	1-NN TSAX	BOTS
SongAIBO Robot	0.215	0.199	0.236	0.217	0.187	0.171
Fish	0.198	0.237	0.109	0.469	0.192	0.080
FaceFour	0.222	0.151	0.053	0.182	0.06	0.023
平均秩	4.67	4	3.33	5.33	2.67	1

下载: 导出CSV

参考文献(21)

[1]	杨海民, 潘志松, 白玮. 时间序列预测方法综述[J]. 计算机科学, 2019, 46(1): 21-28. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201901005.htm YANG H M, PAN Z S, BAI W. Review of time series prediction methods[J]. Computer Science, 2019, 46(1): 21-28(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201901005.htm
[2]	史欣田, 庞景月, 张新, 等. 基于集成极限学习机的卫星大数据分析[J]. 仪器仪表学报, 2018, 39(12): 81-91. https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201812010.htm SHI X T, PANG J Y, ZHANG X, et al. Satellite big data analysis based on bagging extreme learning machine[J]. Chinese Journal of Scientific Instrument, 2018, 39(12): 81-91(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201812010.htm
[3]	彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述[J]. 仪器仪表学报, 2016, 37(9): 1929-1945. https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201609003.htm PENG X Y, PANG J Y, PENG Y, et al. Review on anomaly detection of spacecraft telemetry data[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1929-1945(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201609003.htm
[4]	YANG T, CHEN B, GAO Y, et al. Data mining-based fault detection and prediction methods for in-orbit satellite[C]//IEEE International Conference on Measurement, Information and Control.Piscataway: IEEE Press, 2013: 805-808.
[5]	肇刚, 李言俊. 基于时间序列数据挖掘的航天器故障诊断方法[J]. 飞行器测控学报, 2010, 29(3): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-FXCK201003002.htm ZHAO G, LI Y J. Spacecraft fault diagnosis method based on time series data mining[J]. Journal of Spacecraft TT & C Technology, 2010, 29(3): 1-5(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FXCK201003002.htm
[6]	鲍军鹏, 杨科, 周静. 卫星时序数据挖掘节点级并行与优化方法[J]. 北京航空航天大学学报, 2018, 44(12): 2470-2478. doi: 10.13700/j.bh.1001-5965.2018.0334 BAO J P, YANG K, ZHOU J. Node level parallel and optimization method of satellite time serial data mining[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(12): 2470-2478(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0334
[7]	张弓, 翟君武, 杨海峰. 导航卫星遥测数据趋势预测技术研究[J]. 航天器工程, 2017, 3(3): 74-81. https://www.cnki.com.cn/Article/CJFDTOTAL-HTGC201703015.htm ZHANG G, ZHAI J W, YANG H F. Research on telemetry data tendency prognosis for navigation satellite[J]. Spacecraft Engineering, 2017, 3(3): 74-81(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HTGC201703015.htm
[8]	WAN Y, SI Y W. A hidden semi-Markov model for chart pattern matching in financial time series[J]. Soft Computing, 2017, 22(3): 1-20. doi: 10.1007/s00500-017-2703-7
[9]	MUEEN A, KEOGH E, YOUNG N E.Logical-Shapelets: An expressive primitive for time series classification[C]//ACM Sigkdd International Conference on Knowledge Discovery & Data Mining.New York: ACM, 2011: 1154-1162.
[10]	GAO Z K, CAI Q, YANG Y X, et al. Multiscale limited penetrable horizontal visibility graph for analyzing nonlinear time series[J]. Scientific Reports, 2016, 6(1): 35622. doi: 10.1038/srep35622
[11]	XI X, KEOGH E, SHELTON C, et al.Fast time series classification using numerosity reduction[C]//International Conference On Machine Learning, 2006: 1033-1040.
[12]	SAKOE H, CHIBA S. Dynamic programming algorithm optimization for spoken word recognition[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1978, 26(1): 43-49. doi: 10.1109/TASSP.1978.1163055
[13]	RAKESH A, CHRISTOS F, ARUN S.Efficient similarity search in sequence databases[C]//Foundations of Data Organization and Algorithms.Berlin: Springer, 1993: 69-84.
[14]	CHEN Q, CHEN L, LIAN X, et al.Indexable PLA for efficient similarity search[C]//VLDB Endowment in Proceedings of the 33rd International Conference on Very Large Data Bases.2007: 435-446.
[15]	LIN J, KEOGH E, LI W, et al. Experiencing SAX: A novel symbolic representation of time series[J]. Data Mining & Knowledge Discovery, 2007, 15(2): 107-144. http://nar.oxfordjournals.org/external-ref?access_num=10.1007/s10618-007-0064-z&link_type=DOI
[16]	KEOGH E, CHAKRABARTI K, PAZZANI M, et al. Dimensionality reduction for fast similarity search in large time series databases[J]. Knowledge & Information Systems, 2001, 3(3): 263-286. http://doi.ieeecomputersociety.org/resolve?ref_id=doi:10.1007/PL00011669&rfr_id=trans/tk/2008/12/ttk2008121616.htm
[17]	LIN J, KHADE R, LI Y. Rotation-invariant similarity in time series using bag-of-patterns representation[J]. Journal of Intelligent Information Systems, 2012, 39(2): 287-315. doi: 10.1007/s10844-012-0196-5
[18]	PHAM N D, LE Q L, DANG T K.Two novel adaptive symbolic representations for similarity search in time series databases[C]//Proceedings of the 12th Asia-Pacific Web Conference (APWeb).Piscataway: IEEE Press, 2010: 181-187.
[19]	LKHAGVA B, SUZUKI Y, KAWAGOE K.New time series data representation ESAX for financial applications[C]//International Conference on Data Engineering Workshops.Piscataway: IEEE Press, 2006: 17-22.
[20]	ZHANG K, LI Y, CHAI Y, et al.Trend-based symbolic aggregate approximation for time series representation[C]//2018 Chinese Control and Decision Conference (CCDC).Piscataway: IEEE Press, 2018: 2234-2240.
[21]	陈静. 卫星遥测数据的时间序列相似性度量方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2015: 22-23. CHEN J.Similarity measure of time series for satellite telemetry data[D].Harbin: Harbin Institute of Technology, 2015: 22-23(in Chinese).