基于GPU的快速有限元法求解密度场

李果阳; 严华; 张征宇; 陈沁梅; 祝福顺

doi:10.13700/j.bh.1001-5965.2020.0346

基于GPU的快速有限元法求解密度场

doi: 10.13700/j.bh.1001-5965.2020.0346

1.
四川大学电子信息学院, 成都 610065
2.
中国空气动力研究与发展中心高速空气动力研究所, 绵阳 621000

基金项目:

国家自然科学基金 11872069

详细信息

通讯作者:
严华, E-mail: yanhua@scu.edu.cn

中图分类号: TP301.6
计量
- 文章访问数: 425
- HTML全文浏览量: 100
- PDF下载量: 127
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-21
- 录用日期: 2020-10-16
- 网络出版日期: 2021-10-20

A fast finite element method based on GPU to solve density field

1.
College of Electronics Information Engineering, Sichuan University, Chengdu 610065, China
2.
High Speed Aerdynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China

Funds:

National Natural Science Foundation of China 11872069

More Information

Corresponding author: YAN Hua, E-mail: yanhua@scu.edu.cn

摘要

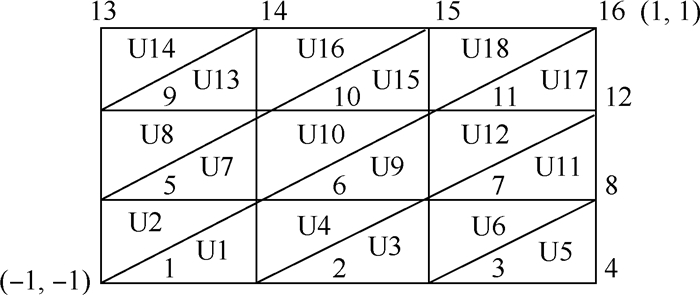
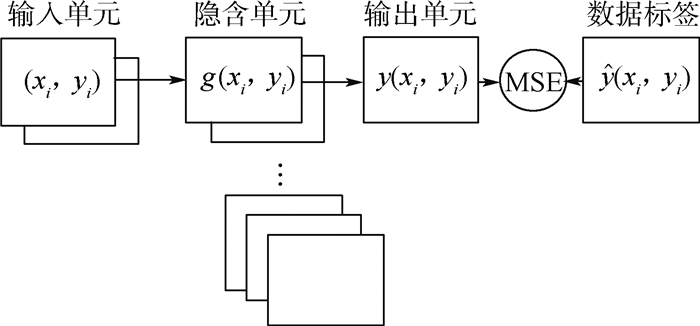
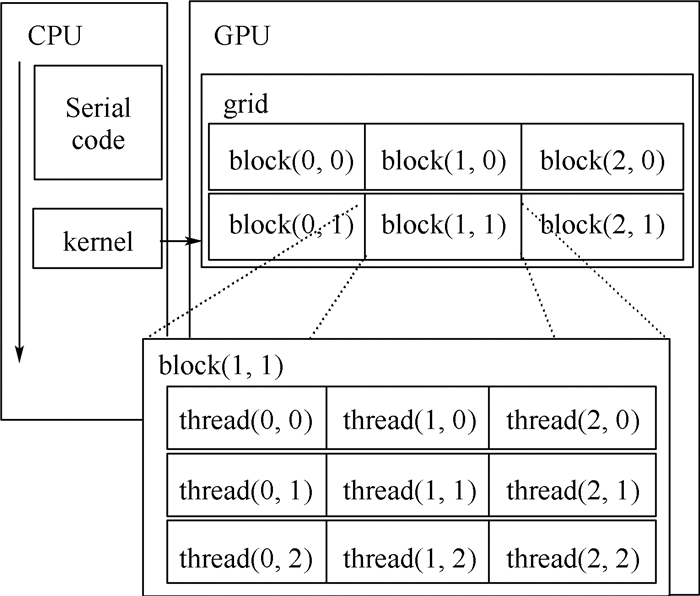
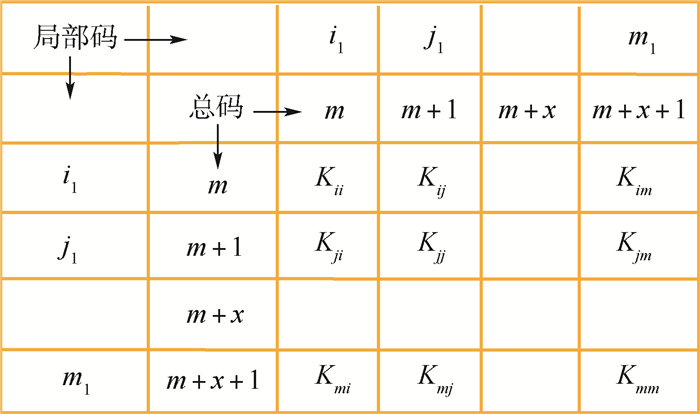
摘要:
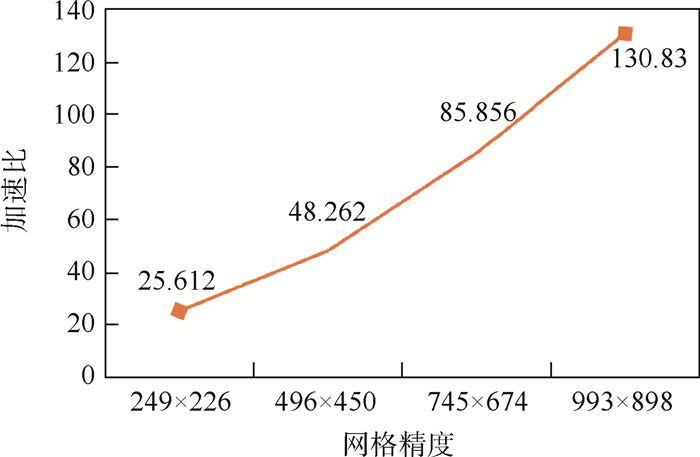
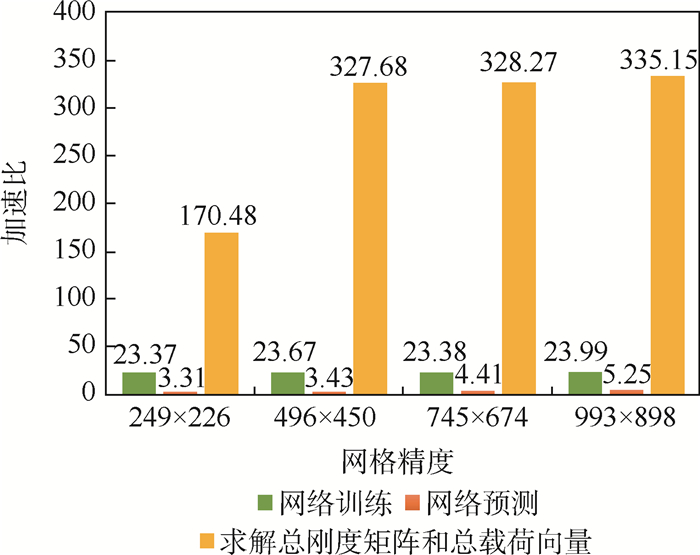
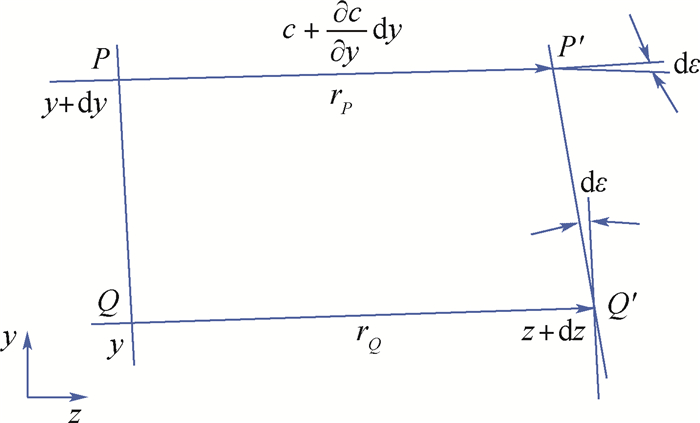
为了快速计算分析利用视频测量方法测得的高速风洞试验密度场在扰动流场作用下的实验数据，针对密度场的数值求解问题，经过光线偏折理论分析密度场得到的二阶偏微分方程，对其研究实现了CPU串行有限元法求解。在此基础上提出了基于GPU的快速有限元求解密度场的方法，该方法经过对串行有限元法求解过程效率分析后，将耗时的神经网络拟合、总刚度矩阵和总载荷向量的求解进行了基于GPU的并行加速。实验结果表明：在精度满足实际工程要求的前提下，相对于CPU串行求解方法，所提方法可大大提高求解效率，且随着网格剖分成倍加密，其加速比成倍增加。
- 密度投影场 /
- 有限元 /
- 并行加速 /
- 二阶偏微分方程 /
- 刚度矩阵
Abstract:
In order to quickly calculate and analyze the experimental data under the action of turbulence field, which are measured by video measurement method in high-speed wind tunnel test density projection field, and aimed at the numerical solution of density projection field, the second-order partial differential equation of density projection field is analyzed by ray deflection theory. And the CPU serial finite element method is realized to solve the problem. On this basis, a GPU-based fast finite element method for solving density field is proposed. After analyzing the efficiency of the serial finite element method solving process, the time-consuming neural network fitting, total stiffness matrix and total load vector are solved and then GPU-based parallel acceleration are carried out. The experimental results show that, under the premise that the accuracy meets the actual engineering requirements, the proposed method can greatly improve the solving efficiency compared with the CPU serial solution method, and the acceleration ratio is multiplied with the grid subdivision and multiplied encryption.
- density projection field /
- finite element /
- parallel acceleration /
- second-order partial differential equation /
- stiffness matrix

HTML全文

图 1 光线的偏折角分析示意图

Figure 1. Schematic diagram of ray deflection angle analysis

下载: 全尺寸图片幻灯片

图 2 网格剖分平面示意图

Figure 2. Grid subdivision plan sketch

下载: 全尺寸图片幻灯片

图 3 神经网络拟合模型

Figure 3. Neural network fitting model

下载: 全尺寸图片幻灯片

图 4 CUDA线程组织结构模型

Figure 4. CUDA thread organization structure model

下载: 全尺寸图片幻灯片

图 5 神经网络并行模型

Figure 5. Neural network parallel model

下载: 全尺寸图片幻灯片

图 6 剖分的任一网格位置结点编号

Figure 6. Node number of any grid position of subdivision

下载: 全尺寸图片幻灯片

图 7 单元刚度矩阵与总刚度矩阵位置对应关系

Figure 7. Location of element stiffness matrix corresponding to total stiffness matrix

下载: 全尺寸图片幻灯片

图 8 结点存储位置

Figure 8. Node storage location

下载: 全尺寸图片幻灯片

图 9 不同网格精度下主要模块占总运行时间的比例

Figure 9. Proportion of main modules in total running time with different grid precision

下载: 全尺寸图片幻灯片

图 10 不同网格精度下求解密度场的加速比

Figure 10. Acceleration ratio of solved density field with different grid precision

下载: 全尺寸图片幻灯片

图 11 不同网格精度下求解密度场主要模块的加速比

Figure 11. Acceleration ratio of main modules of solved density field with different grid precision

下载: 全尺寸图片幻灯片

图 12 有限元串并行精度比较

Figure 12. Serial and parallel precision comparison of finite element method

下载: 全尺寸图片幻灯片

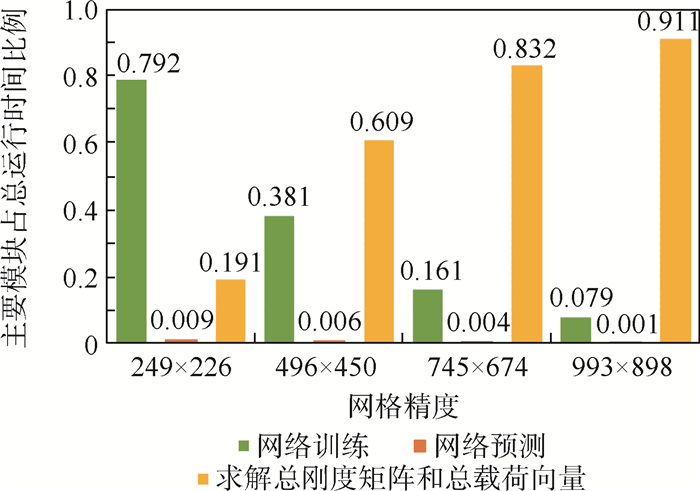
表 1 不同模块下CPU串行求解时间

Table 1. CPU serial solution time under different modules

网格精度	求解时间/s
网格精度	网络训练	网络预测	总刚度矩阵和总载荷向量	密度场
249×226	632.067	3.50	155.14	792.45
496×450	648.152	3.98	1 045.29	1 700.77
745×674	643.10	5.208	3 295.803	3 937.379
993×898	661.75	6.247	7 718.611	8 396.45

下载: 导出CSV

表 2 不同模块下GPU并行求解时间

Table 2. GPU parallel solving time under different modules

网格精度	求解时间/s
网格精度	网络训练	网络预测	总刚度矩阵和总载荷向量	密度场
249×226	27.05	1.01	0.91	30.94
496×450	27.38	1.16	3.91	35.24
745×674	27.51	1.18	10.04	45.86
993×898	27.58	1.19	23.03	64.18

下载: 导出CSV

参考文献(21)

[1]	郭隆德, 杨建军, 吴运刚, 等. 利用光学层析技术重构超声速绕流流场密度分布[J]. 实验流体力学, 2009, 23(2): 68-72. doi: 10.3969/j.issn.1672-9897.2009.02.015 GUO L D, YANG J J, WU Y G, et al. Reconstruction of density distribution in the supersonic flow field with optical computerized tomography[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(2): 68-72(in Chinese). doi: 10.3969/j.issn.1672-9897.2009.02.015
[2]	MEIER G E A. Cornputerized background oriented schlieren[J]. Experiments in Fluids, 2002, 33: 181-187. doi: 10.1007/s00348-002-0450-7
[3]	张征宇, 王显圣, 黄叙辉, 等. 高速复杂流动结构的视频测量[J]. 航空学报, 2017, 38(8): 120989. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201708003.htm ZHANG Z Y, WANG X S, HUANG X H, et al. Videogrammetry measurement for high-speed complex flow structures[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(8): 120989(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201708003.htm
[4]	张正贺, 黄贞, 陈汝婷, 等. 基于投影式背景纹影技术的火焰温度场测量仪设计[J]. 激光与光电子学进展, 2019, 56(5): 052803. https://www.cnki.com.cn/Article/CJFDTOTAL-JGDJ201905030.htm ZHANG Z H, HUANG Z, CHEN R T, et al. Design of flame temperature measurement instrument based on projective background-oriented schlieren technique[J]. Laser & Optoelectronics Progress, 2019, 56(5): 052803(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JGDJ201905030.htm
[5]	OTA M, KURIHARA K, ARIMOTO H, et al. Background oriented schlieren (BOS) measurement in supersonic flow with 4K high-speed camera[C]//Proc SPIE 10328, Selected Papers from the 31st International Congress on High-Speed Imaging and Photonics, 2017, 1032: 103281.
[6]	VERSO L, LIBERZON A. Background oriented schlieren in a density stratified fluid[J]. The Review of Scientific Instruments, 2015, 86(10): 103705. doi: 10.1063/1.4934576
[7]	张卫庆, 王成亮, 徐洪, 等. 基于有限元法的油浸式变压器绕组温度场数值模拟分析[J]. 自动化与仪器仪表, 2020(4): 56-59. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDYY202004013.htm ZHANG W Q, WANG C L, XU H, et al. Numerical simulation analysis of winding temperature field of oil-immersed transformer based on finite element method[J]. Automation & Instrumentation, 2020(4): 56-59(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDYY202004013.htm
[8]	夏一帆. 面向航空发动机燃烧室点火问题的数值计算方法研究[D]. 杭州: 浙江大学, 2019. http://cdmd.cnki.com.cn/Article/CDMD-10335-1019056476.htm XIA Y F. A study of numerical methods for the ignition process in aeroengine combustors[D]. Hangzhou: Zhejiang University, 2019(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10335-1019056476.htm
[9]	FEVGAS A, DALOUKAS K, TSOMPANOPOULOU P, et al. A study of sparse matrix methods on new hardware[J]. International Journal of Monitoring and Surveillance Technologies Research, 2015, 3(3): 1-19. doi: 10.4018/IJMSTR.2015070101
[10]	BARAN B, KÖHLER M, PRASAD N, et al. Numerical solution of large scale sparse matrix equations in python[J]. Proceedings in Applied Mathematics and Mechanics, 2014, 14(1): 959-960. doi: 10.1002/pamm.201410460
[11]	贾光辉, 于云瑞, 王丹. 卷积神经网络求解有限元单元刚度矩阵[J]. 北京航空航天大学学报, 2020, 46(3): 481-487. doi: 10.13700/j.bh.1001-5965.2019.0134 JIA G H, YU Y R, WANG D. Solving finite element stiffness matrix based on convolutional neural network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(3): 481-487(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0134
[12]	刘尧喜, 唐进元, 周炜, 等. 扩展有限元刚度矩阵的CSR存储实现[J]. 机械强度, 2019, 41(6): 1384-1390. https://www.cnki.com.cn/Article/CJFDTOTAL-JXQD201906019.htm LIU Y X, TANG J Y, ZHOU W, et al. CSR storage method of extended finite element stiffness matrix[J]. Journal of Mechanical Strength, 2019, 41(6): 1384-1390(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXQD201906019.htm
[13]	曹建伟, 徐翔, 王友年. 基于GPU求解椭圆型偏微分方程的并行算法[J]. 计算物理, 2015, 32(4): 475-481. doi: 10.3969/j.issn.1001-246X.2015.04.013 CAO J W, XU X, WANG Y N. Parallel algorithms for separable elliptic equation based on GPU[J]. Chinese Journal of Computational Physics, 2015, 32(4): 475-481(in Chinese). doi: 10.3969/j.issn.1001-246X.2015.04.013
[14]	LOH W K, KIM Y K. A GPU-accelerated density-based clustering algorithm[C]//2014 IEEE Fourth International Conference on Big Data and Cloud Computing. Piscataway: IEEE Press, 2014: 775-776.
[15]	周树荃. 有限元结构分析并行计算[M]. 北京: 科学出版社, 1994. ZHOU S Q. Parallel calculation of finite element structural analysis[M]. Beijing: Science Press, 1994(in Chinese).
[16]	张俊, 胥頔, 张龙. 基于BOS技术的密度场测量研究[J]. 实验流体力学, 2015, 29(1): 77-82. https://www.cnki.com.cn/Article/CJFDTOTAL-LTLC201501012.htm ZHANG J, XU D, ZHANG L. Research on density measurement based on background oriented schlieren method[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(1): 77-82(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LTLC201501012.htm
[17]	张俊, 胥頔, 朱博. 背景纹影技术算法研究[C]//中国空气动力学会测控技术专委会第六届四次学术交流会, 2013: 68-73. ZHANG J, XU D, ZHU B. Background schlieren technique algorithm research[C]//The Chinese Society of Aerodynamic Control Technology of the 6th Four Academic Conference Proceedings, 2013: 68-73(in Chinese).
[18]	陈国荣. 有限单元法原理及应用[M]. 2版. 北京: 科学出版社, 2016: 91-116. CHEN G R. Principle and application of finite element method[M]. 2nd ed. Beijing: Science Press, 2016: 91-116(in Chinese).
[19]	朱道建. 利用有限元方法求解流体动力学问题[D]. 武汉: 武汉大学, 2017. http://cdmd.cnki.com.cn/article/cdmd-10486-1017195645.htm ZHU D J. To solve the fluid dynamics problems by finite element method[D]. Wuhan: Wuhan University, 2017(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10486-1017195645.htm
[20]	张健飞, 沈德飞. 有限元GPU加速计算的实现方法[J]. 计算机辅助工程, 2014, 23(2): 41-45. https://www.cnki.com.cn/Article/CJFDTOTAL-JSFZ201402010.htm ZHANG J F, SHEN D F. Implementation method of GPU-accelerated finite element calculation[J]. Computer Aided Engineering, 2014, 23(2): 41-45(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSFZ201402010.htm
[21]	KIRK D B, HWU W W. Programming massively parallel processors: A hands-on approach[M]. 2nd ed. New York: Morgan Kaufmann, 2010: 19-130.