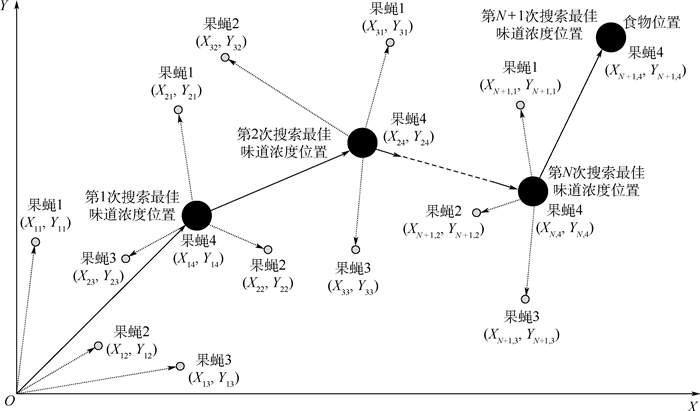
-
摘要:
为提高微机电系统（MEMS）加速度计的标定效率并降低对高精度转台的依赖，提出一种基于改进果蝇优化算法（IFOA）的MEMS加速度计无转台标定方法。首先，根据模观测标定法原理将加速度计标定问题转化为非线性函数优化问题。然后，针对经典果蝇优化算法存在的只能搜索正参数及搜索步长固定的不足，对味道浓度判定值及搜索步长进行改进，使改进后的算法具有全局参数搜索及可变步长2种性能，并利用Rosenbrock函数进行测试，结果表明，IFOA相比于经典果蝇优化算法具有全局参数寻优范围及更高的寻优精度。最后，将IFOA应用于求解加速度计待标定参数的非线性函数优化问题，并将结果与牛顿迭代法和粒子群优化（PSO）算法进行对比。仿真结果表明：IFOA在求解精度方面比牛顿迭代法提高了1~3个数量级；在运行稳定性方面比牛顿迭代法和PSO算法分别提高了30%和34%，在运行时间方面分别减小了15.2%和43.6%；在加速度计无转台标定方面具有良好的应用价值。
-
关键词:
- 微机电系统(MEMS) /
- 加速度计 /
- 标定 /
- 模观测法 /
- 果蝇优化算法(FOA)
Abstract:In order to improve the calibration efficiency of Micro-Electro-Mechanical System (MEMS) accelerometers and reduce the dependence on high-precision turntables, a MEMS accelerometer calibration method based on Improved Fruit Fly Optimization Algorithm (IFOA) without turntables is proposed. The method first converts the accelerometer calibration problem into a nonlinear function optimization problem according to the principle of norm-observation. Afterwards, in view of the shortcomings of the classic FOA that can only search for positive parameters and search step size is fixed, the smell concentration judgment value and search step size were improved to make IFOA have global parameter search and variable step size. The two improved performances were tested using the Rosenbrock function. The results show that the IFOA has a global parameter optimization range and higher optimization accuracy than the classic FOA. Finally, the IFOA was applied to solve the nonlinear function optimization problem of accelerometer calibration parameters. The results are compared with those of Newton iteration method and Particle Swarm Optimization (PSO) algorithm. The simulation results show that the IFOA is 1-3 orders of magnitude higher than Newton iteration method in terms of solution accuracy. Compared with Newton iteration method and PSO algorithm, the IFOA improves the running stability by 30% and 34% respectively, and reduces the running time by 15.2% and 43.6% respectively. The IFOA has a good application value in the calibration of accelerometer without turntable
-
图 3 多种群IFOA示意图
Figure 3. Schematic diagram of multi-population improved fruit fly optimization algorithm
图 4 三种果蝇优化算法收敛曲线
Figure 4. Convergence curves of three fruit fly optimization algorithms
表 1 三种果蝇优化算法计算得到的平均值
Table 1. Calculated mean of three fruit fly optimization algorithms
参数 果蝇优化算法 全参数果蝇优化算法 全参数变步长果蝇优化算法 x1 7.167 8 -0.999 4 -0.999 9 x2 0.427 1 -0.998 8 -0.999 7 x3 0.059 3 -0.997 5 -0.999 4 f(x) 40.427 6.17×10-4 3.70×10-7 
下载: 导出CSV
表 2 三种果蝇优化算法计算得到的均方根误差
Table 2. Calculated root mean square error of three fruit fly optimization algorithms
参数 果蝇优化算法 全参数果蝇优化算法 全参数变步长果蝇优化算法 x1 8.437 9 7.00×10-3 2.71×10-4 x2 1.428 4 1.41×10-2 5.40×10-4 x3 1.059 3 2.86×10-2 1.10×10-3 f(x) 52.055 1.10×10-3 1.87×10-6
下载: 导出CSV
表 3 三种优化算法加速度计各参数标定结果及标定误差
Table 3. Calibration results and calibration errors of three optimization algorithms for parameters of accelerometer
标定参数 真值 牛顿迭代法 PSO算法 IFOA 标定值 相对误差/% 标定值 相对误差/% 标定值 相对误差/% 刻度因子 Sxa 4.587 40×105 4.587 39×105 -0.000 2 4.587 40×105 0 4.587 40×105 0 Sya 4.562 80×105 4.562 80×105 0 4.562 80×105 0 4.562 80×105 0 Sza 4.528 40×105 4.528 40×105 0 4.528 40×105 0 4.528 40×105 0 安装误差 γyza -7.153 94×10-4 -7.254 45×10-4 1.405 0 -7.153 88×10-4 -0.000 8 -7.153 35×10-4 -0.008 2 γzya 1.032 88×10-3 1.026 89×10-3 -0.579 9 1.032 89×10-3 0.001 0 1.032 85×10-3 -0.002 9 γzxa 1.405 49×10-3 1.410 14×10-3 0.330 8 1.405 48×10-3 -0.000 7 1.405 51×10-3 0.001 4 零偏 bxa -4.274 80×103 -4.276 02×103 0.028 5 -4.274 79×103 -0.000 2 -4.274 81×103 0.000 2 bya -2.354 20×104 -2.354 31×104 0.004 7 -2.354 20×104 0 -2.354 20×104 0 bza -4.478 20×103 -4.475 34×103 -0.063 9 -4.478 21×103 0.000 2 -4.478 14×103 -0.001 3
下载: 导出CSV
表 4 三种优化算法标定平均运行时间及成功率
Table 4. Average calibration time and success rate of three optimization algorithms
优化算法 标定平均运行时间/s 标定成功率/% 牛顿迭代法 8.36 70 PSO算法 12.56 66 IFOA 7.09 100
下载: 导出CSV
-
[1] CIUTI G, RICOTTI L, MENCIASSI A, et al. MEMS sensor technologies for human centred applications in healthcare, physical activities, safety and environmental sensing: A review on research activities in Italy[J]. Sensors, 2015, 15(3): 6441-6468. doi: 10.3390/s150306441 [2] LIU Y, XIANG G, LU Y, et al. Calibration of MEMS accelerometer based on Kalman filter and the improved six position method[J]. Journal of Communications, 2016, 11(5): 516-522. [3] NEZ A, FRADET L, LAGUILLAUMIE P, et al. Comparison of calibration methods for accelerometers used in human motion analysis[J]. Medical Engineering, 2016, 38(11): 1289-1299. doi: 10.1016/j.medengphy.2016.08.004 [4] HE G L, TAO S Q, SHEN Q, et al. Research on calibration and parameter compensation of MEMS inertial sensors based on error analysis[C]//2012 Fifth International Symposium on Computational Intelligence and Design. Piscataway: IEEE Press, 2012: 325-329. [5] 田晓春, 李杰, 范玉宝, 等. 一种微惯性测量单元标定补偿方法[J]. 传感技术学报, 2012, 25(10): 1411-1415. doi: 10.3969/j.issn.1004-1699.2012.010.017TIAN X C, LI J, FAN Y B, et al. A calibration-compensation method for micro inertial measurement unit[J]. Chinese Journal of Sensors and Actuators, 2012, 25(10): 1411-1415(in Chinese). doi: 10.3969/j.issn.1004-1699.2012.010.017 [6] 于婷, 孙伟, 文剑. MEMS惯性组件的误差特性分析与标定[J]. 传感技术学报, 2016, 29(6): 859-864. doi: 10.3969/j.issn.1004-1699.2016.06.012YU T, SUN W, WEN J. Error analysis and calibration of MEMS inertial components[J]. Chinese Journal of Sensors and Actuators, 2016, 29(6): 859-864(in Chinese). doi: 10.3969/j.issn.1004-1699.2016.06.012 [7] LÖTTERS J C, SCHIPPER J, VELTINK P H, et al. Procedure for in-use calibration of triaxial accelerometers in medical applications[J]. Journal of Applied Behavior Analysis, 1998, 68(1-3): 221-228. [8] SKOG I, HÄNDEL P. Calibration of a MEMS inertial measurement unit[C]//XVII IMEKO World Congress, 2006: 1-6. [9] FROSIO I, PEDERSINI F, BORGHESE N A, et al. Autocalibration of MEMS accelerometers[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(6): 2034-2041. doi: 10.1109/TIM.2008.2006137 [10] QURESHI U, GOLNARAGHI F. An algorithm for the in-field calibration of a MEMS IMU[J]. IEEE Sensors Journal, 2017, 17(22): 7479-7486. doi: 10.1109/JSEN.2017.2751572 [11] SIPOS M. Analyses of triaxial accelerometer calibration algorithms[J]. IEEE Sensors Journal, 2012, 12(5): 1157-1165. doi: 10.1109/JSEN.2011.2167319 [12] CAI Q, SONG N, YANG G, et al. Accelerometer calibration with nonlinear scale factor based on multi-position observation[J]. Measurement Science, 2013, 24(10): 105002. doi: 10.1088/0957-0233/24/10/105002 [13] 戴邵武, 王克红, 戴洪德. 基于PSO算法的加速度计快速标定方法[J]. 电光与控制, 2014, 21(12): 57-60. doi: 10.3969/j.issn.1671-637X.2014.12.013DAI S W, WANG K H, DAI H D. A rapid calibration method for accelerometer based on PSO algorithm[J]. Elctronics Optics & Control, 2014, 21(12): 57-60(in Chinese). doi: 10.3969/j.issn.1671-637X.2014.12.013 [14] PODDAR S, KUMAR A. Scale-free PSO for in-run and infield inertial sensor calibration[J]. Measurement, 2019, 147: 106849. doi: 10.1016/j.measurement.2019.07.077 [15] 杨管金子, 李建辰, 黄海, 等. 基于遗传算法的加速度计免转台标定方法[J]. 中国惯性技术学报, 2017, 25(1): 119-123. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGXJ201701024.htmYANG G J Z, LI J C, HUANG H, et al. Non-turntable calibration method for three-accelerometer based on genetic algorithm[J]. Journal of Chinese Inertial Technology, 2017, 25(1): 119-123(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGXJ201701024.htm [16] CUI X, LIU C, SHI G, et al. A new calibration method for MEMS accelerometers with genetic algorithm[C]//2017 IEEE International Conference on Real-Time Computing and Robotics (RCAR). Piscataway: IEEE Press, 2017: 240-245. [17] 高爽, 张若愚. 基于自适应遗传算法的MEMS加速度计快速标定方法[J]. 北京航空航天大学学报, 2019, 45(10): 1982-1989. doi: 10.13700/j.bh.1001-5965.2019.0040GAO S, ZHANG R Y. Rapid calibration method of MEMS accelerometer based on adaptive GA[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(10): 1982-1989(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0040 [18] WANG D, TAN D, LIU L. Particle swarm optimization algorithm: An overview[J]. Soft Computing, 2018, 22(2): 387-408. doi: 10.1007/s00500-016-2474-6 [19] PAN W T. A new fruit fly optimization algorithm: Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74. doi: 10.1016/j.knosys.2011.07.001 [20] DAI H, ZHAO G, LU J, et al. Comment and improvement on "A new fruit fly optimization algorithm: Taking the financial distress model as an example"[J]. Knowledge-Based Systems, 2014, 59: 159-160. doi: 10.1016/j.knosys.2014.01.010 [21] DAI H, LIU A, LU J, et al. Optimization about the layout of IMUs in large ship based on fruit fly optimization algorithm[J]. Optik, 2015, 126(4): 490-493. doi: 10.1016/j.ijleo.2014.08.037 [22] WANG L, XIONG Y, LI S, et al. New fruit fly optimization algorithm with joint search strategies for function optimization problems[J]. Knowledge-Based Systems, 2019, 176: 77-96. doi: 10.1016/j.knosys.2019.03.028 [23] 赵晓军, 刘成忠, 胡小兵. 基于果蝇优化算法的PID控制器设计与应用[J]. 中南大学学报(自然科学版), 2016, 47(11): 3729-3734. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201611016.htmZHAO X J, LIU C Z, HU X B. Design and application of PID controller based on fruit fly optimization algorithm[J]. Journal of Central South University (Science and Technology), 2016, 47(11): 3729-3734(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201611016.htm [24] JIANG W, WU X, GONG Y, et al. Holt-Winters smoothing enhanced by fruit fly optimization algorithm to forecast monthly electricity consumption[J]. Energy, 2020, 193: 116779. doi: 10.1016/j.energy.2019.116779 [25] SHI K, ZHANG X, XIA S. Multiple swarm fruit fly optimization algorithm based path planning method for Multi-UAVs[J]. Applied Sciences, 2020, 10(8): 2822. doi: 10.3390/app10082822 [26] PODDAR S, KUMAR V, KUMAR A. A comprehensive overview of inertial sensor calibration techniques[J]. Journal of Dynamic Systems, Measurement, and Control, 2017, 139(1): 011006. doi: 10.1115/1.4034419 [27] SHIN E H, EL-SHEIMY N. A new calibration method for strapdown inertial navigation systems[J]. Z. Vermess, 2002, 127: 1-10. [28] FONG W, ONG S, NEE A. Methods for in-field user calibration of an inertial measurement unit without external equipment[J]. Measurement Science and Technology, 2008, 19(8): 085202. doi: 10.1088/0957-0233/19/8/085202 [29] ZHANG H, WU Y, WU W, et al. Improved multi-position calibration for inertial measurement units[J]. Measurement Science and Technology 2010, 21(1): 015107. doi: 10.1088/0957-0233/21/1/015107 [30] MA J, LI H. Research on Rosenbrock function optimization problem based on improved differential evolution algorithm[J]. Journal of Computer Communications, 2019, 7(11): 107-120. doi: 10.4236/jcc.2019.711008 -
下载:
点击查看大图
计量
- 文章访问数: 652
- HTML全文浏览量: 236
- PDF下载量: 133
- 被引次数: 0
