二维功能梯度壁板热颤振本征问题的精确解

代林桐; 邢誉峰

doi:10.13700/j.bh.1001-5965.2020.0351

二维功能梯度壁板热颤振本征问题的精确解

doi: 10.13700/j.bh.1001-5965.2020.0351

代林桐,
邢誉峰^,

北京航空航天大学固体力学所, 北京 100083

基金项目:

国家自然科学基金 11672019

详细信息

通讯作者:
邢誉峰, E-mail: xingyf@buaa.edu.cn

中图分类号: V221⁺.3;TB553
计量
- 文章访问数: 460
- HTML全文浏览量: 82
- PDF下载量: 38
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-21
- 录用日期: 2020-08-21
- 网络出版日期: 2021-10-20

Exact solutions of thermal flutter of two-dimensional functionally graded panel

DAI Lintong,
XING Yufeng^,

Institute of Solid Mechanics, Beihang University, Beijing 100083, China

Funds:

National Natural Science Foundation of China 11672019

More Information

Corresponding author: XING Yufeng, E-mail: xingyf@buaa.edu.cn

摘要

摘要:
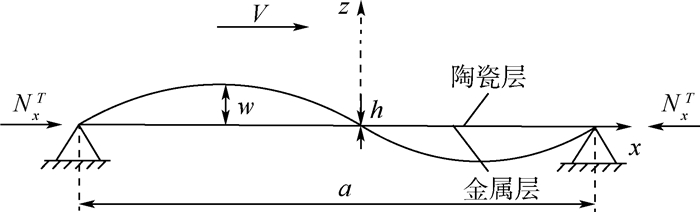
为了得到二维功能梯度壁板热颤振的精确解并揭示颤振机理，根据经典薄板理论及一阶活塞理论，建立了超声速气流下二维功能梯度壁板的本征控制微分方程并求得了精确解，根据得到的本征根对颤振机理进行了分析。针对功能梯度材料（FGM）的不同体积分数，分别研究了壁板在恒温场及非线性温度场下的颤振边界随马赫数的变化规律，并比较了2种温度场下的结果。通过分析简支、固支及其组合边界情况下的壁板颤振特性，从数学角度发现颤振现象的发生是由于挠度的一阶导数导致刚度非对称，且功能梯度材料能够有效提高热环境下壁板的颤振边界，同时利用ABAQUS软件对功能梯度壁板的振动特性进行了模拟，进一步验证了所提方法的有效性。
- 超声速 /
- 功能梯度材料(FGM) /
- 热颤振 /
- 本征根 /
- 精确解
Abstract:
For achieving the thermal flutter exact solutions of two-dimensional functionally graded panel and revealing the mechanism of the thermal flutter, based on the classical thin plate theory and the first-order piston theory, the characteristic governing differential equation of two-dimensional functionally graded panel in supersonic flow is established and exact solutions are obtained. Through the analysis of the eigenvalues, the mechanism of the panel flutter is investigated. According to different volume fraction of Functionally Graded Materials (FGM), the flutter boundary changes with Mach number in constant temperature field and nonlinear temperature field are studied respectively, and the results in two temperature fields are compared. By analyzing the flutter characteristics of panels with simply supported, fixed and integrated edges, it can be concluded that the flutter phenomenon is caused by the first-order derivative of deflection which leads to the asymmetry of system stiffness, and FGM can effectively improve the flutter boundary of the panel in the thermal environment. Meanwhile, the vibration properties of the FGM panel is simulated with ABAQUS, further validating the effectiveness of the present method.
- supersonic /
- Functionally Graded Materials (FGM) /
- thermal flutter /
- eigenvalue /
- exact solution

HTML全文

图 1 两端简支壁板几何模型

Figure 1. Geometric model of simply supported panel at both ends

下载: 全尺寸图片幻灯片

图 2 临界动压值随梯度指数变化曲线

Figure 2. Critical dynamic pressure versus gradient index

下载: 全尺寸图片幻灯片

图 3 临界颤振频率随温度的变化曲线

Figure 3. Critical flutter frequency versus temperature

下载: 全尺寸图片幻灯片

图 4 两种热环境下频率随马赫数的变化曲线

Figure 4. Frequency versus Mach number in two thermal environments

下载: 全尺寸图片幻灯片

表 1 简支和固支边界条件

Table 1. Boundary conditions for simple support and clamp

BCs(边界条件)	x=0或x=a
简支(S)	w=0，
固支(C)	w=0,

下载: 导出CSV

表 2 二维壁板颤振频率方程和本征函数

Table 2. Eigensolutions of two-dimensional panel flutters

BCs	频率方程	本征函数的系数
简支-简支(SS) ϕ(0)=0 ϕ(1)=0 ϕ″(0)=0 ϕ″(1)=0
固支-固支(CC) ϕ(0)=0 ϕ(1)=0 ϕ′(0)=0 ϕ′(1)=0
简支-固支(SC) ϕ(0)=0 ϕ″(0)=0 ϕ(1)=0 ϕ′(1)=0	4ϑα₁β₁sinh 2ϑ-β₁(4ϑ²-α₁²-β₁²)sin α₁cosh β₁-α₂(4ϑ²+α₁²+β₁²)cos α₁sinh β₁=0

下载: 导出CSV

表 3 功能梯度材料弹性常数

Table 3. Elastic constants of FGM

材料名称	组成成分	E/GPa	υ	ρ/(kg·m^-3)
陶瓷金属	Si₃N₄(氮化硅陶瓷)	322	0.24	2 370
陶瓷金属	SUS304(不锈钢)	207	0.32	8 166

下载: 导出CSV

表 4 分层为5层时密度和弹性模量

Table 4. Density and modulus of elasticity for 5 layers

坐标方向	厚度方向坐标/(10^-4m)	密度/(kg·m^-3)	弹性模量/(10¹¹Pa)
z	-8.000	8 165.942	2.070
z	-4.000	8 151.916	2.073
z	0	7 984.875	2.106
z	4.000	7 191.866	2.263
z	8.000	4 743.520	2.749

下载: 导出CSV

表 5 分层为10层时密度和弹性模量

Table 5. Density and modulus of elasticity for 10 layers

坐标方向	厚度方向坐标/(10^-4m)	密度/(kg·m^-3)	弹性模量/(10¹¹Pa)
z	-9.000	8 165.998	2.070
z	-7.000	8 165.560	2.070
z	-5.000	8 160.340	2.071
z	-3.000	8 135.558	2.076
z	-1.000	8 059.047	2.091
z	1.000	7 874.296	2.127
z	3.000	7 493.496	2.203
z	5.000	6 790.582	2.343
z	7.000	5 594.284	2.580
z	9.000	3 681.166	2.959

下载: 导出CSV

表 6 不同边界条件下FGM板频率

Table 6. Frequency of FGM plate under different boundary conditions

边界条件	模态阶数	频率/Hz
边界条件	模态阶数	精确解	ABAQUS(5层)	ABAQUS(10层)
SS	1	131.679 3	129.345 7	131.010 7
SS	2	523.997 7	517.596 2	521.925 4
CC	1	296.864 6	293.355 6	295.806 1
CC	2	818.792 2	808.520 3	815.306 1
SC	1	204.444 7	202.048 4	203.851 7
SC	2	663.293 8	654.707 9	660.551 3

下载: 导出CSV

表 7 本文解与Galerkin方法结果的对比

Table 7. Comparison of result between present method and Galerkin method

方法	固有频率(Ma=2)		颤振参数
方法	ω₁/Hz	ω₂ /Hz	ω_f /Hz	Ma_f
Galerkin	650.725 8	2 130.318 9	1 773.443 7	7.177 4
本文	651.975 4	2 130.663 1	1 759.928 3	6.989 6

下载: 导出CSV

表 8 不同边界下FGM板的临界颤振频率和临界动压的比较

Table 8. Comparison of flutter frequency and critical dynamic pressure of FGM plate under different boundary conditions

T/K	n	SS		CC		SC
T/K	n	λ^*	ω^*	λ^*	ω^*	λ^*	ω^*
T_t=300 T_b=300	1	434.22	26.0	788.45	41.7	594.19	33.3
	5	388.51	21.1	719.89	34.1	548.49	27.3
	50	354.23	19.0	651.33	30.6	491.35	24.5
T_t=500 T_b=300	1	399.94	24.8	754.17	40.7	571.34	32.4
	5	365.66	20.2	685.61	33.2	514.21	26.3
	50	319.95	17.9	617.05	29.7	457.07	23.4
T_t=500 T_b=500	1	365.66	23.4	708.46	39.3	525.63	30.9
	5	331.38	18.9	639.90	31.9	479.93	25.1
	50	285.67	16.6	571.34	28.5	422.79	22.3

下载: 导出CSV

参考文献(19)

[1]	杨智春, 夏巍, 孙浩. 高速飞行器壁板颤振分析的研究进展[J]. 结构强度研究, 2005(4): 10-18. https://www.zhangqiaokeyan.com/academic-journal-cn_structural-strength-study_thesis/0201262250583.html YANG Z C, XIA W, SUN H. Research progress on flutter analysis of high speed aircraft panel[J]. Study on Structural Strength, 2005(4): 10-18(in Chinese). https://www.zhangqiaokeyan.com/academic-journal-cn_structural-strength-study_thesis/0201262250583.html
[2]	王江峰, 伍贻兆, 季卫栋, 等. 高超声速复杂气动问题数值方法研究进展[J]. 航空学报, 2015, 36(1): 159-175. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201501012.htm WANG J F, WU Y Z, JI W D, et al. Progress in numerical simulation techniques of hypersonic aerodynamic problems[J]. Acta Aeronautics et Astronautics Sinica, 2015, 36(1): 159-175(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201501012.htm
[3]	PRAVEEN G N, REDDY J N. Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates[J]. International Journal of Solids and Structures, 1998, 35(33): 4457-4476. doi: 10.1016/S0020-7683(97)00253-9
[4]	苑凯华, 邱志平. 压电复合材料壁板颤振的控制[J]. 北京航空航天大学学报, 2009, 35(12): 1429-1433. https://bhxb.buaa.edu.cn/CN/Y2009/V35/I12/1429 YUAN K H, QIU Z P. Flutter control of composite panels with embedded piezoelectric materials[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(12): 1429-1433(in Chinese). https://bhxb.buaa.edu.cn/CN/Y2009/V35/I12/1429
[5]	HOSSEINI M, FAZELZADEH S A, MARZOCCA P. Chaotic and bifurcation dynamic behavior of functionally graded curved panels under aero-thermal loads[J]. International Journal of Bifurcation and Chaos, 2011, 21(3): 931-954. doi: 10.1142/S0218127411028738
[6]	李丽丽, 赵永辉. 超音速下热壁板的颤振分析[J]. 动力学与控制学报, 2012, 10(1): 67-70. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXK201201016.htm LI L L, ZHAO Y H. The flutter analysis of thermal panel under supersonic flow[J]. Journal of Dynamics and Control, 2012, 10(1): 67-70(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLXK201201016.htm
[7]	SHAHVERDI H, KHALAFI V. Bifurcation analysis of FG curved panels under simultaneous aerodynamic and thermal loads in hypersonic flow[J]. Composite Structures, 2016, 146: 84-94. doi: 10.1016/j.compstruct.2016.03.011
[8]	黄小林, 王熙, 董雷, 等. 超音速气流中贴压电层的功能梯度材料混合板的颤振分析[J]. 应用力学学报, 2019, 36(6): 1429-1434. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201906027.htm HUANG X L, WANG X, DONG L, et al. Flutter analysis of functionally graded hybrid plates with piezoelectric layer in supersonic flow[J]. Chinese Journal of Applied Mechanics, 2019, 36(6): 1429-1434(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201906027.htm
[9]	DOWELL E H. Nonlinear oscillations of a fluttering plate. Ⅱ[J]. AIAA Journal, 1967, 5(10): 1856-1862. doi: 10.2514/3.4316
[10]	CHAKRAVERTY S, PRADHAN K K. Free vibration of exponential functionally graded rectangular plates in thermal environment with general boundary conditions[J]. Aerospace Science and Technology, 2014, 36: 132-156. doi: 10.1016/j.ast.2014.04.005
[11]	LI F M, SONG Z G. Aeroelastic flutter analysis for 2D Kirchhoff and Mindlin panels with different boundary conditions in supersonic airflow[J]. Acta Mechanica, 2014, 225(12): 3339-3351. doi: 10.1007/s00707-014-1141-1
[12]	HEDGEPETH J M. Flutter of rectangular simply supported panels at high supersonic speeds[J]. Journal of the Aeronautical Sciences, 1957, 24(8): 563-573. doi: 10.2514/8.3908
[13]	SUN Q Z, XING Y F. Exact eigensolutions for flutter of two-dimensional symmetric cross-ply composite laminates at high supersonic speeds[J]. Composite Structures, 2018, 183: 358-370. doi: 10.1016/j.compstruct.2017.03.085
[14]	SOHN K J, KIM J H. Structural stability of functionally graded panels subjected to aero-thermal loads[J]. Composite Structures, 2008, 82(3): 317-325. doi: 10.1016/j.compstruct.2007.07.010
[15]	AZADI M. Free and forced vibration analysis of FG beam considering temperature dependency of material properties[J]. Journal of Mechanical Science and Technology, 2011, 25(1): 69-80. doi: 10.1007/s12206-010-1015-y
[16]	LI Q, IU V P, KOU K P. Three-dimensional vibration analysis of functionally graded material plates in thermal environment[J]. Journal of Sound and Vibration, 2009, 324(3-5): 733-750. doi: 10.1016/j.jsv.2009.02.036
[17]	CHI S H, CHUNG Y L. Corrigendum to "Mechanical behavior of functionally graded material plates under transverse load-Part Ⅱ: Numerical results"[J]. International Journal of Solids and Structures, 2007, 44(5): 1691. https://www.sciencedirect.com/science/article/pii/S0020768306003179
[18]	XU T F, XING Y F. Closed-form solutions for free vibration of rectangular FGM thin plates resting on elastic foundation[J]. Acta Mechanica Sinica, 2016, 32(6): 1088-1103. http://qikan.cqvip.com/Qikan/Article/Detail?id=7000104591
[19]	HOUBOLT J C. A study of several aerothermoelastic problems of aircraft structures in high-speed flight[D]. Verlag Leemann Zurich: ETH Zurich, 1958: 69-71.