Time delay feedback control for transonic flutter of airfoil with free-play nonlinearity
-
摘要:
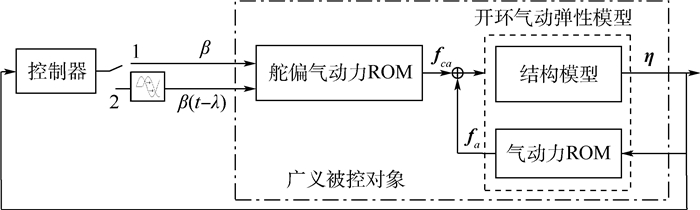
颤振主动控制会引入时滞，对气动弹性系统闭环稳定性具有显著影响。针对当前考虑时滞的机翼颤振主动控制多集中在亚、超声速域，采用线性气动力分析的研究现状，结合现代飞机大都以跨声速巡航、控制面偏转为作动器进行主动控制的应用特点，发展了考虑结构间隙非线性，基于气动力降阶模型的跨声速颤振时滞反馈主动控制方法。首先，以白噪声为激励信号，辨识得到跨声速下非定常气动力降阶模型，与间隙非线性结构模型耦合，构建被控对象状态空间模型；然后，通过一种含积分项的状态变换将输入信号存在时滞的被控系统转化为无时滞的系统；最后，采用最优控制理论设计最优时滞反馈控制。仿真结果表明：对于含时滞的系统，若施加不考虑时滞影响的控制方法，则无法抑制颤振，所提控制方法的有效性不受时滞大小的影响，可有效抑制颤振的发生。
Abstract:In active control of flutter, time delays are inevitably introduced and have significant influence on the stability of the closed-loop controlled aeroelastic system. At present, study on the flutter suppression has been focused on subsonic and supersonic regimes, where aerodynamic forces are modeled with the linear theory. However, it is noticed that civil or military aircraft usually cruise at the transonic regime, and the control surface deflection is used as a control variable in the active control. In view of the above situation, the method of time delay feedback control for free-play nonlinear system transonic flutter is developed based on the aerodynamic forces reduced order modeling. In the method, the unsteady aerodynamic forces models for transonic regime were firstly identified with the white noise as excitation signals, and were combined with free-play nonlinear structure model to construct the state-space models for the controlled aeroelastic system. Then, a state transformation with the integral item was introduced to make the input-delay system be transformed into a system without delay. Finally, optimum time delay feedback control is designed by optimum control theory. Simulation results indicate that, for the system with time delay, the control algorithm may fail to suppress the flutter if time delay is not considered in control design. The effectiveness of the proposed time delay feedback control algorithm isn't influenced by the magnitude of the time delays. The developed method can obtain excellent flutter suppression results with either small or large input time delay.
-
Key words:
- flutter suppression /
- time delay system /
- feedback control /
- transonic /
- reduced-order model /
- free-play nonlinearity
-
图 4 3211信号激励下ROM和CFD计算的气动力结果比较
Figure 4. Comparison of aerodynamic forces with ROM and CFD excited by 3211 signals
图 5 ROM和CFD结算结构响应结果比较(Ma∞=0.8U*=1.48)
Figure 5. Comparison of structure response result with ROM and CFD(Ma∞=0.8U*=1.48)
图 7 俯仰方向极限环振荡(Ma∞=0.8U*=1.48)
Figure 7. Limit-cycle oscillation of pitch at Ma∞=0.8U*=1.48
图 8 3211信号控制面偏转输入控制面ROM和CFD计算的气动力结果比较
Figure 8. Comparison of control surface aerodynamic forces with ROM and CFD excited by 3211 deflection input signals
图 11 时滞系统的无时滞控制相平面图及控制面偏转角
Figure 11. Phase portrait of no delay control for system with time delay and corresponding control surface deflection
图 12 考虑时滞的控制器对时滞系统颤振控制的相平面图及控制面偏转角(λ=0.37)
Figure 12. Phase portrait of flutter control for system with time delay exerted by controller designed with time delay and corresponding control surface deflection at λ=0.37
图 13 考虑时滞的控制器对时滞系统颤振控制的相平面图及控制面偏转角(λ=1.6)
Figure 13. Phase portrait of flutter control for system with time delay exerted by controller designed with time delay and corresponding control surface deflection at λ=1.6
表 1 模型无量纲参数
Table 1. Non-dimensional parameters of model
参数 数值 xα 0.25 rα 0.629 ωh/ωα 0.708 μ 36.15 δ 0.001 745 
下载: 导出CSV
-
[1] 王在华, 胡海岩. 时滞动力系统的稳定性与分岔: 从理论走向应用[J]. 力学进展, 2013, 43(1): 3-20. https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201301002.htmWANG Z H, HU H Y. Stability and bifurcation of delayed dynamic systems: From theory to application[J]. Advances in Mechanics, 2013, 43(1): 3-20(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201301002.htm [2] 胡海岩, 赵永辉, 黄锐. 飞机结构气动弹性分析与控制研究[J]. 力学学报, 2016, 48(1): 1-27. doi: 10.3969/j.issn.1006-6616.2016.01.001HU H Y, ZHAO Y H, HUANG R. Studies on aeroelastic analysis and control of aircraft structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 1-27(in Chinese). doi: 10.3969/j.issn.1006-6616.2016.01.001 [3] ZHAO Y H. Stability of a time-delayed aeroelastic system with a control surface[J]. Aerospace Science and Technology, 2011, 15(1): 72-77. doi: 10.1016/j.ast.2010.05.008 [4] HUANG R, HI H Y, ZHAO Y H. Designing active flutter suppression for high-dimensional aeroelastic systems involving a control delay[J]. Journal of Fluids and Structures, 2012, 34: 33-50. doi: 10.1016/j.jfluidstructs.2012.05.012 [5] LUO M X, GAO M Z, CAI G P. Delayed full-state feedback control of airfoil flutter using sliding mode control method[J]. Journal of Fluids and Structures, 2016, 61: 262-273. doi: 10.1016/j.jfluidstructs.2015.11.012 [6] GAP M Z, CAI G P. Finite-time fault-tolerant control for flutter involving control delay[J]. Journal of the Franklin Institute, 2016, 353(9): 2009-2029. doi: 10.1016/j.jfranklin.2016.03.010 [7] XU B, ZHANG W, MA J. Stability and Hopf bifurcation of a two-dimensional supersonic airfoil with a time-delayed feedback control surface[J]. Nonlinear Dynamics, 2014, 77(3): 1-19. [8] RAMESH M, NARAYANAN S. Controlling chaotic motions in a two-dimensional airfoil using time-delayed feedback[J]. Journal of Sound and Vibration, 2001, 239(5): 1037-1049. doi: 10.1006/jsvi.2000.3181 [9] MARZOCCA P, LIBRESU L, SILVA W A. Time-delay effects on linear/nonlinear feedback control of simple aeroelastic systems[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(1): 53-62. doi: 10.2514/1.4335 [10] ARAUJO J M, SANTOS T L M. Control of second-order asymmetric systems with time delay: Smith predictor approach[J]. Mechanical Systems and Signal Processing, 2019, 137: 106355. [11] 聂雪媛, 杨国伟. 基于CFD降阶模型的阵风减缓主动控制研究[J]. 航空学报, 2015, 36(4): 1103-1111. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201504008.htmNIE X Y, YANG G W. Gust alleviation active control based on CFD reduced-order models[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1103-1111(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201504008.htm [12] 黄程德, 郑冠男, 杨国伟, 等. 基于CFD/CSD耦合含间隙三维全动舵面气动弹性研究[J]. 应用力学学报, 2018, 35(1): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201801001.htmHUANG C D, ZHENG G N, YANG G W, et al. Aeroelastic study of a three dimensional all-movable wing with free play using CFD/CSD coupling[J]. Chinese Journal of Applied Mechanics, 2018, 35(1): 1-7(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201801001.htm [13] KWON W H, PEARSON A E. Feedback stabilization of linear systems with delayed control[J]. IEEE Transactions on Automatic Control, 1980, 25(2): 266-269. doi: 10.1109/TAC.1980.1102288 [14] CAI G P, HUANG J Z. Instantaneous optimal method for vibration control of linear sampled-data systems with time delay in control[J]. Journal of Sound and Vibration, 2003, 262(5): 1057-1071. doi: 10.1016/S0022-460X(02)01083-0 [15] KIM D H, LEE I. Transonic and low-supersonic aeroelastic analysis of a two-degree-of-freedom airfoil with a freeplay non-linearity[J]. Journal of Sound and Vibration, 2000, 234(5): 859-880. doi: 10.1006/jsvi.2000.2907 [16] HE S, YANG Z C, GU Y S. Nonlinear dynamics of an aeroelastic airfoil with free-play in transonic flow[J]. Nonlinear Dynamics, 2017, 87(4): 2099-2125. doi: 10.1007/s11071-016-3176-4 -
下载:
点击查看大图
计量
- 文章访问数: 553
- HTML全文浏览量: 163
- PDF下载量: 177
- 被引次数: 0
