环量控制翼型非定常气动力建模

雷玉昌; 张登成; 张艳华

doi:10.13700/j.bh.1001-5965.2020.0360

环量控制翼型非定常气动力建模

doi: 10.13700/j.bh.1001-5965.2020.0360

雷玉昌^{1, 2},
张登成^3, ,,
张艳华³

1.
空军工程大学研究生院, 西安 710051
2.
中国人民解放军 95034部队, 百色 533600
3.
空军工程大学航空工程学院, 西安 710038

详细信息

通讯作者:
张登成, E-mail: dengcheng_zhang@163.com

中图分类号: V212.1;V211.3
计量
- 文章访问数: 558
- HTML全文浏览量: 158
- PDF下载量: 126
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-24
- 录用日期: 2020-12-21
- 网络出版日期: 2021-10-20

Unsteady aerodynamic modeling of circulation control airfoil

1.
Graduatee School, Air Force Engineering University, Xi'an 710051, China
2.
The No. 95034th Troop of People's Liberation Army, Baise 533600, China
3.
Aeronautics Engineering College, Air Force Engineering University, Xi'an 710038, China

More Information

Corresponding author: ZHANG Dengcheng, E-mail: dengcheng_zhang@163.com

摘要

摘要:
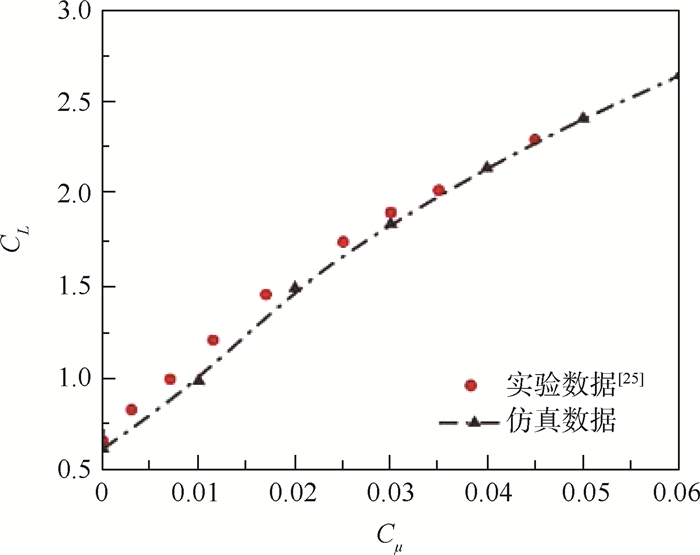
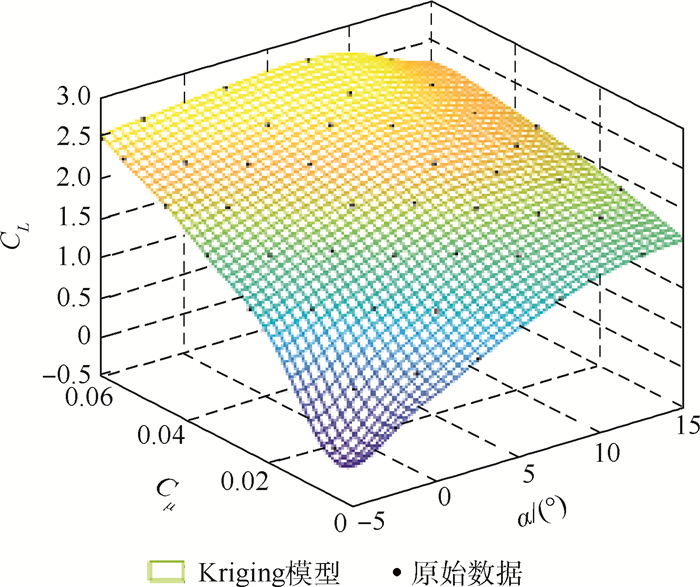
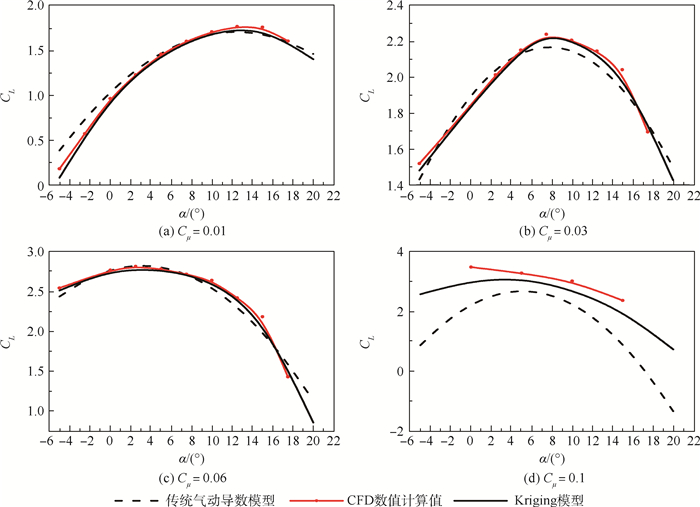
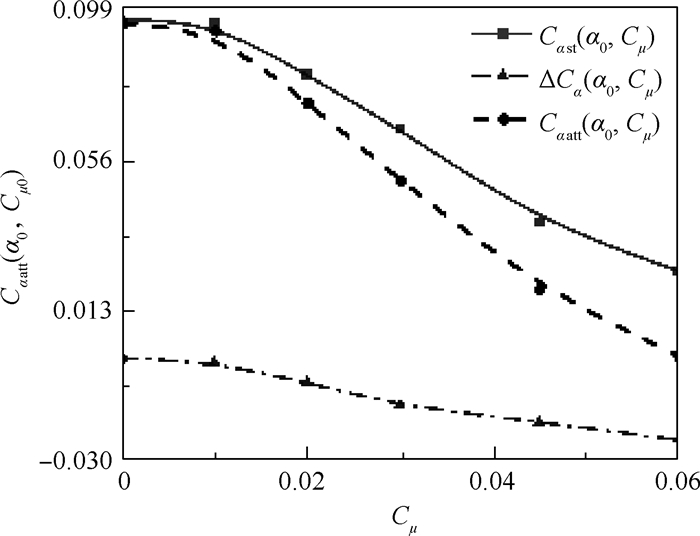
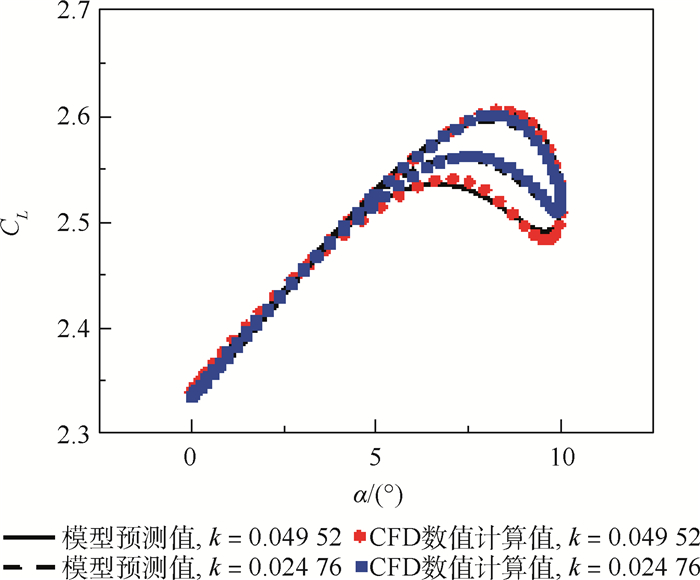
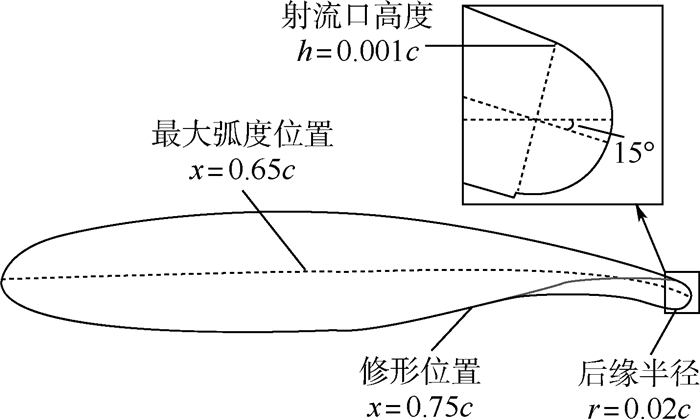
针对目前环量控制技术中射流参数与迎角对翼型气动特性的影响高度耦合，对应非定常气动力模型精度较差的研究现状，基于环量控制翼型强迫俯仰振动数值模拟数据，借助Kriging模型实现环量控制翼型的定常气动力插值，借助微分方程模型完成了适用于环量控制翼型的线性微分方程建模，采用两步线性回归参数辨识方法辨识线性微分方程模型中特征时间常数等参数，对高动量系数大振幅流动状态下的非线性影响进行修正。研究结果表明：基于Kriging模型实现的环量控制翼型定常气动力插值精度较传统气动导数模型高，建立的环量控制翼型非定常气动力模型能够精确预测不同流动状态下的气动力和力矩系数变化情况。
- 环量控制 /
- 非定常气动力 /
- 翼型 /
- 数值模拟 /
- 气动力模型 /
- 参数辨识
Abstract:
In view of the high coupling of the effects of jet parameters and angle of attack on the aerodynamic characteristics of airfoils in current circulation control technology, the accuracy of the corresponding unsteady aerodynamic models is poor. Based on the numerical simulation data of forced pitching vibration of circulation control airfoils, the steady aerodynamic interpolation of the airfoils is realized with the help of Kriging model. With the help of differential equation model, the linear differential equation modeling suitable for circulation control airfoil is completed, and the characteristic time constant and other parameters in linear differential equation models are identified by two-step linear regression parameter identification method. The nonlinear influence of high momentum coefficient and large amplitude flow is modified. The results show that the steady aerodynamic interpolation accuracy of the circulation control airfoil based on the Kriging model is higher than that of the traditional aerodynamic derivative model. The unsteady aerodynamic model can accurately predict the changes of aerodynamic force and torque coefficient under different flow conditions.
- circulation control /
- unsteady aerodynamic force /
- airfoil /
- numerical simulation /
- aerodynamic model /
- parameter identification

HTML全文

图 1 修形后的超临界翼型

Figure 1. Supercritical airfoil after modification

下载: 全尺寸图片幻灯片

图 2 翼型计算网格

Figure 2. Airfoil's computational grid

下载: 全尺寸图片幻灯片

图 3 NACA0012翼型非定常升力系数仿真与实验对比

Figure 3. Comparison of simulation and experimental results of unsteady lift coefficient of NACA0012 airfoil

下载: 全尺寸图片幻灯片

图 4 环量控制翼型升力系数仿真与实验对比

Figure 4. Comparison of simulation and experimental results of circulation control airfoil's lift coefficient

下载: 全尺寸图片幻灯片

图 5 Kriging模型预测结果

Figure 5. Prediction result of Kriging model

下载: 全尺寸图片幻灯片

图 6 Kriging模型预测误差

Figure 6. Prediction error of Kriging model

下载: 全尺寸图片幻灯片

图 7 Kriging模型与传统气动导数模型对比结果

Figure 7. Comparison between Kriging model and aerodynamic derivative model

下载: 全尺寸图片幻灯片

图 8 不同迎角、减缩频率下的同相/异相导数

Figure 8. In-phase and out-phase derivatives at different angles of attack and reduced frequencies

下载: 全尺寸图片幻灯片

图 9 时间常数随动量系数的变化曲线

Figure 9. Variation curve of time constant with momentum coefficient

下载: 全尺寸图片幻灯片

图 10 C_αatt(α₀, C_μ0)的辨识结果

Figure 10. Identification results of C_αatt(α₀, C_μ0)

下载: 全尺寸图片幻灯片

图 11 小振幅流动状态下结果对比

Figure 11. Comparison of results under small-amplitude flow

下载: 全尺寸图片幻灯片

图 12 大振幅流动状态下结果对比

Figure 12. Comparison of results under large-amplitude flow

下载: 全尺寸图片幻灯片

图 13 k_i(α, C_μ)辨识结果

Figure 13. Identification result of k_i(α, C_μ)

下载: 全尺寸图片幻灯片

图 14 非线性非定常气动力模型结果对比(C_μ=0.05)

Figure 14. Comparison of results of nonlinear unsteady aerodynamic models (C_μ=0.05)

下载: 全尺寸图片幻灯片

参考文献(30)

[1]	SHI Z W, ZHU J C, DAI X X, et al. Aerodynamic characteristics and flight testing of a UAV without control surfaces based on circulation control[J]. Journal of Aerospace Engineering, 2019, 32(1): 04018134. doi: 10.1061/(ASCE)AS.1943-5525.0000947
[2]	KANISTRAS K, VALAVANIS K P, RUTHERFORD M J. Foundations of circulation control based small-scale unmanned aircraft[M]. Berlin: Springer International Publishing, 2018: 37-46.
[3]	ENGLAR R J. Circulation control for high lift and drag generation on a STOL aircraft[J]. Journal of Aircraft, 1975, 12(5): 457-463. doi: 10.2514/3.59824
[4]	JOLSLIN R D, JONES G S. Application of circulation control technology (Progress in astronautics and aeronautics)[M]. Reston: AIAA, 2006: 105-113.
[5]	YAROS S F, SEXSTONE M G, HUEBNER L D, et al. Synergistic airframe-propulsion interactions and integrations[M]. Washington, D.C. : NASA, 1998: 14-28.
[6]	JONES G S, LIN J C, ALLEN B G, et al. Overview of CFD validation experiments for circulation control applications at NASA[C]//International Powered Lift Conference. London: Royal Aeronautical Society, 2008: 22-24.
[7]	ENGLAR R J, HUSON G G. Development of advanced circulation control wing high-lift airfoils[J]. Journal of Aircraft, 1984, 21(7): 476-483. doi: 10.2514/3.44996
[8]	ENGLAR R J. Circulation control pneumatic aerodynamics: Blown force and moment augmentation and modification-Past, present and future[C]//Fluids 2000 Conference and Exhibit, 2000: 2541.
[9]	XU H Y, QIAO C L, YANG H Q, et al. Active circulation control on the blunt trailing edge wind turbine airfoil[J]. AIAA Journal, 2018, 56(2): 554-570. doi: 10.2514/1.J056223
[10]	REGER R, NICKELS A, UKEILEY L, et al. On the acoustics of a circulation control airfoil[J]. Journal of Sound and Vibration, 2017, 388: 85-104. doi: 10.1016/j.jsv.2016.10.015
[11]	WARSOP C, CROWTHER W J. Fluidic flow control effectors for flight control[J]. AIAA Journal, 2018, 56(10): 3808-3824. doi: 10.2514/1.J056787
[12]	WARSOP C, CROWTHER W. NATO AVT-239 task group: Flight demonstration of fluidic flight controls on the MAGMA subscale demonstrator aircraft[C]//AIAA Scitech 2019 Forum. Reston: AIAA, 2019.
[13]	汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报, 2016, 37(8): 2331-2347. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201608001.htm WANG Q, QIAN W Q, DING D. A review of unsteady aerodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201608001.htm
[14]	孙海生, 张海酉, 刘志涛. 大迎角非定常气动力建模方法研究[J]. 空气动力学学报, 2011, 29(6): 733-737. doi: 10.3969/j.issn.0258-1825.2011.06.008 SUN H S, ZHANG H Y, LIU Z T. Comparative evaluation of unsteady aerodynamics modeling approaches at high angle of attack[J]. Acta Aerodynamica Sinica, 2011, 29(6): 733-737(in Chinese). doi: 10.3969/j.issn.0258-1825.2011.06.008
[15]	LOTH J L, BOASSON M. Circulation controlled STOL wing optimization[J]. Journal of Aircraft, 1984, 21(2): 128-134. doi: 10.2514/3.48235
[16]	ENGLAR R J, SMITH M J, KELLEY S M, et al. Application of circulation control to advanced subsonic transport aircraft, Part Ⅰ-Airfoil development[J]. Journal of Aircraft, 1994, 31(5): 1160-1168. doi: 10.2514/3.56907
[17]	HOHOLIS G A. Assessment of fluidic control effectors using computational fluid dynamics[D]. Liverpool: University of Liverpool, 2016: 1-30.
[18]	KRUKOW I, DINKLER D. A reduced-order model for the investigation of the aeroelasticity of circulation-controlled wings[J]. CEAS Aeronautical Journal, 2014, 5(2): 145-156. doi: 10.1007/s13272-013-0097-5
[19]	SEMAAN R, EL SAYED M Y, RADESPIEL R. Sparse model of the lift gains of a circulation control wing with unsteady coanda blowing[M]. Berlin: Springer, 2019: 3-18.
[20]	LIN G F, LAN C, BRANDON J, et al. A generalized dynamic aerodynamic coefficient model for flight dynamics applications[C]//22nd Atmospheric Flight Mechanics Conference. Reston: AIAA, 1997: 3643.
[21]	GOMAN M, KHRABROV A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack[J]. Journal of Aircraft, 1994, 31(5): 1109-1115. doi: 10.2514/3.46618
[22]	汪清, 蔡金狮. 飞机大攻角非定常气动力建模与辨识[J]. 航空学报, 1996, 17(4): 391-398. doi: 10.3321/j.issn:1000-6893.1996.04.003 WANG Q, CAI J S. Unsteady aerodynamic modeling and identification of airplane at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 1996, 17(4): 391-398(in Chinese). doi: 10.3321/j.issn:1000-6893.1996.04.003
[23]	孔轶男, 王立新, 何开锋, 等. 过失速机动的模糊逻辑建模仿真[J]. 北京航空航天大学学报, 2007, 33(10): 1174-1177. doi: 10.3969/j.issn.1001-5965.2007.10.011 KONG Y N, WANG L X, HE K F, et al. Fuzzy logic models for unsteady post stall maneuver[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(10): 1174-1177(in Chinese). doi: 10.3969/j.issn.1001-5965.2007.10.011
[24]	付军泉, 史志伟, 陈坤, 等. 基于EKF的实时循环神经网络在非定常气动力建模中的应用[J]. 空气动力学学报, 2018, 36(4): 658-663. doi: 10.7638/kqdlxxb-2016.0131 FU J Q, SHI Z W, CHEN K, et al. Applications of real-time recurrent neural network based on extended Kalman filter in unsteady aerodynamics modeling[J]. Acta Aerodynamica Sinica, 2018, 36(4): 658-663(in Chinese). doi: 10.7638/kqdlxxb-2016.0131
[25]	JONES G. Pneumatic flap performance for a 2D circulation control airfoil, stedy and pulsed[R]. Washington, D.C. : Langley Research Center, 2005: 191-244.
[26]	KHARATI KOOPAEE M. Effect of flow regime change from subsonic to transonic on the air loads of an oscillating airfoil[J]. Journal of Fluids and Structures, 2014, 50: 312-328. doi: 10.1016/j.jfluidstructs.2014.05.017
[27]	韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201611001.htm HAN Z H. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201611001.htm
[28]	龚正, 沈宏良. 非定常气动力非线性微分方程建模方法[J]. 航空学报, 2011, 32(1): 83-90. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201101011.htm GONG Z, SHEN H L. Unsteady aerodynamic modeling method using nonlinear differential equations[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 83-90(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201101011.htm
[29]	雷玉昌, 张登成, 张艳华, 等. 超临界翼型的双射流环量控制研究[J]. 飞行力学, 2020, 38(4): 16-21. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX202004004.htm LEI Y C, ZHANG D C, ZHANG Y H, et al. Circulation control of double jet flow on supercritical airfoil[J]. Flight Dynamics, 2020, 38(4): 16-21(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX202004004.htm
[30]	GREENWELL D, KHRABROV A, GOMAN M, et al. Two-step linear regression method for identification of high incidence unsteady aerodynamic model[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston: AIAA, 2001: 4080.