函数传递法求解悬链线问题

马艳红; 时成龙; 洪杰; 李超

doi:10.13700/j.bh.1001-5965.2020.0367

函数传递法求解悬链线问题

doi: 10.13700/j.bh.1001-5965.2020.0367

马艳红^{1, 2, ,},
时成龙¹,
洪杰^{1, 2},
李超¹

1.
北京航空航天大学能源与动力工程学院, 北京 100083
2.
先进航空发动机协同创新中心, 北京 100083

详细信息

通讯作者:
马艳红, E-mail: mayanhong@buaa.edu.cn

中图分类号: V239
计量
- 文章访问数: 713
- HTML全文浏览量: 152
- PDF下载量: 133
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-29
- 录用日期: 2020-09-11
- 网络出版日期: 2021-10-20

Solving catenary problem using function transfer method

MA Yanhong^{1, 2
, ,},
SHI Chenglong¹,
HONG Jie^{1, 2},
LI Chao¹

1.
School of Energy and Power Engineering, Beihang University, Beijing 100083, China
2.
Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100083, China

More Information

Corresponding author: MA Yanhong, E-mail: mayanhong@buaa.edu.cn

摘要

摘要:
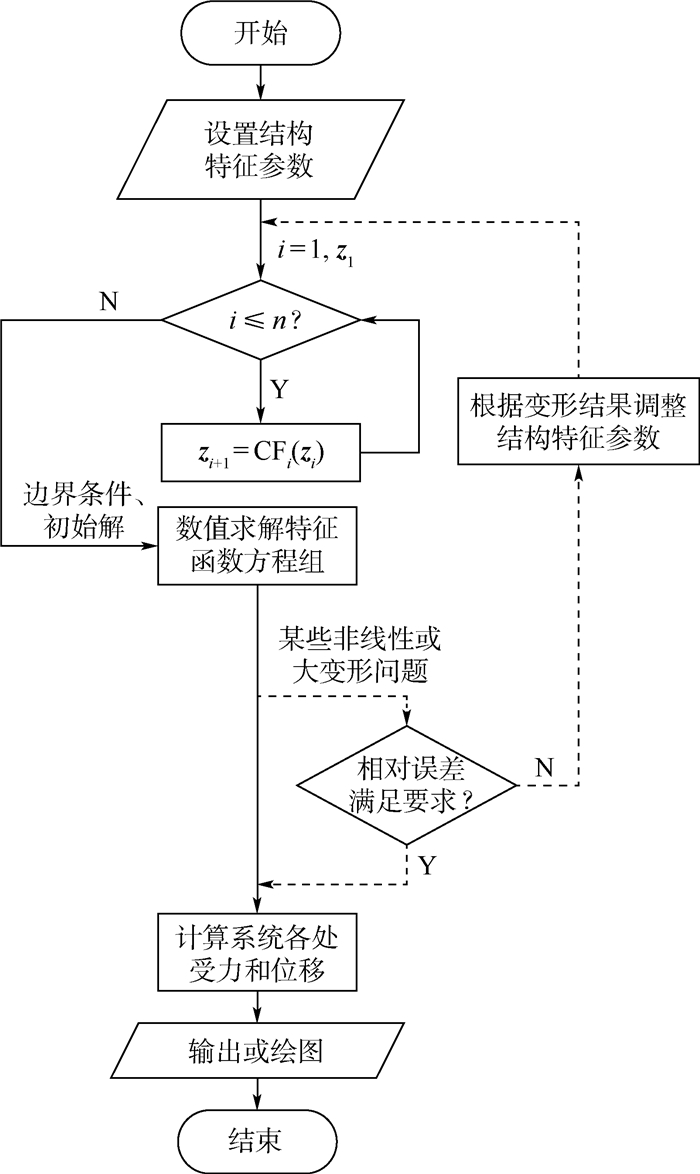
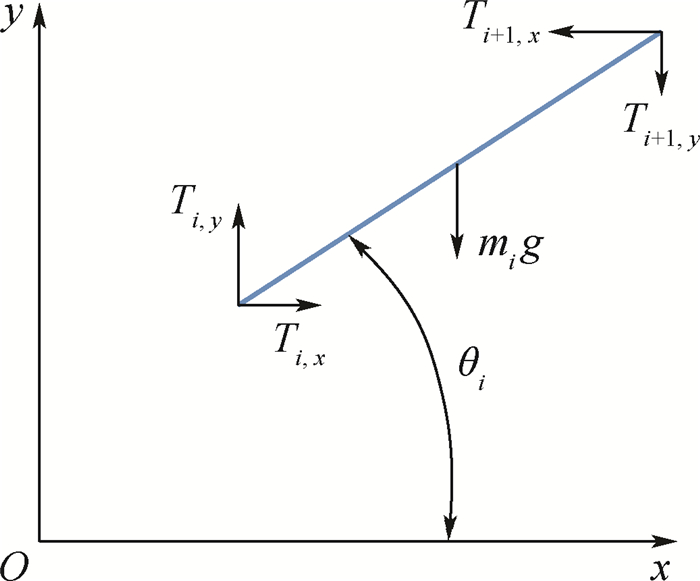
悬链线问题是一类经典又多变的力学问题，其曲线构形指导着桥梁等工程应用的结构设计。为了求得结构特征或载荷特征不同的悬链线的变形，提出了一种基于传递矩阵法思想的、通用性较好的求解方法。首先，提炼出悬链力学模型，将悬链顺序划分成若干简单单元，结合单元力平衡和本构-几何关系解得单元特征函数方程组，顺序嵌套单元特征函数方程组获得整体特征函数方程组；然后，使用离散Newton迭代法对该非线性方程组进行求解，获得悬链的受力和变形；最后，算例验证了结果与解析解的一致性。函数传递法对具有复杂结构特征和载荷特征的悬链线问题有很好的适用性，对求解其他可划分为若干首尾相接结构单元的结构系统的广义变形也适用。
- 函数传递法 /
- 传递矩阵法 /
- 悬链线 /
- Newton迭代法 /
- 广义变形
Abstract:
Catenary problem is a kind of classical and changeable mechanical problem, whose curve configuration guides the structural design of engineering applications such as bridge. In order to obtain the deformation of catenary with different structural or load characteristics, a general method based on transfer matrix method is proposed. The catenary mechanics model is extracted, and the catenary is divided sequentially into several simple elements. The characteristic function group of element state parameters is obtained by combining element force balance and constitutive-geometry relationship. The whole characteristic function group is obtained by nesting element characteristic function group sequentially. Then the discrete Newton iterative method is used to solve the equations of nonlinear whole characteristic function group, and finally the forces and deformation of catenary are obtained. An example showed that the results were consistent with the analytical solution. The function transfer method is applicable to the catenary problems with complex structural characteristics and load characteristics, and also applicable to solving the generalized deformation of other structural systems which can be divided into several head-to-tail structural elements.
- function transfer method /
- transfer matrix method /
- catenary /
- Newton iterative method /
- generalized deformation

HTML全文

图 1 悬链结构系统力学模型

Figure 1. Mechanical model of cable chain structure system

下载: 全尺寸图片幻灯片

图 2 单元受力分析

Figure 2. Load analysis of element

下载: 全尺寸图片幻灯片

图 3 结构变形求解流程

Figure 3. Flowchart for solving structure deformation

下载: 全尺寸图片幻灯片

图 4 刚体杆件单元受力分析

Figure 4. Load analysis of rigid rod element

下载: 全尺寸图片幻灯片

图 5 悬链线解析解与数值解曲线

Figure 5. Analysis and numerical solution curves of catenary

下载: 全尺寸图片幻灯片

图 6 两组悬链线解

Figure 6. Two groups of catenary solutions

下载: 全尺寸图片幻灯片

图 7 不同跨长比的悬链线

Figure 7. Catenary with different span/length ratios

下载: 全尺寸图片幻灯片

图 8 悬链线构形参数间的变化关系

Figure 8. Relationship between configuration parameters of catenary

下载: 全尺寸图片幻灯片

图 9 经典悬链线解与附加重物悬链线解

Figure 9. Classical catenary solution and catenary with additional weight

下载: 全尺寸图片幻灯片

图 10 经典悬链线解与带弹性悬链线解

Figure 10. Classical catenary solution and catenary with elasticity

下载: 全尺寸图片幻灯片

图 11 经典悬链线与悬索桥曲线

Figure 11. Classical catenary and suspension bridge curve

下载: 全尺寸图片幻灯片

图 12 经典悬链线与跳绳曲线

Figure 12. Classical catenary and rope skipping curve

下载: 全尺寸图片幻灯片

表 1 常见边界条件参数

Table 1. Common boundary condition parameters

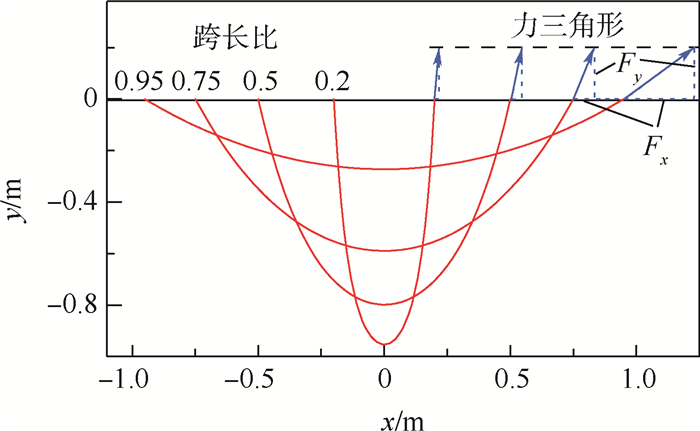
边界条件	挠度	挠角	弯矩	剪力
简支	0	θ_x	0	F_x
自由	y_x	θ_x	0	0
弹性支承	y_x	θ_x	0	K_springy_x

下载: 导出CSV

表 2 悬链算例参数

Table 2. Example parameters of catenary

参数	数值
跨度L_span/m	1.5
索链总长L_line/m	2.0
横截面圆半径R_line/m	1.0×10^-3
材料密度ρ/(kg·m^-3)	7 800

下载: 导出CSV

表 3 悬链算例结果

Table 3. Example results of catenary

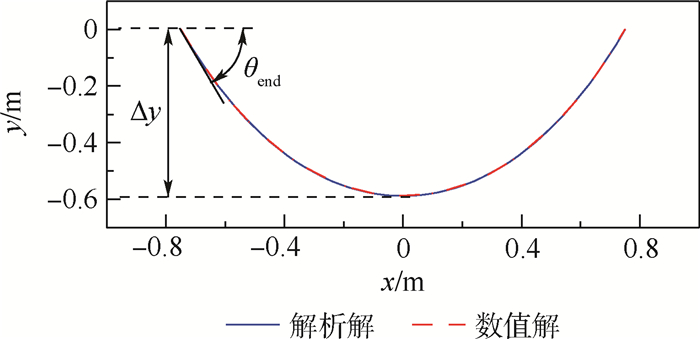
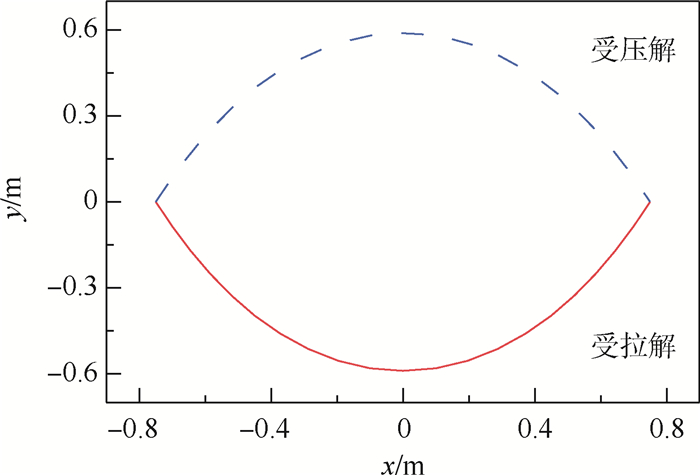
解析/数值解	高低差Δy/m	索端水平拉力F_x-end/N	索端角θ_end/(°)
解析解	0.588 6	0.0137 8	60.96
数值解	0.589 5	0.0135 9	59.72
相对误差/%	0.15	-1.4	-2.0

下载: 导出CSV

参考文献(18)

[1]	ROUTH E J. A treatise on analytical statics: With numerous examples[M]. Cambridge: Cambridge University Press, 2013.
[2]	周强, 杨文兵, 杨新华. 斜拉桥索力调整在ANSYS中的实现[J]. 华中科技大学学报(城市科学版), 2005, 22(增刊): 81-83. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCJ2005S1023.htm ZHOU Q, YANG W B, YANG X H. Simulation of tensing stayed cables in ANSYS[J]. Journal of Huazhong University of Science and Technology (Urban Science Edition), 2005, 22(Supplement): 81-83(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-WHCJ2005S1023.htm
[3]	THAI H T, KIM S E. Nonlinear static and dynamic analysis of cable structures[J]. Finite Elements in Analysis and Design, 2011, 47(3): 237-246. doi: 10.1016/j.finel.2010.10.005
[4]	JAYARAMAN H B, KNUDSON W C. A curved element for the analysis of cable structures[J]. Computers and Structures, 1981, 14(3-4): 325-333. doi: 10.1016/0045-7949(81)90016-X
[5]	郑平芳. 有限元中索单元的研究及应用进展[J]. 山西建筑, 2011, 37(28): 42-43. https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX201128026.htm ZHENG P F. Research on cable element in finite element and its application progress[J]. Shanxi Architecture, 2011, 37(28): 42-43(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX201128026.htm
[6]	PESTEL E, LECKIE F. Matrix methods in elastomechanics[M]. New York: McGraw-Hill Book Company, 1963.
[7]	RUBIN S. Transmission matrices for vibration and their relation to admittance and impedance[J]. Journal of Manufacturing Science and Engineering, 1964, 86(1): 9-21.
[8]	顾家柳, 丁奎元, 刘启洲, 等. 转子动力学[M]. 北京: 国防工业出版社, 1985. GU J L, DING K Y, LIU Q Z, et al. Rotordynamics[M]. Beijing: National Defense Industry Press, 1985(in Chinese).
[9]	夏林林, 吴开腾. 大范围求解非线性方程组的指数同伦法[J]. 计算数学, 2014, 36(2): 215-224. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSX201402008.htm XIA L L, WU K T. An exponential homotopy method for nonlinear equations in large scope[J]. Mathematica Numerica Sinica, 2014, 36(2): 215-224(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSSX201402008.htm
[10]	夏林林, 户晗蕾, 吴开腾. 非线性方程组数值方法的研究进展[J]. 内江师范学院学报, 2013, 28(10): 12-17. https://www.cnki.com.cn/Article/CJFDTOTAL-NJSG201310004.htm XIA L L, HU H L, WU K T. Progress in the research of nonliear equations via numerical methods[J]. Journal of Neijiang Normal University, 2013, 28(10): 12-17(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-NJSG201310004.htm
[11]	颜庆津. 数值分析[M]. 3版. 北京: 北京航空航天大学出版社, 2006. YAN Q J. Numerical analysis[M]. 3rd ed. Beijing: Beihang University Press, 2006(in Chinese).
[12]	TAIPING H. The transfer matrix impedance coupling method for the eigensolutions of multi-spool rotor systems[J]. Journal of Vibration and Acoustics, 1988, 110(4): 468-472. doi: 10.1115/1.3269552
[13]	LEE J W, LEE J Y. An exact transfer matrix expression for bending vibration analysis of a rotating tapered beam[J]. Applied Mathematical Modelling, 2018, 53: 167-188. doi: 10.1016/j.apm.2017.08.022
[14]	ROSEN A, GUR O. A transfer matrix model of large deformations of curved rods[J]. Computers and Structures, 2018, 87(7-8): 467-484.
[15]	王建国, 逄焕平, 李雪峰. 悬索桥线形分析的悬链线单元法[J]. 应用力学学报, 2008, 25(4): 627-631. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX200804018.htm WANG J G, PANG H P, LI X F. Catenary cable element method for cable curve or suspension bridges[J]. Chinese Journal of Applied Mechanics, 2008, 25(4): 627-631(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX200804018.htm
[16]	何竞飞. 跳绳曲线的数值解及误差估计的间接判定法[J]. 中南工业大学学报, 1995, 26(4): 532-535. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD504.024.htm HE J F. The numerical solution of rope skipping curve and the indirect evaluation of its error[J]. Journal of Central South University of Technology, 1995, 26(4): 532-535(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD504.024.htm
[17]	王庸禄. 对跳绳式捻股成绳机转子弓外形设计及钢丝(股)张力控制的探讨[J]. 金属制品, 1985(6): 8-17. https://www.cnki.com.cn/Article/CJFDTOTAL-JSZP198506001.htm WANG Y L. Discussion on shape design of rotor bow and tension control of steel wire (strand) of rope skipping stranding machine[J]. Metal Products, 1985(6): 8-17(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSZP198506001.htm
[18]	罗雯瑛. 有限到无限: 基于离散静力平衡推导悬链线方程和梁位移方程[J]. 力学与实践, 2020, 42(1): 85-91. https://www.cnki.com.cn/Article/CJFDTOTAL-LXYS202001015.htm LUO W Y. From finiteness to infinity: Deriving the catenary equation and the beam displacement equation based on the discrete static equilibrium model[J]. Mechanics in Engineering, 2020, 42(1): 85-91(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-LXYS202001015.htm