疲劳统计学智能化中的高镇同法

徐家进

doi:10.13700/j.bh.1001-5965.2020.0373

疲劳统计学智能化中的高镇同法

doi: 10.13700/j.bh.1001-5965.2020.0373

徐家进^,

力中国际融资租赁有限公司, 广州 510620

详细信息

通讯作者:
徐家进, E-mail: xujiajin666@163.com

中图分类号: O212.1
计量
- 文章访问数: 780
- HTML全文浏览量: 234
- PDF下载量: 67
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-30
- 录用日期: 2020-11-27
- 网络出版日期: 2021-10-20

Gao Zhentong method in intelligentization of statistics in fatigue

XU Jiajin^,

L & Z International Leasing Co. Ltd., Guangzhou 510620, China

More Information

Corresponding author: XU Jiajin, E-mail: xujiajin666@163.com

摘要

摘要:
在疲劳统计学中威布尔分布起着非常重要的作用，但3个参数的威布尔分布在数学形式上比较复杂。通过样本数据估计这3个参数，可通过威布尔概率坐标纸，但其使用不便，且误差较大；也可通过解析法，求解3个联立的超越方程组，但存在不自冾的问题。为此，提出了智能化解决方案——高镇同法，高镇同法充分利用了Python的特点，能够方便地同时给出威布尔分布的3个参数，为威布尔分布的理论研究、实际应用和疲劳统计学的智能化奠定了坚实的基础。
- 三参数威布尔分布 /
- 安全寿命 /
- Python /
- 高镇同法 /
- 智能疲劳统计学
Abstract:
The Weibull distribution plays a very important role in statistics in fatigue, but the Weibull distribution of the three parameters is more complicated in mathematical form. The three parameters can be estimated through sample data. One is the "Weibull probability paper", but this method is inconvenient to use and the error is relatively large. The other is the "analytical method". To solve the three simultaneous transcendental equations, although it can be solved by a computer, there is still the problem of "incompatibility". To this end, an intelligent solution-Gao Zhentong method is proposed, which makes full use of the characteristics of Python and can conveniently give the three parameters of Weibull distribution at the same time. This lays a solid foundation for the theoretical research, practical application and intelligentization of statistics in fatigue of Weibull distribution.
- three-parameter Weibull distribution /
- safe life /
- Python /
- Gao Zhentong method /
- intelligent fatigue statistics

HTML全文

图 1 标准威布尔分布概率密度函数

Figure 1. Standard Weibull distribution probability density function

下载: 全尺寸图片幻灯片

图 2 正态和威布尔分布可靠度比较(例1)

Figure 2. Comparison of normal and Weibull distribution reliability (Example 1)

下载: 全尺寸图片幻灯片

图 3 正态和威布尔分布可靠度比较(例2)

Figure 3. Comparison of reliability between Normal and Weibull distribution (Example 2)

下载: 全尺寸图片幻灯片

图 4 安全寿命与相关系数的关系(例3)

Figure 4. Safety life versus correlation coefficient (Example 3)

下载: 全尺寸图片幻灯片

图 5 安全寿命与相关系数的关系(例4)

Figure 5. Safety life versus correlation coefficient (Example 4)

下载: 全尺寸图片幻灯片

图 6 安全寿命与相关系数的关系(文献[11]中的表 3)

Figure 6. Safety life versus correlation coefficient (Table 3 of Ref.[11])

下载: 全尺寸图片幻灯片

图 7 S-N拟合曲线

Figure 7. S-N curve fiting

下载: 全尺寸图片幻灯片

图 8 a-N拟合曲线

Figure 8. a-N curve fitting

下载: 全尺寸图片幻灯片

表 1 一组疲劳寿命数据^[1]

Table 1. A set of fatigue life data^[1]

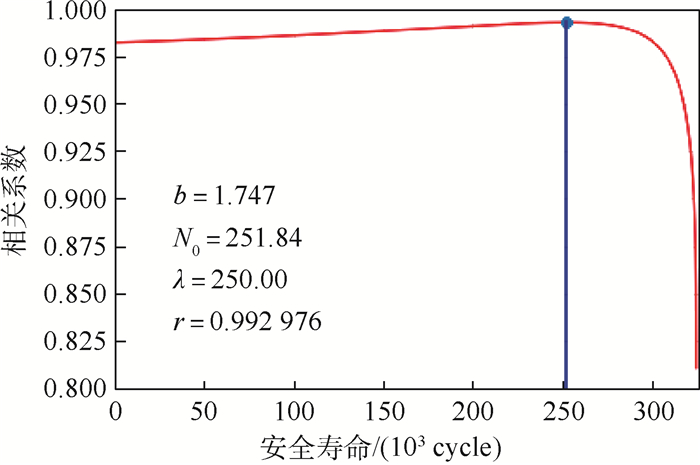
疲劳寿命/(10³ cycle)
350	380	400	430	450
470	480	500	520	540
550	570	600	610	630
650	670	730	770	840
均值N_av=557 标准差s=132.15 中值N_m=545

下载: 导出CSV

表 2 100个试件在同一应力条件下疲劳寿命数据

Table 2. Fatigue life data of 100 specimens under the same stress condition

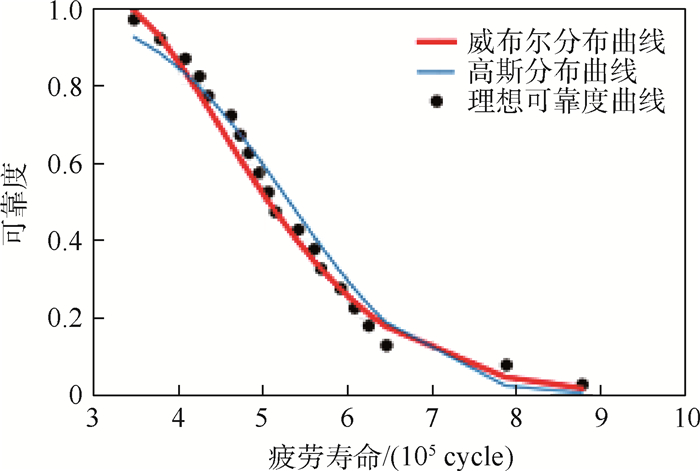
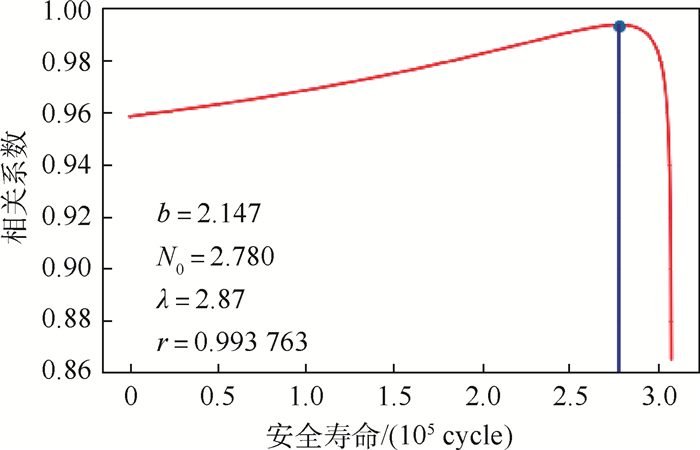
疲劳寿命/(10⁵cycle)
3.08	3.26	3.32	3.48	3.49	3.56	3.69	3.7	3.78	3.79
3.8	3.87	3.95	4.07	4.08	4.1	4.12	4.2	4.24	4.25
4.28	4.31	4.31	4.36	4.54	4.58	4.6	4.62	4.63	4.65
4.67	4.67	4.72	4.73	4.75	4.77	4.8	4.82	4.84	4.9
4.92	4.93	4.95	4.96	4.98	4.99	5.02	5.03	5.06	5.08
5.06	5.1	5.12	5.15	5.18	5.2	5.22	5.38	5.41	5.46
5.47	5.53	5.56	5.6	5.61	5.63	5.64	5.65	5.68	5.69
5.73	5.82	5.86	5.91	5.94	5.95	5.99	6.04	6.08	6.13
6.16	6.19	6.21	6.26	6.32	6.33	6.36	6.41	6.46	6.81
77.35	7.82	7.88	7.96	8.31	8.45	8.47	8.79	9.87
均值=5.315 标准差s=1.289 中值N_m=5.07

下载: 导出CSV

表 3 例6的一组数据

Table 3. Example 6 a set of data

组号	S_max/MPa	lg N
1	380	2.593 3
2	353.6	2.897 6
3	326.4	3.220 1
4	299.2	3.867 1

下载: 导出CSV

表 4 例7的一组数据

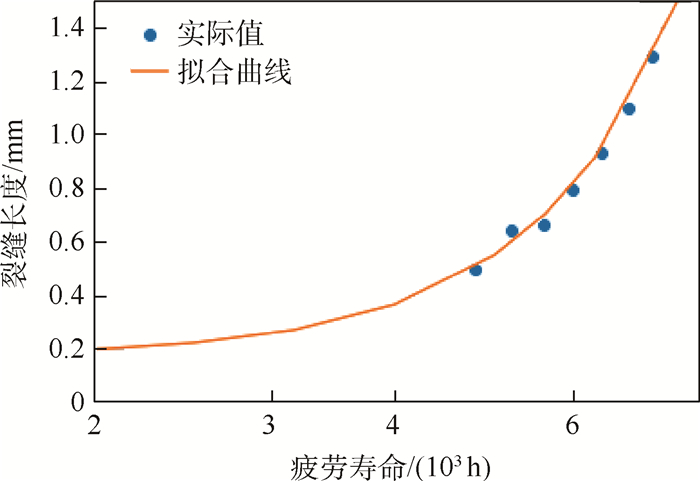
Table 4. Example 7 a set of data

组号	a/mm	N/h
1	0.497 8	4 800
2	0.642	5 200
3	0.665 5	5 600
4	0.797 6	6 000
5	0.932 2	6 400
6	1.099 8	6 800
7	1.292 9	7 200

下载: 导出CSV

参考文献(15)

[1]	高镇同. 疲劳应用统计学[M]. 北京: 国防工业出版社, 1986: 83, 136, 253. GAO Z T. Fatigue applied statistics[M]. Beijing: National Defense Industry Press, 1986: 83, 136, 253(in Chinese).
[2]	高镇同院士80华诞庆贺文集[Z]. 北京: 北京航空航天大学, 2008: 4. Academician Gao Zhentong's 80th birthday celebration collection[Z]. Beijing: Beihang University, 2008: 4(in Chinese).
[3]	如何用MATLAB求威布尔分布三个参数[EB/OL]. (2013-06-09)[2020-05-01]. http://www.cadedu.com/CADzhidao/matlab/2013-06-09/askcad40148.html. How to use MATLAB to find the three parameters of Weibull distribution[EB/OL]. (2013-06-09)[2020-05-01]. http://www.cadedu.com/CADzhidao/matlab/2013-06-09/askcad40148.html (in Chinese).
[4]	于晓红, 张来斌, 王朝晖, 等. 基于新的威布尔分布参数估计法的设备寿命可靠性分析[J]. 机械强度, 2007, 29(6): 932-936. doi: 10.3321/j.issn:1001-9669.2007.06.014 YU X H, ZHANG L B, WANG Z H, et al. Reliability life analysis of the equipment based on new Weibull distribution parameter estimation method[J]. Mechanical Strength, 2007, 29(6): 932-936(in Chinese). doi: 10.3321/j.issn:1001-9669.2007.06.014
[5]	王海涛, 陈星, 段斐翡. 三参数威布尔分布模型在系统的可靠性评估中的应用[J]. 机械与电子, 2015(7): 78-80. https://www.cnki.com.cn/Article/CJFDTOTAL-JXYD201503022.htm WANG H T, CHEN X, DUAN F F. Estimation the system reliability based on 3-parameter Weibull distribution model[J]. Machinery and Electronics, 2015(7): 78-80(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXYD201503022.htm
[6]	乔宏霞, 郭向柯, 朱彬荣. 三参数Weibull分布的多因素作用下混凝土加速寿命试验[J]. 材料导报, 2019, 33(2): 639-642. https://www.cnki.com.cn/Article/CJFDTOTAL-CLDB201904015.htm QIAO H X, GUO X K, ZHU B R. Accessibility lift test of concrete under multiple factors based on three-parameter Weibull distribution[J]. Material Reports, 2019, 33(2): 639-642(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CLDB201904015.htm
[7]	高镇同, 熊峻江. 疲劳可靠性[M]. 北京: 北京航空航天大学出版社, 2000: 86, 315-319. GAO Z T, XIONG J J. Fatigue reliability[M]. Beijing: Beihang University Press, 2000: 86, 315-319(in Chinese).
[8]	茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 2版. 北京: 高等教育出版社, 2006: 31-32. MAO S S, WANG J L, PU X L. Advanced mathematical statistics[M]. 2nd ed. Beijing: Higher Education Press, 2006: 31-32(in Chinese).
[9]	HOGG R V, MCKEAN J W, CRAI A T. 数理统计导论[M]. 7版. 北京: 机械工业出版社, 2015: 174-175. HOGG R V, MCKEAN J W, CRAIG A T. Introduction to mathematical statistics[M]. 7th ed. Beijing: Machinery Industry Press, 2015: 174-175(in Chinese).
[10]	TRIVEDI K S. 计算机应用与可靠性工程中的概率统计[M]. 2版. 北京: 电子工业出版社, 2015: 601-602. TRIVEDI K S. Probability and statistics with reliability, queuing, and computer science applications[M]. 2nd ed. Beijing: Electronic Industry Press, 2015: 601-602(in Chinese).
[11]	傅惠民, 高镇同. 确定威布尔分布三参数的相关系数优化法[J]. 航空学报, 1990, 11(7): 323-327. doi: 10.3321/j.issn:1000-6893.1990.07.003 FU H M, GAO Z T. An optimization method of correlation coefficient for determining a three-parameters Weibull distribution[J]. Acta Aeronautica et Astronautic Sinica, 1990, 11(7): 323-327(in Chinese). doi: 10.3321/j.issn:1000-6893.1990.07.003
[12]	吴立言, 刘更, 王步瀛. 可靠性分析的三参数法[J]. 航空学报, 1995, 16(3): 376-380. doi: 10.3321/j.issn:1000-6893.1995.03.029 WU L Y, LIU G, WANG B Y. Three-moment method for reliability analysis[J]. Acta Aeronautic et Astronautic Sinica, 1995, 16(3): 376-380(in Chinese). doi: 10.3321/j.issn:1000-6893.1995.03.029
[13]	胡恩平, 罗兴柏, 刘国庆. 三参数Weibull分布几种常用的参数估计方法[J]. 沈阳工业学院学报, 2000, 19(3): 89-93. https://www.cnki.com.cn/Article/CJFDTOTAL-SGXY200003018.htm HU E P, LUO X B, LIU G Q. Parameter estimating methods for the three parameters Weibull distribution[J]. Journal of Shen-yang Institute of Technology, 2000, 19(3): 89-93(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SGXY200003018.htm
[14]	徐远龙, 徐人平. 产品寿命分布分析和可靠度估计[J]. 机电产品开发与创新, 2007, 20(6): 74-76. https://www.cnki.com.cn/Article/CJFDTOTAL-JDCP200706032.htm XU Y L, XU R P. Lifetime distribution analysis and reliability estimation of production[J]. Development & Innovation of Machinery & Electrical Products, 2007, 20(6): 74-76(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JDCP200706032.htm
[15]	赵冰锋, 吴素君. 三参数威布尔分布参数估计方法[J]. 金属热处理, 2007, 32: 443-446. doi: 10.3969/j.issn.0254-6051.2007.z1.118 ZHAO B F, WU S J. Parameter estimation method for 3-parameter Weibull distribution[J]. Metal Heat Treatment, 2007, 32: 443-446(in Chinese). doi: 10.3969/j.issn.0254-6051.2007.z1.118