-
摘要:
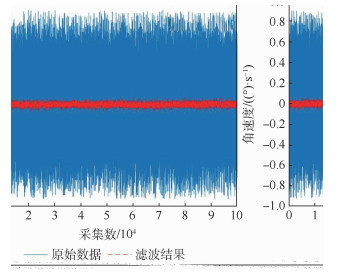
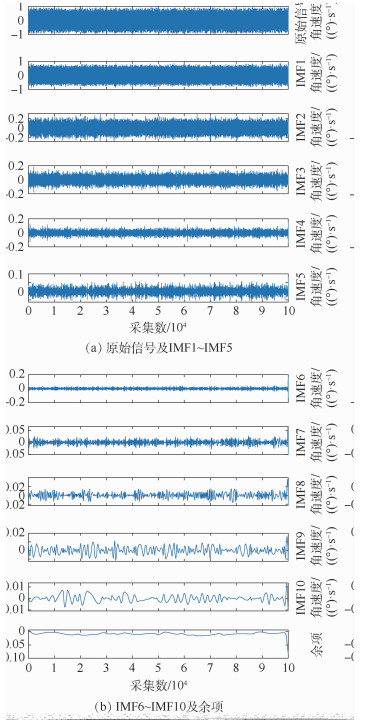
为了抑制微机械电子系统（MEMS）陀螺仪的随机漂移，基于经验模态分解（EMD）和模态集合选择标准，结合时间序列建模滤波法，提出了一种改进的MEMS陀螺仪随机漂移分析方法。首先，通过EMD将MEMS陀螺仪原始数据分解为多个本征模态函数（IMF），利用模态集合选择标准将IMF分为噪声IMF、噪声与信号混合IMF和信号IMF三类；然后，对混合IMF进行重构、时间序列建模及自适应卡尔曼滤波（AKF）；最后，将3类信号重构，实现MEMS陀螺仪信号去噪。实验表明：所提方法有更好的去噪效果和实时性，提高了MEMS陀螺仪的使用精度。
-
关键词:
- 微机械电子系统(MEMS)陀螺仪 /
- 自适应卡尔曼滤波(AKF) /
- 时间序列模型 /
- Allan方差 /
- 经验模态分解(EMD)
Abstract:In order to reduce the random drift of Micro-Electro-Mechanical System (MEMS) gyroscope, an improved random drift analysis method of MEMS gyroscope is proposed, based on an improved Empirical Mode Decomposition (EMD) and a mode set selection criterion, combined with the method of time series model and filter. The original data of MEMS gyroscope was decomposed into several Intrinsic Mode Functions (IMFs) by EMD, and IMFs were divided into noise IMFs, mixed IMFs and signal IMFs by using the mode set selection criterion. The mixed IMFs were reconstructed, the time series model of the mixed IMFs after reconstruction was formulated, and Adaptive Kalman Filter (AKF) after modeling was finished. The denoised signal is obtained by reconstruction of three types of signal. Experimental result shows that the proposed method has better denoising effect and real-time performance, which greatly improves the using precision of MEMS gyroscope.
-
表 1 相关程度判断标准
Table 1. Judgment criteria of correlation degree
相关系数 相关程度 0.8~1.0 极强相关 0.6~0.8 强相关 0.4~0.6 中度相关 0.2~0.4 弱相关 0~0.2 极弱相关或无相关 
下载: 导出CSV
表 2 各阶IMF分量的相关系数值
Table 2. Correlation coefficient of each order of IMF
IMF 相关系数 IMF 相关系数 1 0.961 8 6 0.011 4 2 0.256 8 7 0.006 4 3 0.077 8 8 0.003 8 4 0.032 2 9 0.002 5 5 0.014 5 10 0.002 9
下载: 导出CSV
表 3 各阶IMF自相关函数方差
Table 3. Variance of autocorrelation function of each order of IMF
IMF 方差 IMF 方差 1 3.13×10-5 6 4.82×10-4 2 2.72×10-5 7 0.001 0 3 5.20×10-5 8 0.001 9 4 1.09×10-4 9 0.004 5 5 2.24×10-4 10 0.006 1
下载: 导出CSV
表 4 AR模型系数
Table 4. Coefficientof AR model
模型 a1 a2 a3 FPE AIC AR(1) -0.935 1 0 0 3.693 6×10-4 -5.065 9×105 AR(2) -1.750 0 0.870 8 0 8.927 3×10-5 -6.485 9×105 AR(3) -2.353 0 2.083 3 -0.692 0 4.644 4×10-5 -7.139 4×105
下载: 导出CSV
表 5 Allan方差误差项对比分析
Table 5. Comparison analysis on Allan variance error terms
原始数据和方法 量化噪声/(°) 角度随机游走/ ((°)·h 
零偏不稳定性/ ((°)·h-1) 角速率游走/ ((°)·h 
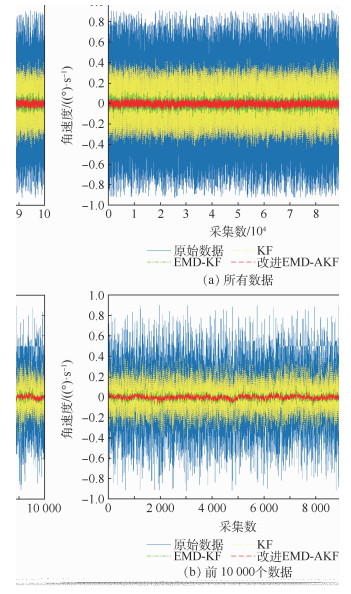
速率斜坡/ ((°)·h-2) 原始数据 77.996 1 1.371 4 95.828 5 261.649 9 203.768 0 KF 26.262 5 1.394 9 36.813 8 100.523 7 78.284 4 EMD-KF 6.527 1 0.577 5 46.413 7 122.321 9 94.460 9 改进EMD-AKF 3.422 5 0.302 7 29.132 0 71.074 3 53.691 5
下载: 导出CSV
-
[1] 沈强, 刘洁瑜, 赵乾, 等. MEMS陀螺阵列的RCC-OBE估计融合方法[J]. 北京航空航天大学学报, 2018, 44(11): 2373-2379. doi: 10.13700/j.bh.1001-5965.2018.0091SHEN Q, LIU J Y, ZHAO Q, et al. RCC-OBE estimation fusion approach for MEMS gyro array[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(11): 2373-2379(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0091 [2] 田方澍. 基于多传感器的多旋翼无人机导航解算方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017: 38-55.TIAN F S. Research on navigation solution of multi-rotor UAV based on multiple sensors[D]. Harbin: Harbin Institute of Technology, 2017: 38-55(in Chinese). [3] 严恭敏, 邓瑀. 传统组合导航中的实用Kalman滤波技术评述[J]. 导航定位与授时, 2020, 7(2): 50-64. https://www.cnki.com.cn/Article/CJFDTOTAL-DWSS202002009.htmYAN G M, DENG Y. Review on practical Kalman filtering techniques in traditional integrated navigation system[J]. Navigation Positioning and Timing, 2020, 7(2): 50-64(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DWSS202002009.htm [4] SONG J L, SHI Z Y, DU B H, et al. MEMS gyroscope wavelet de-noising method based on redundancy and sparse representation[J]. Microelectronic Engineering, 2019, 217(9): 111112.1-111112.11. http://www.sciencedirect.com/science/article/pii/S0167931719302680 [5] ZHU Z S, BO Y M, JIANG C H, et al. A MEMS gyroscope noise suppressing method using neural architecture search neural network[J]. Mathematical Problems in Engineering, 2019(1): 1-9. http://www.researchgate.net/publication/337048905_A_MEMS_Gyroscope_Noise_Suppressing_Method_Using_Neural_Architecture_Search_Neural_Network [6] 刘孝博, 陈光武, 王迪, 等. MEMS陀螺仪漂移和噪声的分析和补偿[J]. 传感技术学报, 2018, 31(3): 368-373. doi: 10.3969/j.issn.1004-1699.2018.03.009LIU X B, CHEN G W, WANG D, et al. Analysis and compensation of drift and noise in MEMS gyroscope[J]. Chinese Journal of Sensors and Actuators, 2018, 31(3): 368-373(in Chinese). doi: 10.3969/j.issn.1004-1699.2018.03.009 [7] 刘文涛, 刘洁瑜, 沈强. 光纤陀螺随机误差的集成建模及滤波处理[J]. 光电工程, 2018, 45(10): 53-61. https://www.cnki.com.cn/Article/CJFDTOTAL-GDGC201810008.htmLIU W T, LIU J Y, SHEN Q. Integrated modeling and filtering of fiber optic gyroscope's random errors[J]. Opto-Electronic Engineering, 2018, 45(10): 53-61(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDGC201810008.htm [8] 杨菊花, 刘洋, 陈光武, 等. 基于改进EMD的微机械陀螺随机误差建模方法[J]. 仪器仪表学报, 2019, 40(12): 196-204. https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201912021.htmYANG J H, LIU Y, CHEN G W, et al. A modeling method for random errors of micromechanical gyroscope based on the improved EMD[J]. Chinese Journal of Scientific Instrument, 2019, 40(12): 196-204(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201912021.htm [9] 纪涛, 孙长库, 何晶晶, 等. MEMS惯性陀螺仪随机误差自适应补偿方法[J]. 电光与控制, 2020, 27(11): 97-100. doi: 10.3969/j.issn.1671-637X.2020.11.019JI T, SUN C K, HE J J, et al. Adaptive compensation method for random errors of MEMS inertial gyroscope[J]. Electronics Optics and Control, 2020, 27(11): 97-100(in Chinese). doi: 10.3969/j.issn.1671-637X.2020.11.019 [10] 严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2015: 92-94.YAN G M, LI S H, QIN Y Y. Inertial instrument test and data analysis[M]. Beijing: National Defense Industry Press, 2015: 92-94(in Chinese). [11] 段志强, 刘洁瑜, 汪立新, 等. BPNN辅助KF的MEMS陀螺仪数据处理方法[J]. 压电与声光, 2020, 42(2): 284-288. https://www.cnki.com.cn/Article/CJFDTOTAL-YDSG202002032.htmDUAN Z Q, LIU J Y, WANG L X, et al. Research on data processing method of MEMS gyroscope based on BPNN assisted Kalman filter[J]. Piezoelectrics & Acoustooptics, 2020, 42(2): 284-288(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YDSG202002032.htm [12] 王可东, 武雨霞. 一种MEMS陀螺随机漂移的高精度建模方法[J]. 北京航空航天大学学报, 2016, 42(8): 1584-1592. doi: 10.13700/j.bh.1001-5965.2015.0510WANG K D, WU Y X. An accurate modeling method for random drift of MEMS gyro[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1584-1592(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0510 [13] BAI Y T, WANG X Y, JIN X B, et al. Adaptive filtering for MEMS gyroscope with dynamic noise model[J]. ISA transactions, 2020, 101: 430-441. doi: 10.1016/j.isatra.2020.01.030 [14] 耿梦梦, 任元, 樊亚洪, 等.MSCSG随机误差测试及误差源分析[J/OL].北京航空航天大学学报, 2020(2020-07-28)[2020-12-01].https://doi.org/10.13700/j.bh.1001-5965.2020.0269.GENG M M, REN Y, FAN Y H, et al.Random error measurement and error source analysis of MSCSG[J/OL].Journal of Beijing University of Aeronautics and Astronautics, 2020(2020-07-28)[2020-12-01].https://doi.org/10.13700/j.bh.1001-5965.2020.0269 (in Chinese). [15] 李想, 汪立新, 沈强. 基于改进GM(1, 1)模型的激光陀螺仪随机误差预测[J]. 光学学报, 2020, 40(12): 42-49. https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB202012005.htmLI X, WANG L X, SHENG Q. Prediction of the random error of a laser gyroscope using the modified GM(1, 1) model[J]. Acta Optica Sinica, 2020, 40(12): 42-49(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB202012005.htm [16] 王新龙, 李娜. MEMS陀螺随机误差的建模与分析[J]. 北京航空航天大学学报, 2012, 38(2): 170-174. https://bhxb.buaa.edu.cn/CN/Y2012/V/I2/170WANG X L, LI N. Error modeling and analysis for random drift of MEMS gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 170-174(in Chinese). https://bhxb.buaa.edu.cn/CN/Y2012/V/I2/170 -
下载:
点击查看大图
计量
- 文章访问数: 703
- HTML全文浏览量: 142
- PDF下载量: 226
- 被引次数: 0
