-
摘要:
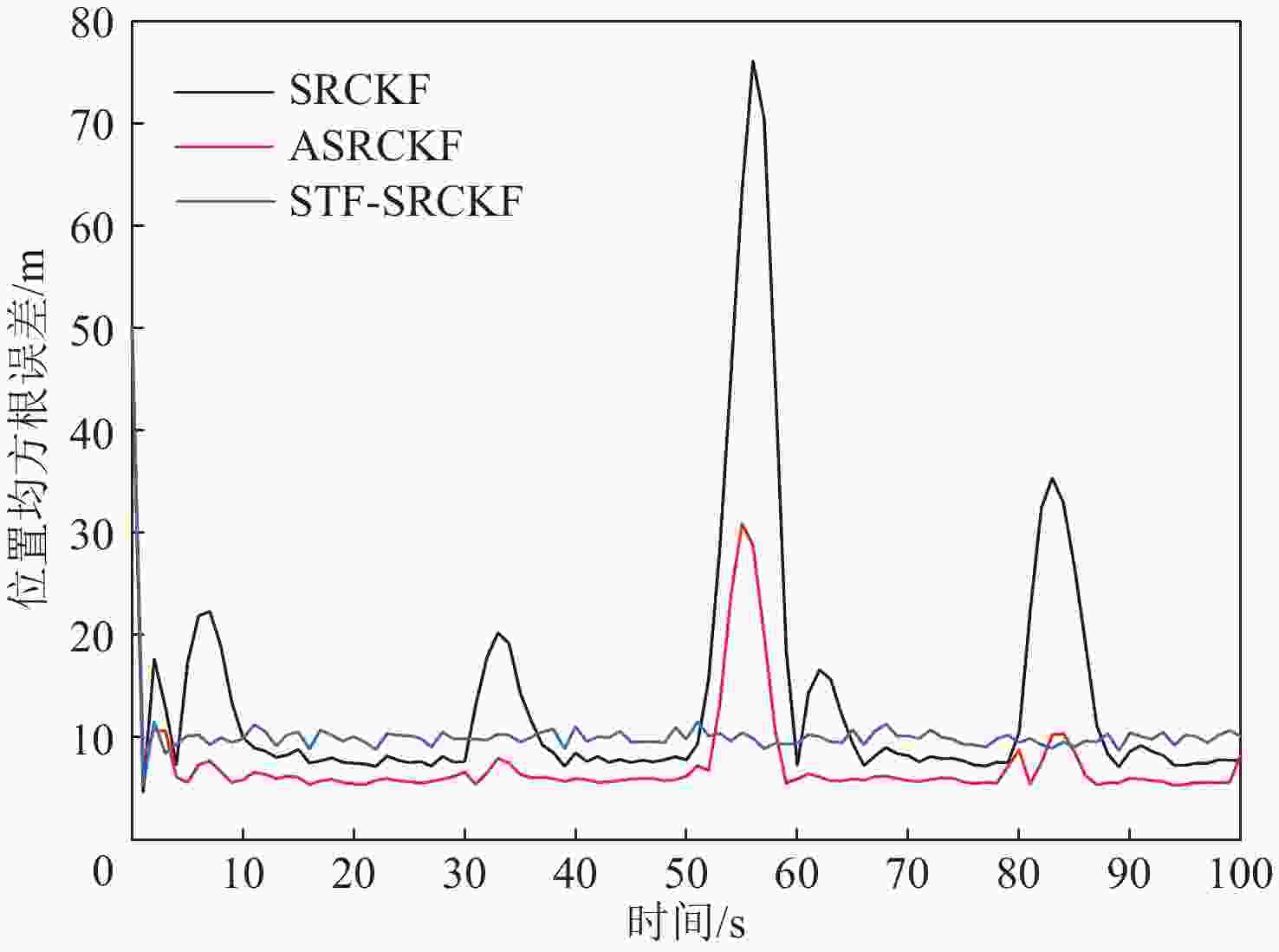
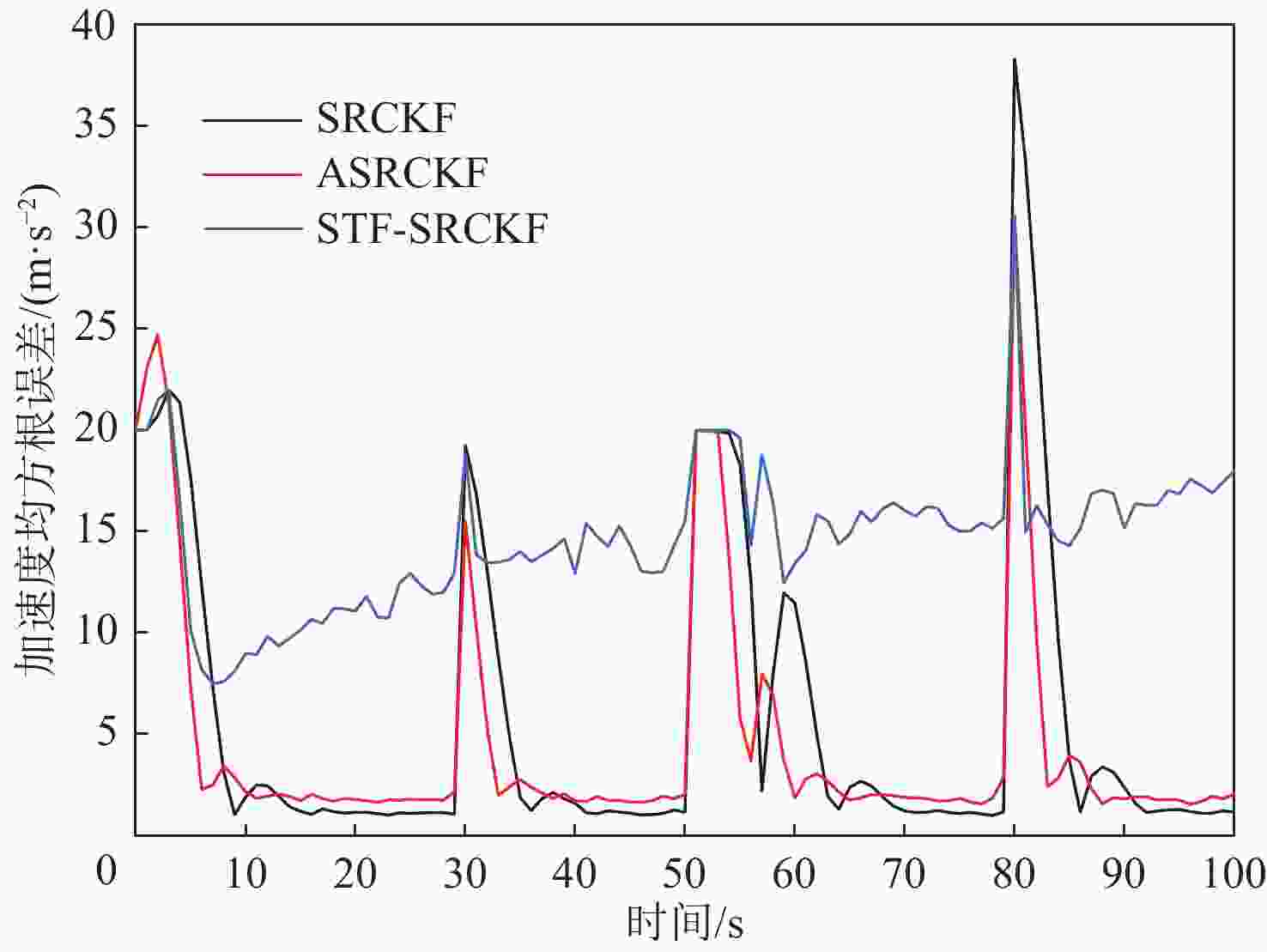
目标跟踪过程中的模型误差会使得平方根容积卡尔曼滤波(SRCKF)性能下降,滤波精度降低;自适应滤波中的修正卡尔曼滤波(AKF)算法可以有效解决这一问题,但是难以应用到非线性滤波中。为了克服模型误差带来的不利影响,同时,进一步提高修正思想的应用范围,在SRCKF的基础上,基于最小化新息协方差准则推导了修正系数的向量形式,提出修正SRCKF(ASRCKF)算法。所提算法通过利用后期的测量数据,增加对测量值的信任度,从而达到对目标模型误差进行补偿的目的。仿真结果表明:与SRCKF和强跟踪SRCKF算法相比,所提ASRCKF算法能有效抑制模型误差,有着更优的滤波性能。
-
关键词:
- 修正卡尔曼滤波 /
- 运动模型误差 /
- 平方根容积卡尔曼滤波 /
- 新息协方差 /
- 修正系数
Abstract:The model errors in the target tracking process will lead to the degraded performance and decreased filtering accuracy of the square-root cubature Kalman filter (SRCKF). Amended Kalman filter (AKF) can solve this problem effectively, but it is difficult to be applied to nonlinear filtering. To overcome the negative impact of the model errors and to further improve the application scope of the amendment thought, the vector form of the amendment coefficient is derived by minimizing innovation covariance on the basis of the SRCKF. Then, the amended SRCKF (ASRCKF) algorithm is proposed. By using posterior measurements, the ASRCKF algorithm can increase confidence level to measurement, so that the target model error can be compensated. The simulation results indicate the ASRCKF can suppress the model errors effectively with better filtering performance, compared with SRCKF and STF-SRCKF algorithms.
-
表 1 场景1误差均值对比
Table 1. Comparison of mean error for each algorithm in case 1
算法 位置误差
均值/m速度误差
均值/(m·s−1)加速度误差
均值/(m·s−2)SRCKF 7.970 7 6.984 2 2.808 3 ASRCKF 4.752 0 4.119 1 2.320 1 STF-SRCKF 7.520 7 14.643 5 10.654 1 表 2 场景2误差均值对比
Table 2. Comparison of mean error for each algorithm in case 2
算法 位置误差
均值/m速度误差
均值/(m·s−1)加速度误差
均值/(m·s−2)SRCKF 12.5175 13.1114 5.6948 ASRCKF 6.4368 6.7186 4.2920 STF-SRCKF 8.2924 16.1961 12.1711 -
[1] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. doi: 10.1109/TAC.2009.2019800 [2] ARASARATNAM I, HAYKIN S, HURD T R. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4977-4993. doi: 10.1109/TSP.2010.2056923 [3] 王小旭, 潘泉, 黄鹤, 等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策, 2012, 27(6): 801-812. doi: 10.13195/j.cd.2012.06.4.wangxx.012WANG X X, PAN Q, HUANG H, et al. Overview of deterministic sampling filtering algorithms for nonlinear system[J]. Control and Decision, 2012, 27(6): 801-812(in Chinese). doi: 10.13195/j.cd.2012.06.4.wangxx.012 [4] CORTINA E, OTERO D, D’ATTELLIS C E. Maneuvering target tracking using extended Kalman filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(1): 155-158. doi: 10.1109/7.68158 [5] JULIER S, UHLMANN J, DURRANT-WHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482. doi: 10.1109/9.847726 [6] JULIER S J, UHLMANN J K. A general method for approximating nonlinear transformation of probability distributions [EB/OL]. (1996-11-01)[2021-04-05]. http://www.eng.ox.ac.uk/. [7] ZHAO L Q, WANG J L, YU T, et al. Design of adaptive robust square-root cubature Kalman filter with noise statistic estimator[J]. Applied Mathematics and Computation, 2015, 256: 352-367. doi: 10.1016/j.amc.2014.12.036 [8] 赵利强, 罗达灿, 王建林, 等. 自适应强跟踪容积卡尔曼滤波算法[J]. 北京化工大学学报(自然科学版), 2013, 40(3): 98-103.ZHAO L Q, LUO D C, WANG J L, et al. An adaptive strong tracking cubature Kalman filter[J]. Journal of Beijing University of Chemical Technology (Natural Science Edition), 2013, 40(3): 98-103(in Chinese). [9] ZHANG H W, XIE J W, GE J A, et al. Adaptive strong tracking square-root cubature Kalman filter for maneuvering aircraft tracking[J]. IEEE Access, 2018, 6: 10052-10061. doi: 10.1109/ACCESS.2018.2808170 [10] ZHANG H W, XIE J W, GE J A, et al. Strong tracking SCKF based on adaptive CS model for manoeuvring aircraft tracking[J]. IET Radar, Sonar & Navigation, 2018, 12(7): 742-749. [11] HAN B, HUANG H Q, LEI L, et al. An improved IMM algorithm based on STSRCKF for maneuvering target tracking[J]. IEEE Access, 2019, 7: 57795-57804. doi: 10.1109/ACCESS.2019.2912983 [12] 徐天河, 杨元喜. 改进的Sage自适应滤波方法[J]. 测绘科学, 2000, 25(3): 22-24. doi: 10.3771/j.issn.1009-2307.2000.03.005XU T H, YANG Y X. The improved method of sage adaptive filtering[J]. Developments in Surveying and Mapping, 2000, 25(3): 22-24(in Chinese). doi: 10.3771/j.issn.1009-2307.2000.03.005 [13] 鲁平, 赵龙, 陈哲. 改进的Sage-Husa自适应滤波及其应用[J]. 系统仿真学报, 2007, 19(15): 3503-3505. doi: 10.3969/j.issn.1004-731X.2007.15.034LU P, ZHAO L, CHEN Z. Improved sage-husa adaptive filtering and its application[J]. Journal of System Simulation, 2007, 19(15): 3503-3505(in Chinese). doi: 10.3969/j.issn.1004-731X.2007.15.034 [14] 周东华, 席裕庚, 张钟俊. 一种带多重次优渐消因子的扩展卡尔曼滤波器[J]. 自动化学报, 1991, 17(6): 689-695. doi: 10.16383/j.aas.1991.06.007ZHOU D H, XI Y G, ZHANG Z J. A suboptimal multiple fading extended Kalman filter[J]. Acta Automatica Sinica, 1991, 17(6): 689-695(in Chinese). doi: 10.16383/j.aas.1991.06.007 [15] 徐树生, 林孝工, 李新飞. 强跟踪自适应平方根容积卡尔曼滤波算法[J]. 电子学报, 2014, 42(12): 2394-2400. doi: 10.3969/j.issn.0372-2112.2014.12.009XU S S, LIN X G, LI X F. Strong tracking adaptive square-root cubature Kalman filter algorithm[J]. Acta Electronica Sinica, 2014, 42(12): 2394-2400(in Chinese). doi: 10.3969/j.issn.0372-2112.2014.12.009 [16] 徐树生, 林孝工, 赵大威, 等. 强跟踪SRCKF及其在船舶定位中的应用[J]. 仪器仪表学报, 2013, 34(6): 1266-1272. doi: 10.3969/j.issn.0254-3087.2013.06.010XU S S, LIN X G, ZHAO D W, et al. Strong tracking SRCKF and its application in vessel dynamic positioning[J]. Chinese Journal of Scientific Instrument, 2013, 34(6): 1266-1272(in Chinese). doi: 10.3969/j.issn.0254-3087.2013.06.010 [17] GE Q B, LI W B, WEN C L. SCKF-STF-CN: A universal nonlinear filter for maneuver target tracking[J]. Journal of Zhejiang University SCIENCE C, 2011, 12(8): 678-686. doi: 10.1631/jzus.C10a0353 [18] LI N, ZHU R H, ZHANG Y G. A strong tracking square root CKF algorithm based on multiple fading factors for target tracking[C]//2014 Seventh International Joint Conference on Computational Sciences and Optimization. Piscataway: IEEE Press, 2014 : 16-20. [19] ZHANG A, BAO S D, BI W H, et al. Low-cost adaptive square-root cubature Kalman filter for systems with process model uncertainty[J]. Journal of Systems Engineering and Electronics, 2016, 27(5): 945-953. doi: 10.21629/JSEE.2016.05.01 [20] ZHANG A, BAO S D, GAO F, et al. A novel strong tracking cubature Kalman filter and its application in maneuvering target tracking[J]. Chinese Journal of Aeronautics, 2019, 32(11): 2489-2502. doi: 10.1016/j.cja.2019.07.025 [21] 张浩为, 谢军伟, 葛佳昂, 等. 自适应CS模型的强跟踪平方根容积卡尔曼滤波算法[J]. 系统工程与电子技术, 2019, 41(6): 1186-1194. doi: 10.3969/j.issn.1001506X.2019.06.03ZHANG H W, XIE J W, GE J A, et al. Strong tracking square-root cubature Kalman filter over adaptive current statistical model[J]. Systems Engineering and Electronics, 2019, 41(6): 1186-1194(in Chinese). doi: 10.3969/j.issn.1001506X.2019.06.03 [22] 杨永建, 樊晓光, 王晟达, 等. 基于修正卡尔曼滤波的目标跟踪[J]. 系统工程与电子技术, 2014, 36(5): 846-851. doi: 10.3969/j.issn.1001-506X.2014.05.06YANG Y J, FAN X G, WANG S D, et al. Target tracking based on amendatory Kalman filter[J]. Systems Engineering and Electronics, 2014, 36(5): 846-851(in Chinese). doi: 10.3969/j.issn.1001-506X.2014.05.06 [23] YANG Y J, FAN X G, ZHUO Z F, et al. AFAKF for manoeuvring target tracking based on current statistical model[J]. IET Science, Measurement & Technology, 2016, 10(6): 637-643. [24] YANG Y J, FAN X G, ZHUO Z F, et al. Amended Kalman filter for maneuvering target tracking[J]. Chinese Journal of Electronics, 2016, 25(6): 1166-1171. doi: 10.1049/cje.2016.08.036 [25] YANG Y J, FAN X G, TANG S J, et al. Amended Kalman filtering with intermittent measurements in target tracking[J]. Journal of Information Science and Engineering, 2019, 35(6): 1329-1341. -






 下载:
下载: