Acoustic metasurfaces for stabilization of broadband unstable modes in high speed boundary layer
-
摘要:
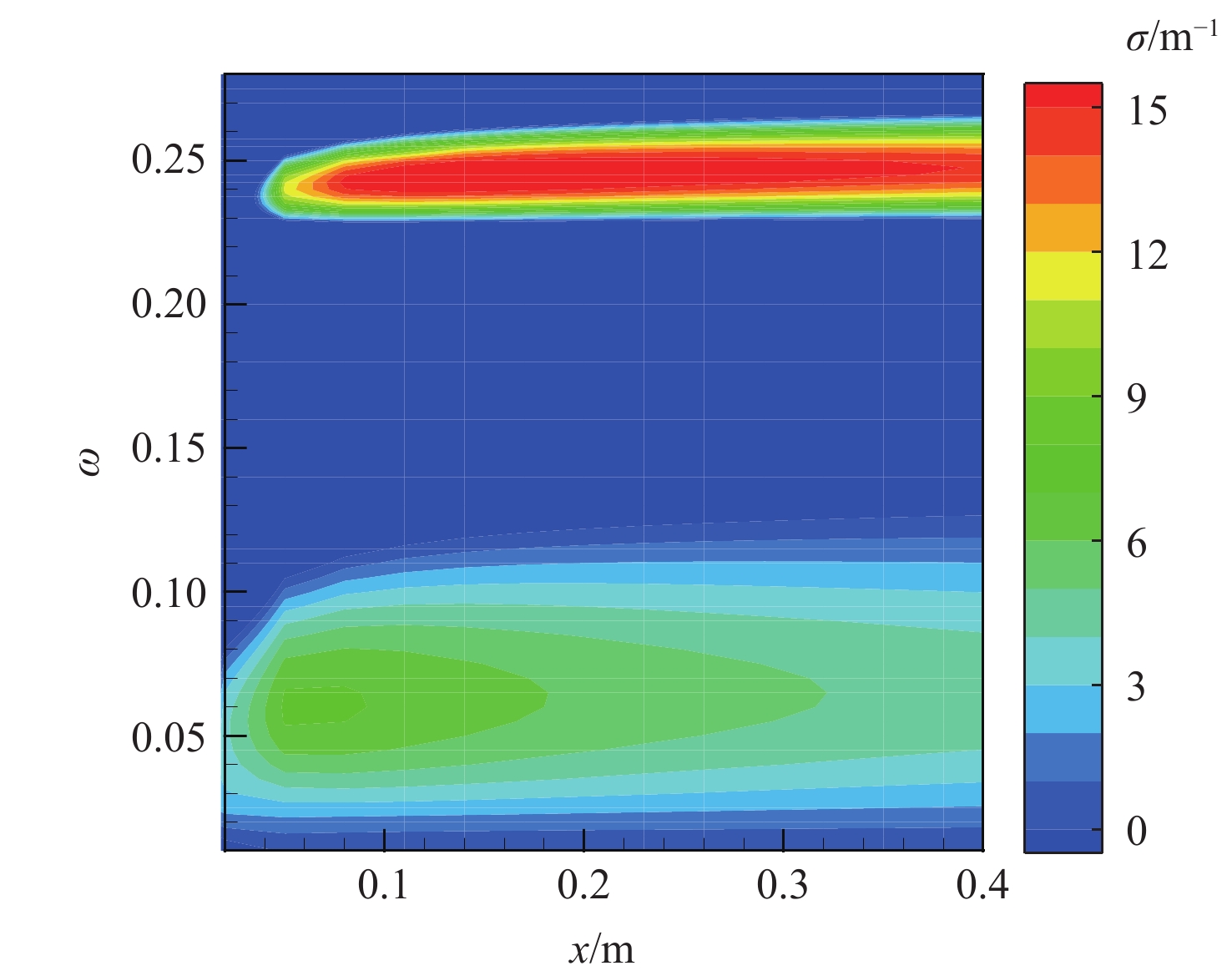
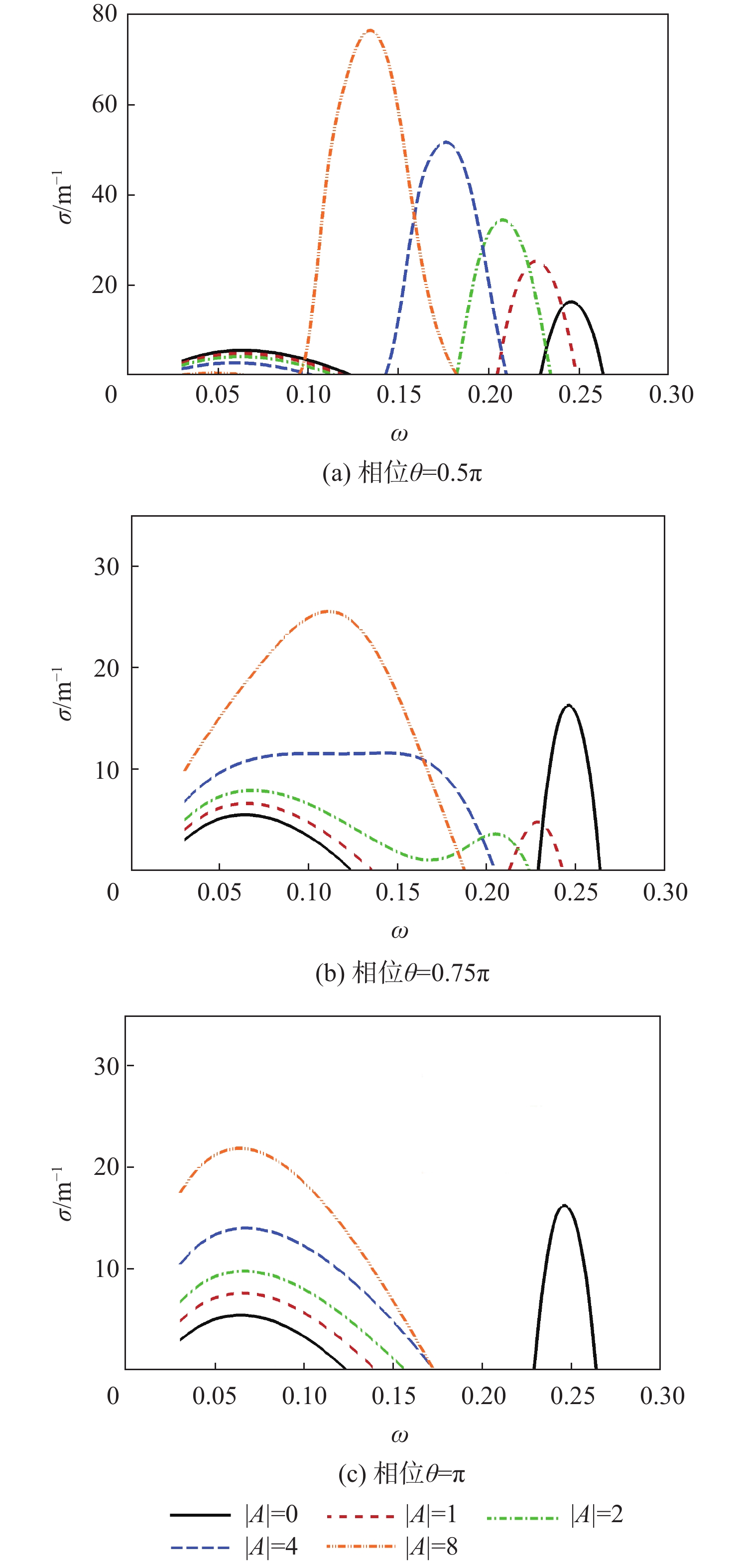
以声学超表面为研究对象，使用线性稳定性理论（LST），研究了声学超表面导纳相位与幅值对超声速平板边界层内宽频不稳定模态的影响规律。结果表明：当导纳相位
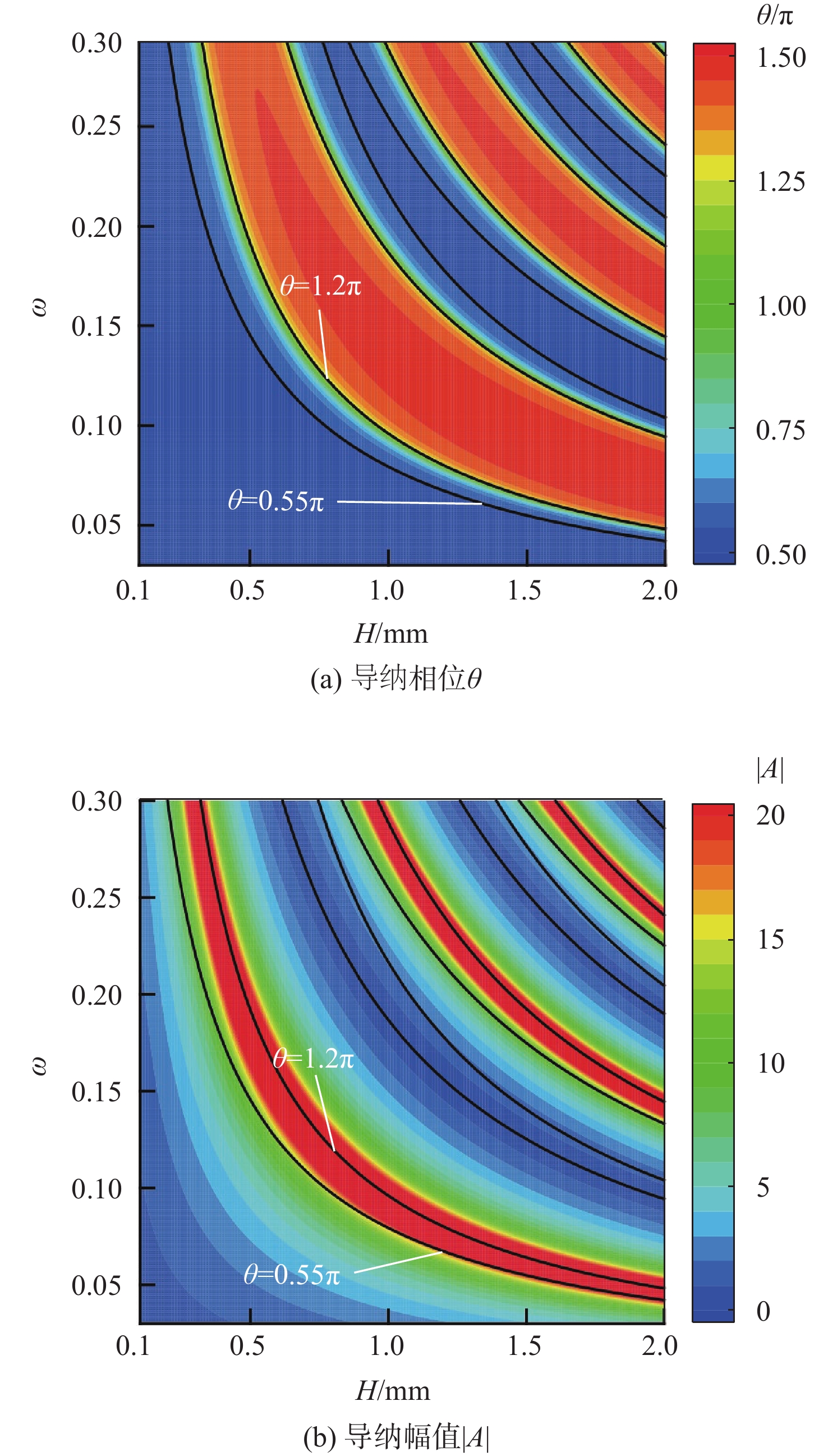
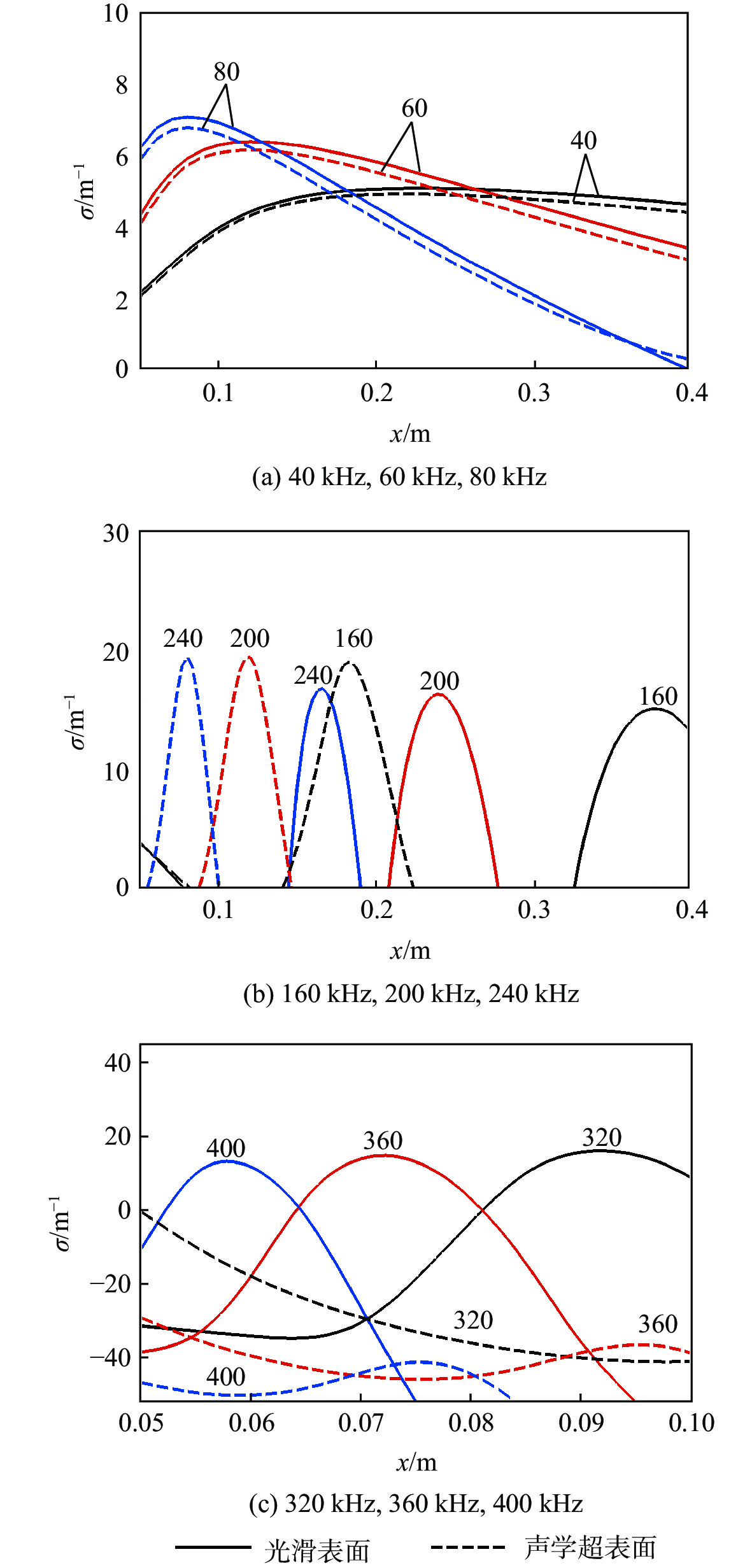
$ \theta $ 接近0.5$ \text{π}$ 时，第1模态被抑制的同时第2模态会被激发，且在较低频率范围内导纳幅值的增大能够使第1模态更加稳定；当导纳相位$ \theta $ 接近$ \text{π} $ 时，可抑制第2模态但同时激发第1模态；整体上，导纳幅值越大，对不稳定模态的抑制或激发效果越明显。在此基础上，结合缝隙几何参数对导纳的影响，提出一种可实现性宽频抑制方案，通过分段设计声学超表面微结构的几何尺寸，实现了同时抑制第1模态和高频第2模态的目标,并使用$ {\mathrm{e}}^{N} $ 方法验证了转捩抑制效果。Abstract:The influences of the admittance phase and amplitude of acoustic metasurfaces on the broadband unstable modes in a high-speed flat plate boundary layer are analyzed using linear stability theory (LST). It is demonstrated that when the admittance phase goes to 0.5 π, the first mode is suppressed while the second mode is simultaneously motivated. Moreover, the increase of amplitude within the lower frequency range can enhance the stability of the first mode. The Mack second mode is suppressed when the admittance phase tends to π, while the first mode is motivated. Generally, the larger the admittance amplitude is, the more obvious the suppression or excitation effect of unstable modes becomes. Besides, combined with the effect of aperture geometry parameters on the admittance, an engineering realizable broadband acoustic metasurface is proposed to suppress both the first and Mack second modes in Mach 4 boundary layer flow. It elaborately designs the piecewise microstructures to achieve the local favorite admittance phase and amplitude, and its performance is verified by the
$ {\mathrm{e}}^{N} $ method. -
图 1 缝隙型声学超表面的示意图
Figure 1. Schematic diagram of the aperture type acoustic metasurface
图 3 声学超表面导纳相位与幅值对不稳定模态增长率的影响
Figure 3. Effects of admittance phase and amplitude of acoustic metasurface on the growth rates of unstable modes
图 4 不同导纳相位对第1模态增长率的影响
Figure 4. Effects of admittance phase on the growth rates of the first mode
图 9 不同频率下扰动模态在声学超表面与光滑表面的增长率对比
Figure 9. Growth rates of unstable modes at different frequencies on acoustic metasurface and smooth surface
图 10 声学超表面与光滑表面的N值曲线对比
Figure 10. Comparisons of N-value curves of acoustic metasurface and smooth surface
图 11 声学超表面与光滑表面N值包络线对比
Figure 11. Comparisons of N-value envelopments of acoustic metasurface and smooth surface
表 1 不同
${\boldsymbol{x}} $ 位置处的最优缝隙参数Table 1. Optimal gap parameters at different
${\boldsymbol{x}} $ positions流向位置x/m H/mm n Ar 0.10 0.28 0.12 0.7 0.15 0.37 0.12 0.7 0.20 0.44 0.13 0.7 0.25 0.51 0.13 0.7 0.30 0.57 0.14 0.7 0.35 0.63 0.14 0.7 0.40 0.68 0.14 0.7 
下载: 导出CSV
-
[1] 陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337.CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition: What we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337(in Chinese). [2] FEDOROV A V, MALMUTH N D, RASHEED A, et al. Stabilization of hypersonic boundary layers by porous coatings[J]. AIAA Journal, 2001, 39(4): 605-610. doi: 10.2514/2.1382 [3] RILEY Z B, DESHMUKH R, MILLER B A, et al. Characterization of structural response to hypersonic boundary-layer transition[J]. AIAA Journal, 2016, 54(8): 2418-2431. doi: 10.2514/1.J054607 [4] 李锋, 解少飞, 毕志献, 等. 高超声速飞行器中若干气动难题的实验研究[J]. 现代防御技术, 2014, 42(5): 1-7. doi: 10.3969/j.issn.1009-086x.2014.05.001LI F, XIE S F, BI Z X, et al. Experimental study of several on aerodynamic problems on hypersonic vehicles[J]. Modern Defence Technology, 2014, 42(5): 1-7(in Chinese). doi: 10.3969/j.issn.1009-086x.2014.05.001 [5] MORKOVIN M, RESHOTKO E, HERBERT T. Transition in open flow systems-a reassessment[J]. Bulletin of the American Physical Society, 1994, 39(9): 1882. [6] RESHOTKO E. Boundary layer instability, transition and control[C]// 32nd Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1994: 1. [7] WAGNER A, KUHN M, MARTINEZ SCHRAMM J, et al. Experiments on passive hypersonic boundary layer control using ultrasonically absorptive carbon–carbon material with random microstructure[J]. Experiments in Fluids, 2013, 54(10): 1-10. [8] ZHAO R, LIU T, WEN C Y, et al. Impedance-near-zero acoustic metasurface for hypersonic boundary-layer flow stabilization[J]. Physical Review Applied, 2019, 11(4): 044015. doi: 10.1103/PhysRevApplied.11.044015 [9] MA Y B, ZHONG X L. Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions[J]. Journal of Fluid Mechanics, 2003, 488: 31-78. doi: 10.1017/S0022112003004786 [10] FEDOROV A, TUMIN A. High-speed boundary-layer instability: Old terminology and a new framework[J]. AIAA Journal, 2011, 49(8): 1647-1657. doi: 10.2514/1.J050835 [11] BITTER N P, SHEPHERD J E. Stability of highly cooled hypervelocity boundary layers[J]. Journal of Fluid Mechanics, 2015, 778: 586-620. doi: 10.1017/jfm.2015.358 [12] MACK L M. Boundary-layer linear stability theory, N84-33757[R]. [S.l]: The NASA Astrophysis Data System, 1984: 23-34. [13] RASHEED A, HORNUNG H G, FEDOROV A V, et al. Experiments on passive hypervelocity boundary-layer control using an ultrasonically absorptive surface[J]. AIAA Journal, 2002, 40(3): 481-489. doi: 10.2514/2.1671 [14] 涂国华, 陈坚强, 袁先旭, 等. 多孔表面抑制第二模态失稳的最优开孔率和孔半径分析[J]. 空气动力学学报, 2018, 36(2): 273-278.TU G H, CHEN J Q, YUAN X X, et al. Optimal porosity and pore radius of porous surfaces for damping the second-mode instability[J]. Acta Aerodynamica Sinica, 2018, 36(2): 273-278(in Chinese). [15] ZHAO R, LIU T, WEN C Y, et al. Theoretical modeling and optimization of porous coating for hypersonic laminar flow control[J]. AIAA Journal, 2018, 56(8): 2942-2946. doi: 10.2514/1.J057272 [16] ZHAO R, ZHANG X X, WEN C Y. Theoretical modeling of porous coatings with simple microstructures for hypersonic boundary-layer stabilization[J]. AIAA Journal, 2019, 58(2): 981-986. [17] ZHAO R, WEN C Y, LONG T H, et al. Spatial direct numerical simulation of the hypersonic boundary-layer stabilization using porous coatings[J]. AIAA Journal, 2019, 57(11): 5061-5065. doi: 10.2514/1.J058467 [18] 郭启龙, 涂国华, 陈坚强, 等. 横向矩形微槽对高超边界层失稳的控制作用[J]. 航空动力学报, 2020, 35(1): 135-143. doi: 10.13224/j.cnki.jasp.2020.01.016GUO Q L, TU G H, CHEN J Q, et al. Control of hypersonic boundary layer instability by transverse rectangular micro-cavities[J]. Journal of Aerospace Power, 2020, 35(1): 135-143(in Chinese). doi: 10.13224/j.cnki.jasp.2020.01.016 [19] TU G H, CHEN J F, WAN B B, et al. Investigation on correlation between wind tunnel and flight for boundary layer stability and transition of MF-1 blunt cone[J]. Scientia Sinica, 2019, 49(12): 124701. [20] 刘强, 涂国华, 罗振兵, 等. 延迟高超声速边界层转捩技术研究进展[J]. 航空学报, 2022, 43(7): 25357. doi: 10.7527/j.issn.1000-6893.2022.7.hkxb202207001LIU Q, TU G H, LUO Z B, et al. Progress in hypersonic boundary layer transition delay control[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(7): 25357(in Chinese). doi: 10.7527/j.issn.1000-6893.2022.7.hkxb202207001 [21] FEDOROV A, SHIPLYUK A, MASLOV A, et al. Stabilization of a hypersonic boundary layer using an ultrasonically absorptive coating[J]. Journal of Fluid Mechanics, 2003, 479: 99-124. doi: 10.1017/S0022112002003440 [22] WANG X W, ZHONG X L. The stabilization of a hypersonic boundary layer using local sections of porous coating[J]. Physics of Fluids, 2012, 24(3): 034105. doi: 10.1063/1.3694808 [23] WANG X W, ZHONG X L. Phase angle of porous coating admittance and its effect on boundary-layer stabilization[C]// 41st AIAA Fluid Dynamics Conference and Exhibit. Reston: AIAA, 2011: 3080. [24] TIAN X, ZHAO R, LONG T, et al. Reverse design of ultrasonic absorptive coating for the stabilization of mack modes[J]. AIAA Journal, 2019, 57(6): 2264-2269. doi: 10.2514/1.J058105 [25] 赵瑞, 严昊, 席柯, 等. 声学超表面抑制第一模态研究[J]. 航空科学技术, 2020, 31(11): 104-112. doi: 10.19452/j.issn1007-5453.2020.11.013ZHAO R, YAN H, XI K, et al. Research on acoustic metasurfaces for the suppression of the first mode[J]. Aeronautical Science & Technology, 2020, 31(11): 104-112(in Chinese). doi: 10.19452/j.issn1007-5453.2020.11.013 [26] MACK L M. Linear stability theory and the problem of supersonic boundary- layer transition[J]. AIAA Journal, 1975, 13(3): 278-289. doi: 10.2514/3.49693 [27] MALIK M R. Numerical methods for hypersonic boundary layer stability[J]. Journal of Computational Physics, 1990, 86(2): 376-413. doi: 10.1016/0021-9991(90)90106-B [28] EL-HADY N M. Nonparallel stability of three-dimensional compressible boundary layers. Part 1: Stability analysis: NASA-CR-3245 [R]. Washington, D. C. : National Aeronautics and Space Administration, 1980: 1-38. [29] MALIK M, MALIK M. Boundary-layer transition prediction toolkit[C]//28th Fluid Dynamics Conference. Reston: AIAA, 1997: 1904. [30] 罗纪生. 高超声速边界层的转捩及预测[J]. 航空学报, 2015, 36(1): 357-372.LUO J S. Transition and prediction for hypersonic boundary layers[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357-372(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 313
- HTML全文浏览量: 113
- PDF下载量: 31
- 被引次数: 0
