基于组合优化算法的空面导弹全空域弹道优化

祝雯生; 吕先敬; 侯振乾; 张顺家; 毕鹏; 仲康

doi:10.13700/j.bh.1001-5965.2021.0252

基于组合优化算法的空面导弹全空域弹道优化

doi: 10.13700/j.bh.1001-5965.2021.0252

1.
上海机电工程研究所，上海 201109
2.
空军装备部驻上海地区军事代表局，上海 200030

详细信息

通讯作者:
E-mail： whzhu@nuaa.edu.cn

中图分类号: V448.13
计量
- 文章访问数: 418
- HTML全文浏览量: 75
- PDF下载量: 36
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-14
- 录用日期: 2021-06-29
- 网络出版日期: 2021-07-06
- 整期出版日期: 2023-02-28

Trajectory optimization of air-to-surface missile in full airspace based on combinational optimization algorithm

1.
Shanghai Electro-Mechanical Engineering Institute，Shanghai 201109，China
2.
The Military Representative Bureau of Equipment Department in Shanghai，Shanghai 200030，China

More Information

Corresponding author: E-mail： whzhu@nuaa.edu.cn

摘要

摘要:
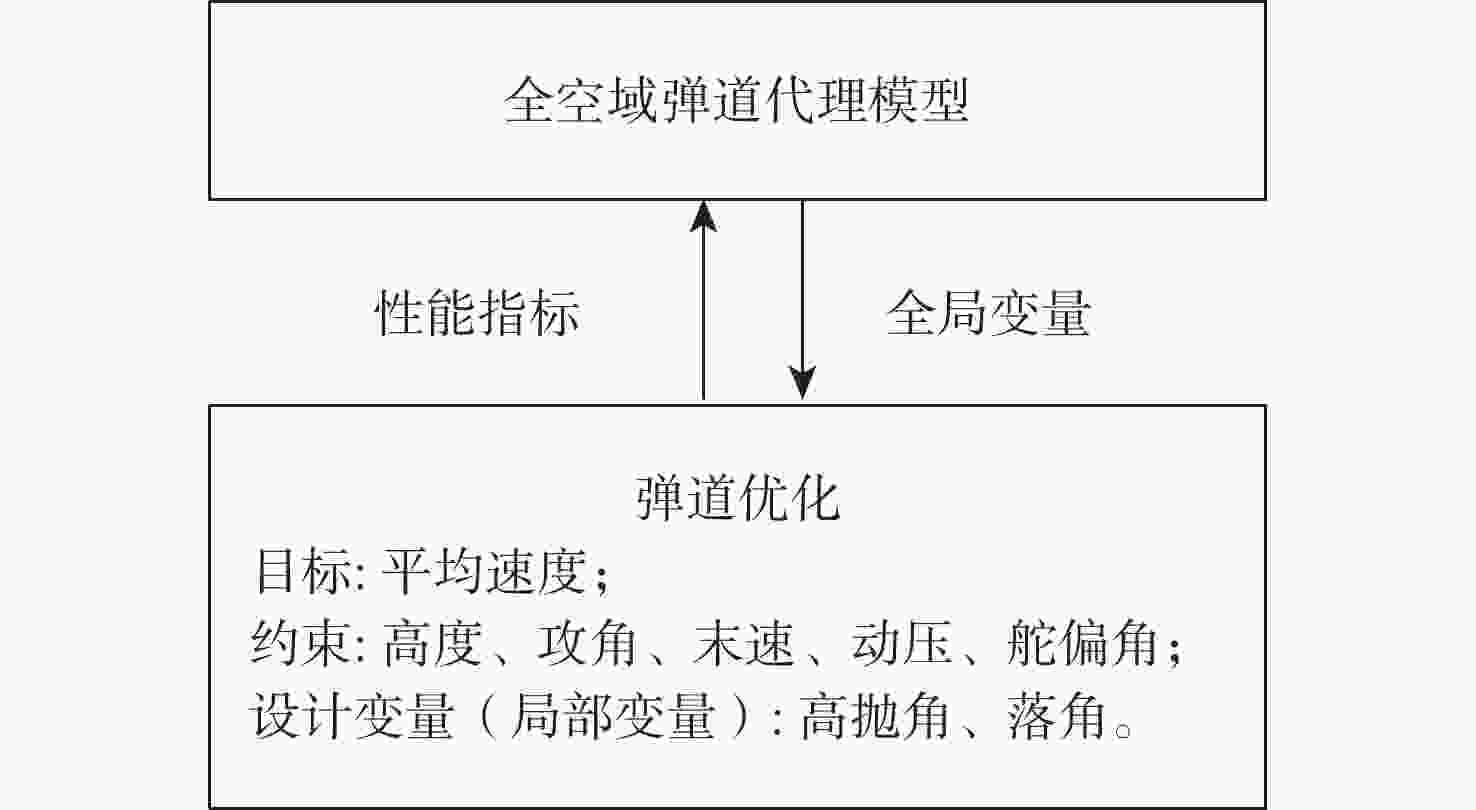
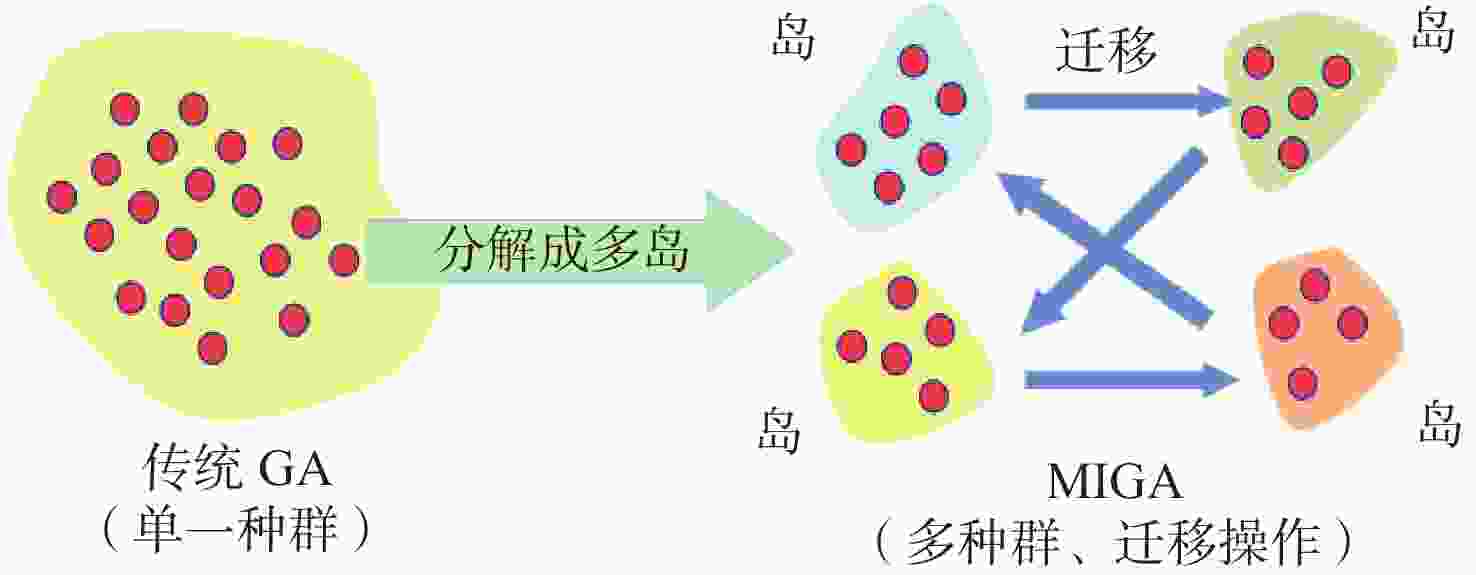
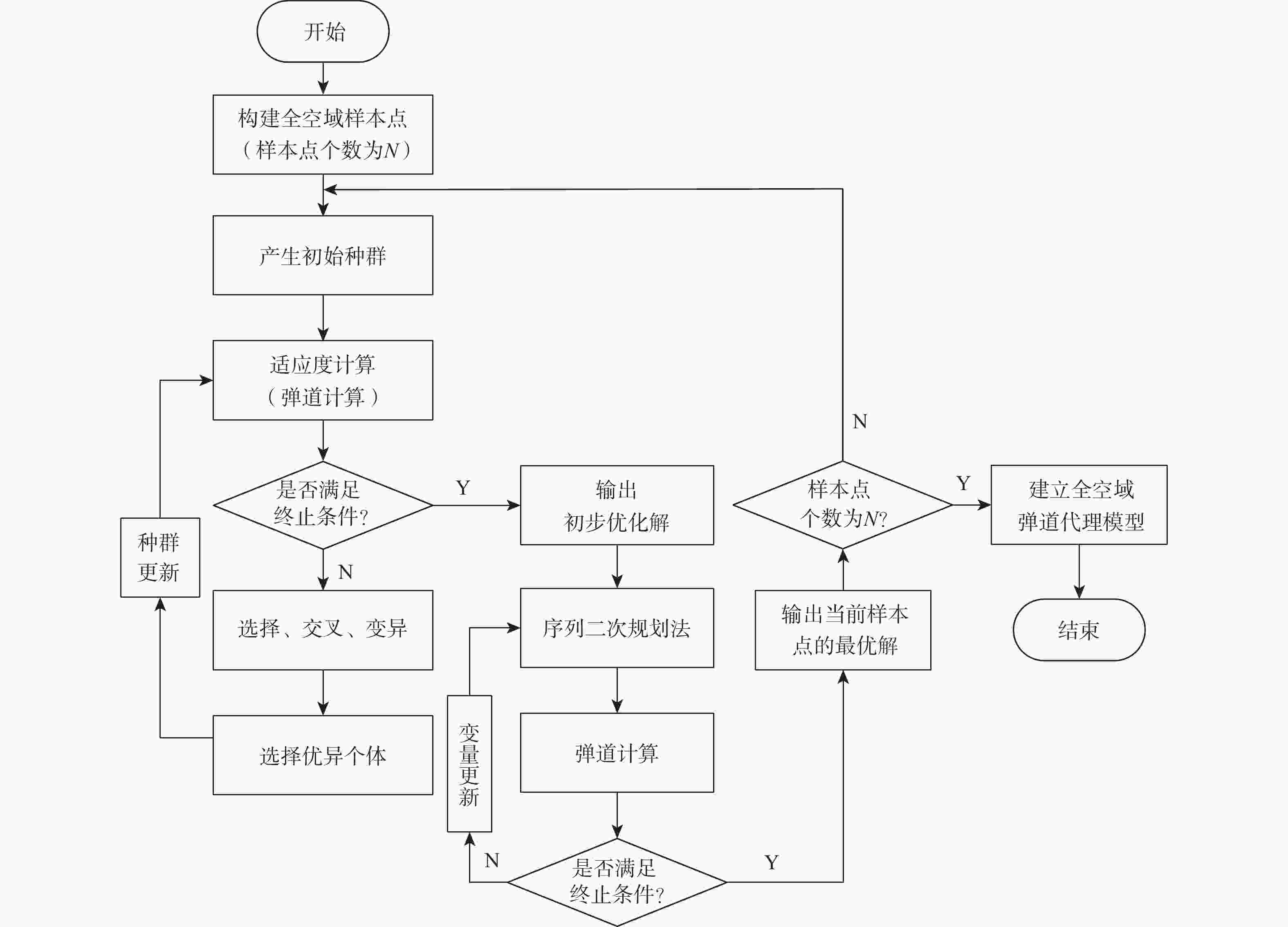
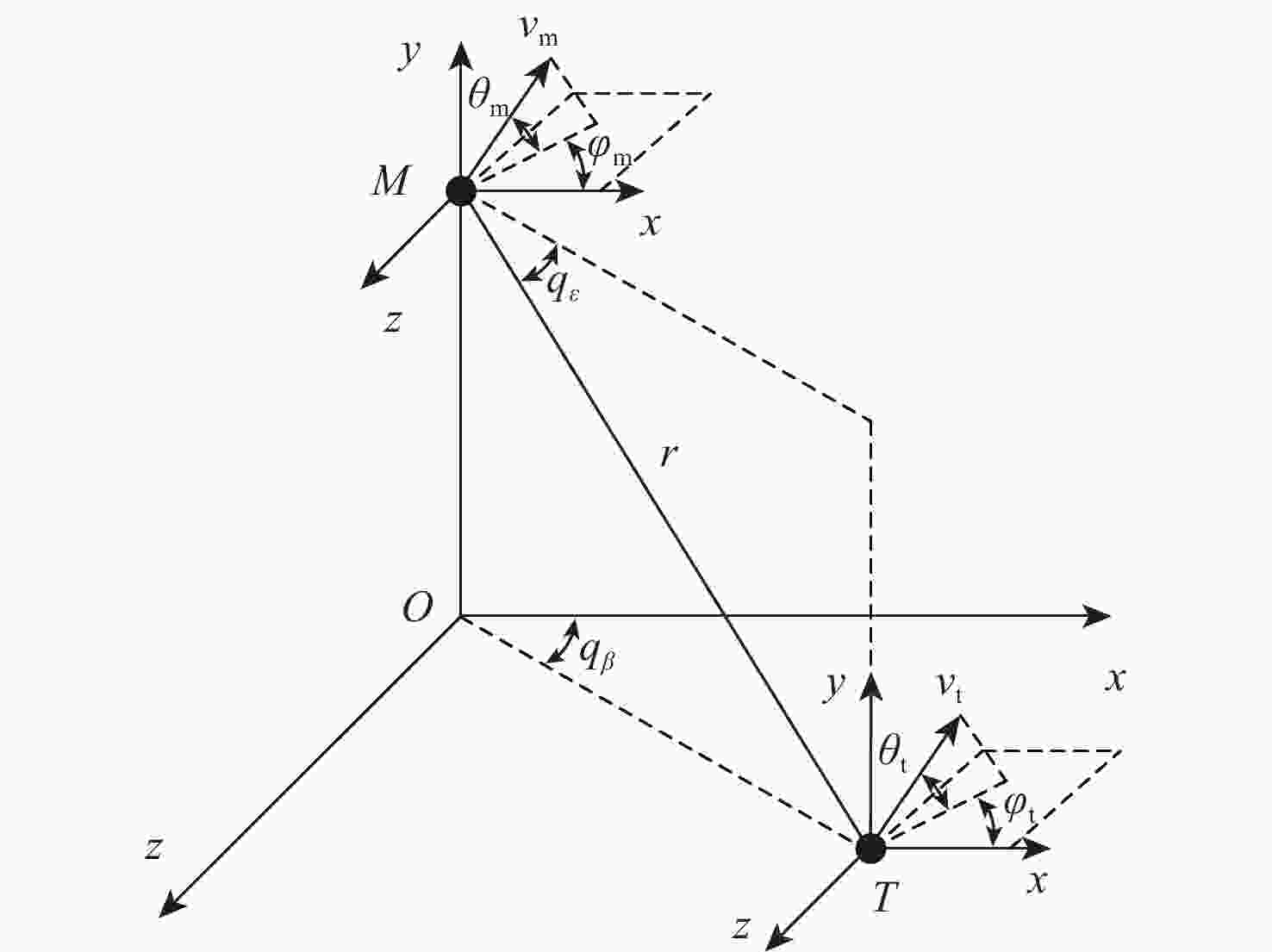
针对空面导弹全空域弹道优化问题，提出基于多岛遗传算法和序列二次规划法的组合优化算法，充分发挥多岛遗传算法对初值不敏感、全局收敛性强及序列二次规划法收敛速度快、精度高等特点。采用代理模型技术，在保证拟合精度的前提下，极大的降低了全空域弹道优化的计算量。算例结果表明：组合优化算法收敛速度较快，可以得到高精度的全局最优解；代理模型拟合精度较高，可以满足工程要求；且优化结果和所建立的代理模型可以为全空域制导律设计提供有力的支撑。
- 空面导弹 /
- 全空域 /
- 弹道优化 /
- 多岛遗传算法 /
- 序列二次规划法
Abstract:
To deal with the problem of trajectory optimization for the air-to-surface missile in full airspace, a combinational optimization algorithm based on a multi-island genetic algorithm (MIGA) and sequential quadratic programming (SQP) was proposed. The advantages of being insensitive to initial values and global convergence of MIGA, and rapid convergence and high precision of SQP were developed. With the surrogate model, the computational cost of trajectory optimization in full airspace was greatly reduced on the premise of ensuring fitting precision. The surrogate model significantly lowered the computing cost of trajectory optimization in full airspace under the assumption of fitting precision. Results show that the combinational optimization algorithm had a rapid convergence speed and could obtain a global high-precision solution; the surrogate model had high fitting precision and could satisfy the requirements of engineering; the optimization results and surrogate model could provide an effective way for the design of guidance law in full airspace.
- air-to-surface missile /
- full airspace /
- trajectory optimization /
- multi-island genetic algorithm /
- sequential quadratic programming

HTML全文

图 1 弹目相对运动示意图

Figure 1. Schematic diagram of relative motion between missile and target

下载: 全尺寸图片幻灯片

图 2 空面导弹典型飞行过程

Figure 2. Typical flight process of air-to-surface missile

下载: 全尺寸图片幻灯片

图 3 全空域弹道2级优化框架

Figure 3. Two-level optimization framework for trajectory optimization in full airspace

下载: 全尺寸图片幻灯片

图 4 传统GA和MIGA对比

Figure 4. Comparison between traditional GA and MIGA

下载: 全尺寸图片幻灯片

图 5 全空域弹道优化流程

Figure 5. Flowchart of trajectory optimization in full airspace

下载: 全尺寸图片幻灯片

图 6 平均速度迭代收敛结果

Figure 6. Iteration convergence results history of average velocity

下载: 全尺寸图片幻灯片

图 7 2种发射条件下优化前后弹道曲线

Figure 7. Trajectory before and after optimization under two launch conditions

下载: 全尺寸图片幻灯片

图 8 2种发射条件下优化前后速度曲线

Figure 8. Velocity curve before and after optimization under two launch conditions

下载: 全尺寸图片幻灯片

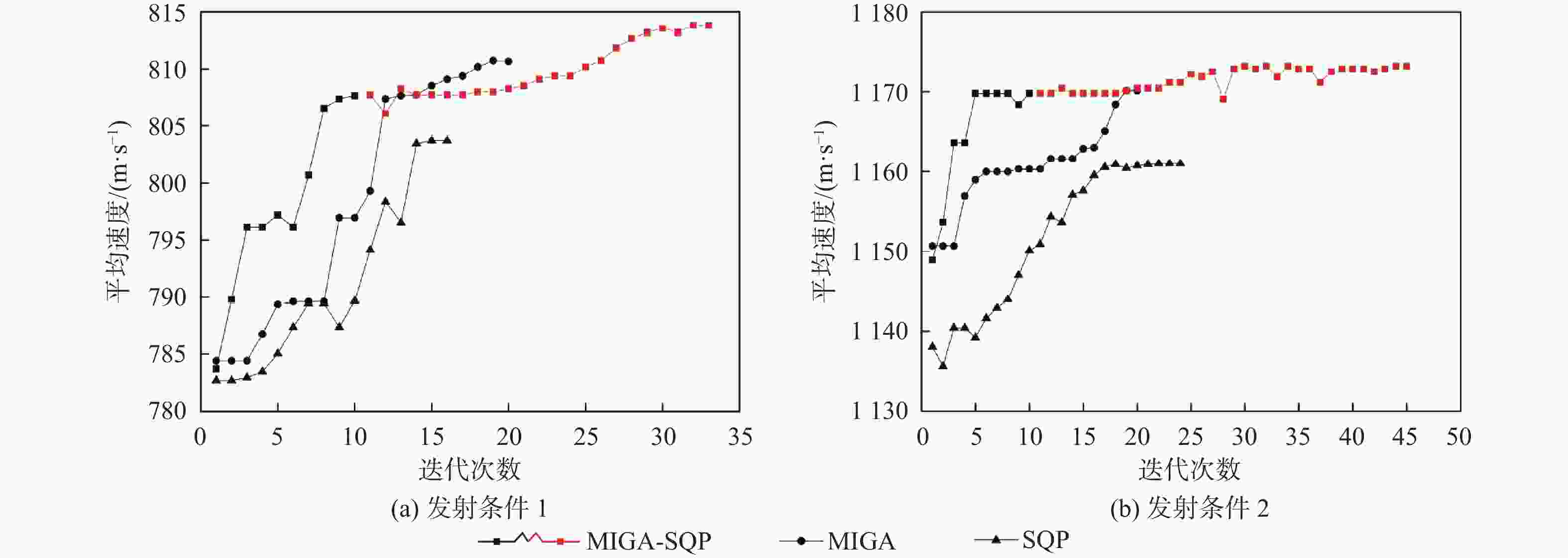
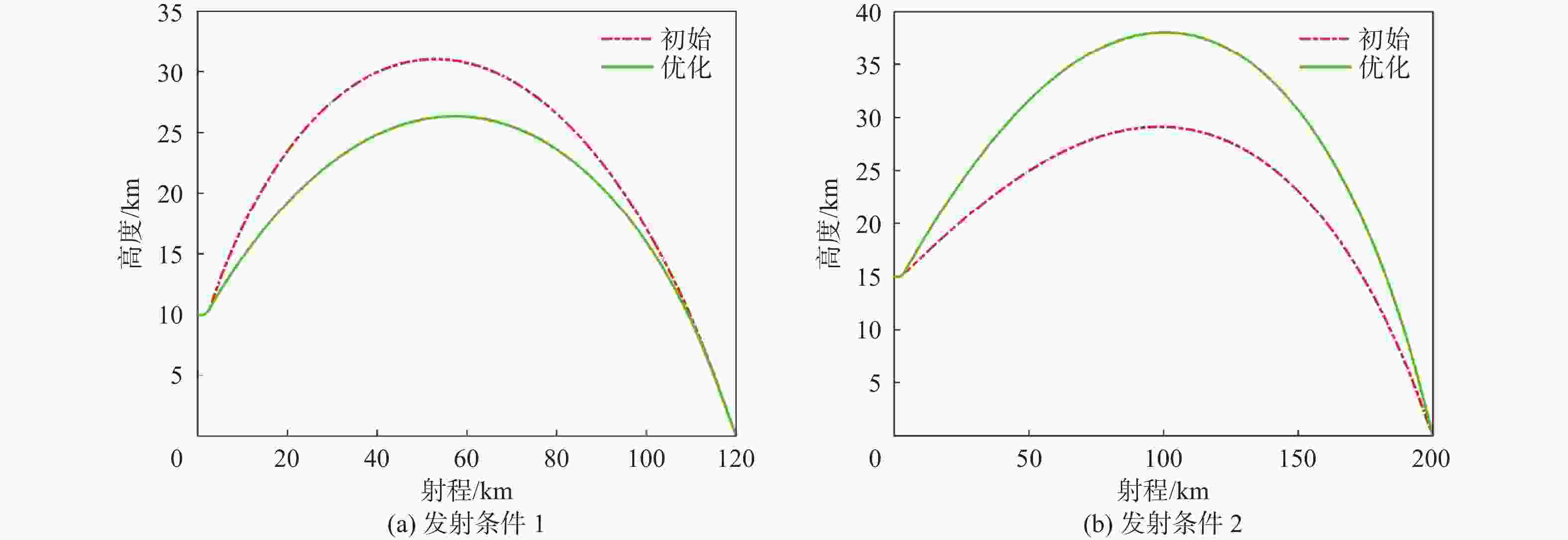
表 1 典型发射条件

Table 1. Typical launch conditions

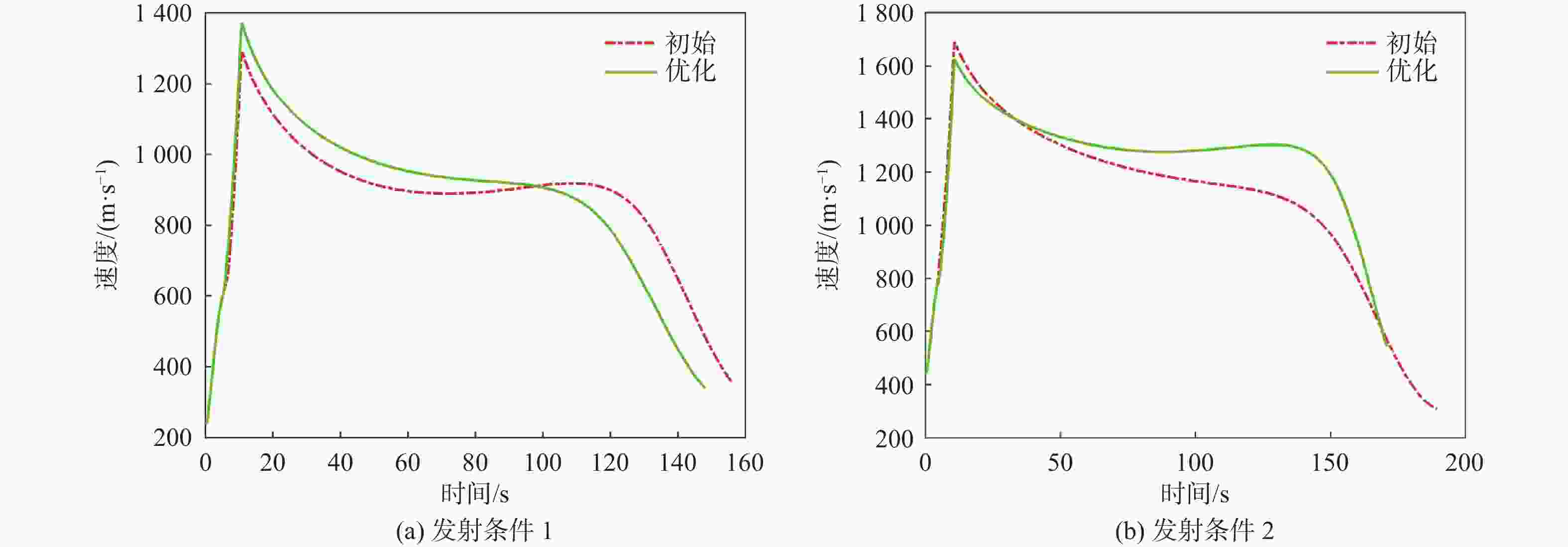
条件	H_m0 /m	Ma_m0	x_t0 /m	y_t0 /m
发射条件 1	10000	0.8	120000	5
发射条件 2	15000	1.5	200000	5

下载: 导出CSV

表 2 优化前后各个阶段的平均速度对比

Table 2. Comparison of average velocity for each stage before and after optimization

条件		平均速度/(m·s^{− 1})
条件		初制导段	中制导段	末制导段
发射条件 1	优化前	440.80	859.68	537.01
发射条件 1	优化后	461.81	922.67	574.77
发射条件 2	优化前	606.81	1175.84	673.88
发射条件 2	优化后	624.51	1254.72	836.02

下载: 导出CSV

表 3 代理模型误差分析

Table 3. Error analysis for surrogate model

发射高度H_m0/km	参数	R²	RMSE
1~5	θ_Δ	0.952	0.095
1~5	θ_f	0.912	0.114
5~10	θ_Δ	0.953	0.101
5~10	θ_f	0.892	0.065
10~15	θ_Δ	0.962	0.058
10~15	θ_f	0.903	0.114
15~20	θ_Δ	0.961	0.066
15~20	θ_f	0.915	0.088

下载: 导出CSV

参考文献(17)

[1]	樊会涛. 空空导弹方案设计原理[M]. 北京: 航空工业出版社, 2013: 67-74. FAN H T. Air-to-air missile conceptual design[M]. Beijing: Aviation Industry Press, 2013: 67-74(in Chinese).
[2]	樊会涛, 崔颢, 天光. 空空导弹70年发展综述[J]. 航空兵器, 2016(1): 3-12. FAN H T, CUI H, TIAN G. A review on the 70-year development of air-to-air missiles[J]. Aero Weaponry, 2016(1): 3-12(in Chinese).
[3]	向开恒, 李人杰, 陈杨. 基于代理模型的空间飞越发射窗口[J]. 北京航空航天大学学报, 2018, 44(12): 2613-2620. XIANG K H, LI R J, CHEN Y. Launch window of space fly-by based on surrogate model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(12): 2613-2620(in Chinese).
[4]	汤祁忠, 李雄, 叶茂, 等. 基于经典遗传算法的末端多约束弹道优化方法[J]. 战术导弹技术, 2019(4): 1-6. TANG Q Z, LI X, YE M, et al. Trajectory optimization method with end-piece multiple constraints based on classical genetic algorithm[J]. Tactical Missile Technology, 2019(4): 1-6(in Chinese).
[5]	李怡昕, 李旭, 刘少波, 等. 高斯伪谱法在变推力导弹弹道优化中的应用[J]. 现代防御技术, 2019, 47(3): 71-77. LI Y X, LI X, LIU S B, et al. Application of gauss pseudo-spectral method in trajectory optimization of variable trust missile[J]. Modern Defence Technology, 2019, 47(3): 71-77(in Chinese).
[6]	李伟喆, 陈万春. 双脉冲中程空空导弹弹道优化[J]. 战术导弹技术, 2018(5): 19-24. LI W Z, CHEN W C. Trajectory optimization of dual-pulse medium range air-to-air missile[J]. Tactical Missile Technology, 2018(5): 19-24(in Chinese).
[7]	韩聪聪, 何华锋, 杨宗浩. 基于单纯形-遗传算法的导弹主动段优化设计[J]. 电光与控制, 2017, 24(10): 22-26. HAN C C, HE H F, YANG Z H. Optimization design of missile active phase based on simplex method and GA[J]. Electronics Optics & Control, 2017, 24(10): 22-26(in Chinese).
[8]	王荣, 张红军, 王贵东, 等. 吸气式空空导弹外形多学科一体化优化设计[J]. 航空学报, 2016, 37(1): 207-215. WANG R, ZHANG H J, WANG G D, et al. Multidisciplinary integrated design optimization for an airbreathing air-to-air missile shape[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 207-215(in Chinese).
[9]	黄诘, 张友安, 刘永新. 一种有撞击角和视场角约束的运动目标的偏置比例导引算法[J]. 宇航学报, 2016, 37(2): 195-202. HUANG J, ZHANG Y A, LIU Y X. A biased proportional guidance algorithm for moving target with impact angle and field-of-view constraints[J]. Journal of Astronautics, 2016, 37(2): 195-202(in Chinese).
[10]	赵曜, 李璞, 刘娟, 等. 带碰撞角约束的三维有限时间滑模制导律[J]. 北京航空航天大学学报, 2018, 44(2): 273-279. ZHAO Y, LI P, LIU J, et al. Finite-time sliding mode control based 3D guidance law with impact angle constraints[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 273-279(in Chinese).
[11]	杨雪榕, 梁加红, 李晓冬. 空空导弹高抛弹道仿真研究[J]. 系统仿真学报, 2010, 22(5): 1261-1265. YANG X R, LIANG J H, LI X D. Study on parabola-trajectory simulation of air-to-air missile[J]. Journal of System Simulation, 2010, 22(5): 1261-1265(in Chinese).
[12]	陈韵, 常燕, 苗昊春, 等. 落角约束最优制导律在空地导弹上的应用[J]. 弹箭与制导学报, 2018, 38(5): 141-144. CHEN Y, CHANG Y, MIAO H C, et al. Optimal guidance law with terminal angular constraint use in air-to-ground missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2018, 38(5): 141-144(in Chinese).
[13]	ERER K S, TEKIN R. Impact time and angle control based on constrained optimal solutions[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(10): 1-7.
[14]	史绍琨, 赵久奋, 崇阳, 等. 带落角约束的新型二阶滑模三维制导律[J]. 北京航空航天大学学报, 2019, 45(3): 614-623. SHI S K, ZHAO J F, CHONG Y, et al. Novel second-order sliding mode control based 3D guidance law with impact angle constraints[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(3): 614-623(in Chinese).
[15]	魏黎明, 李晓龙, 赵征, 等. 神经网络在吸气式高超声速导弹突防弹道设计上的应用[J]. 空天防御, 2018, 1(2): 14-17. WEI L M, LI X L, ZHAO Z, et al. Application of neural network in penetration of air-breathing hypersonic missile[J]. Air & Space Defense, 2018, 1(2): 14-17(in Chinese).
[16]	赵山杉, 张雯, 李晶, 等. 基于多岛遗传算法的小型有效载荷分离装置质量优化设计[J]. 导弹与航天运载技术, 2017(2): 16-19. ZHAO S S, ZHANG W, LI J, et al. Mass optimization design of separation devices for pint-size load based on multi-island genetic algorithm[J]. Missiles and Space Vehicles, 2017(2): 16-19(in Chinese).
[17]	张鼎逆, 刘毅. 基于改进遗传算法和序列二次规划的再入轨迹优化[J]. 浙江大学学报(工学版), 2014, 48(1): 161-167. ZHANG D N, LIU Y. Reentry trajectory optimization based on improved genetic algorithm and sequential quadratic programming[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(1): 161-167(in Chinese).