-
摘要:
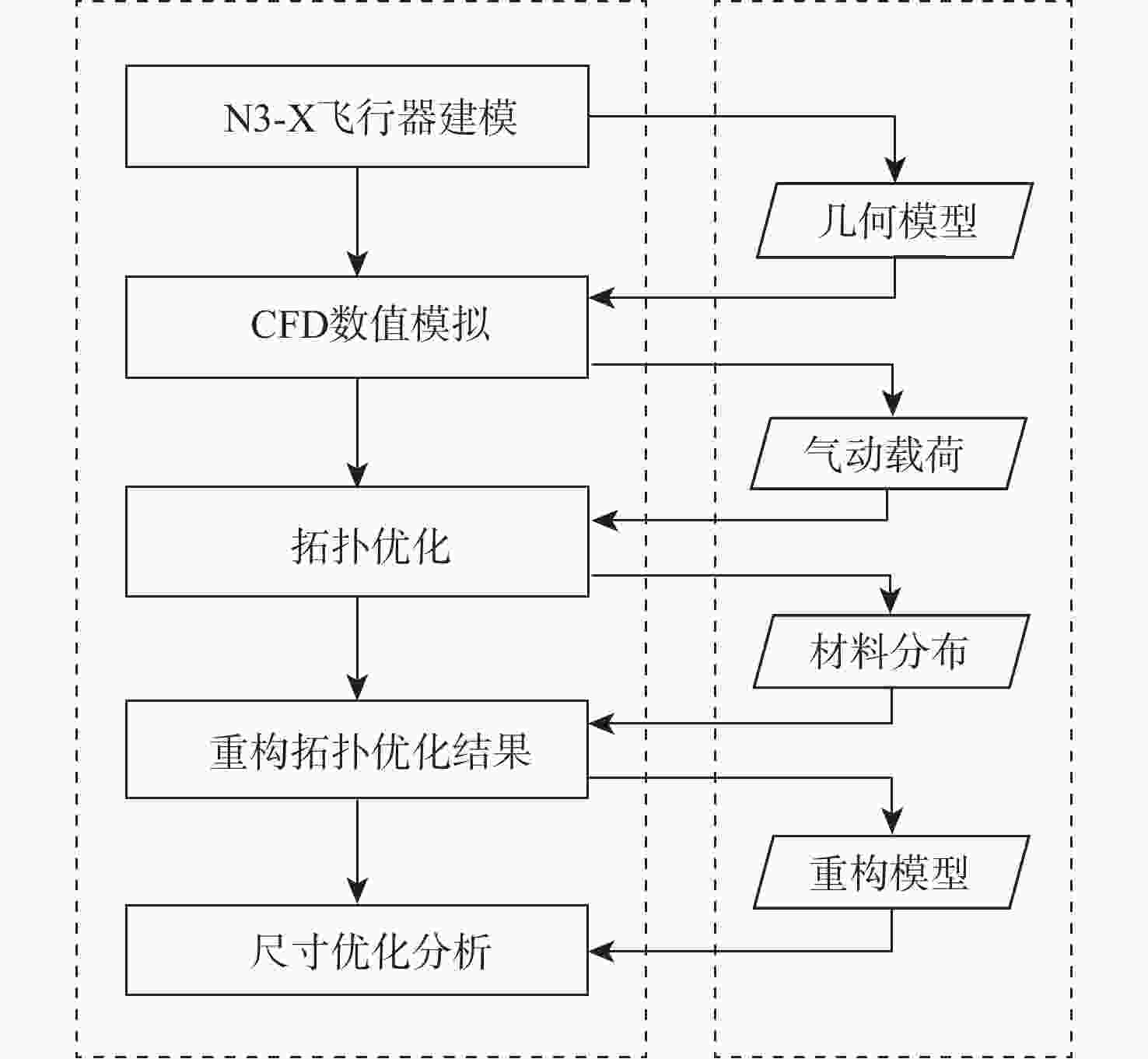
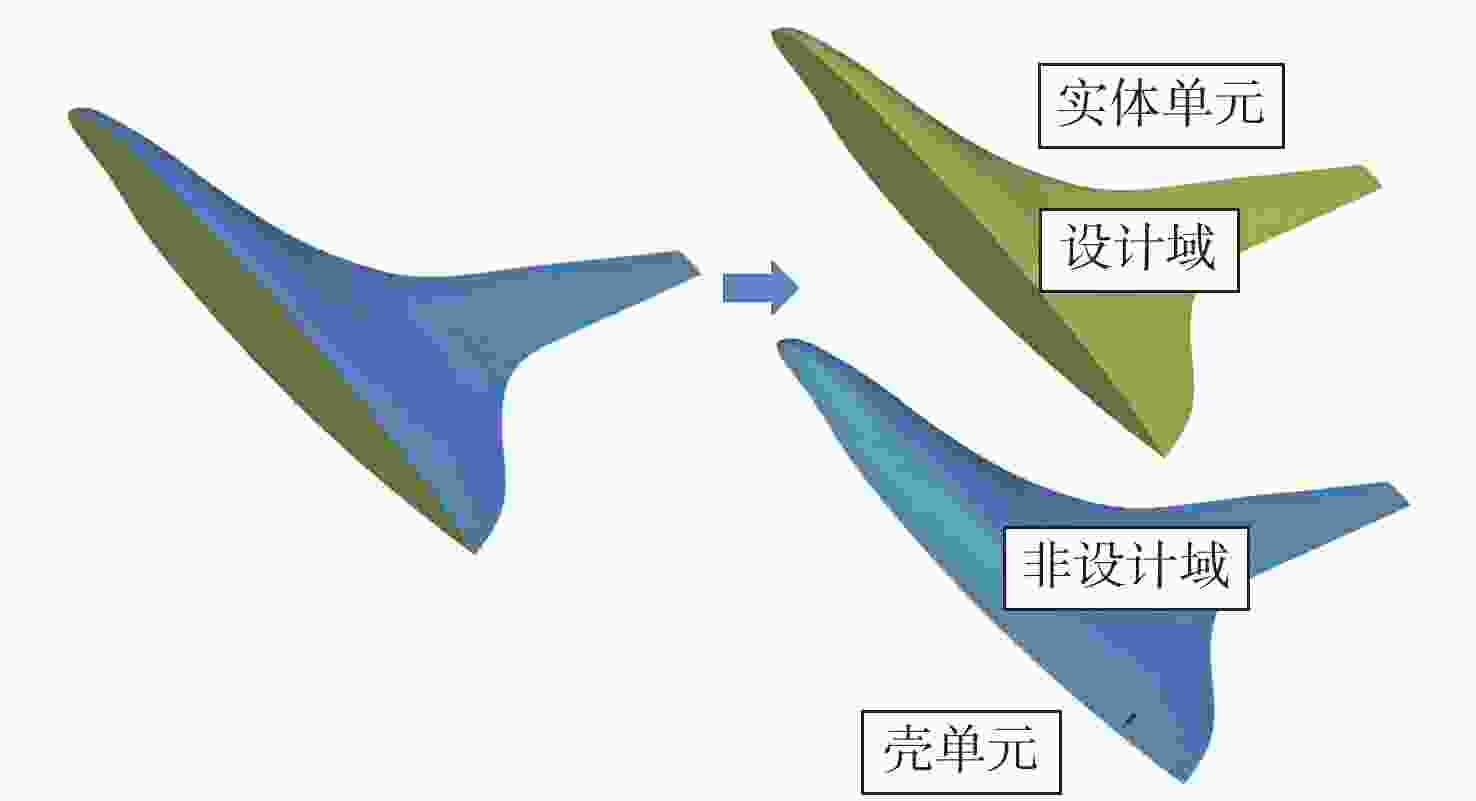
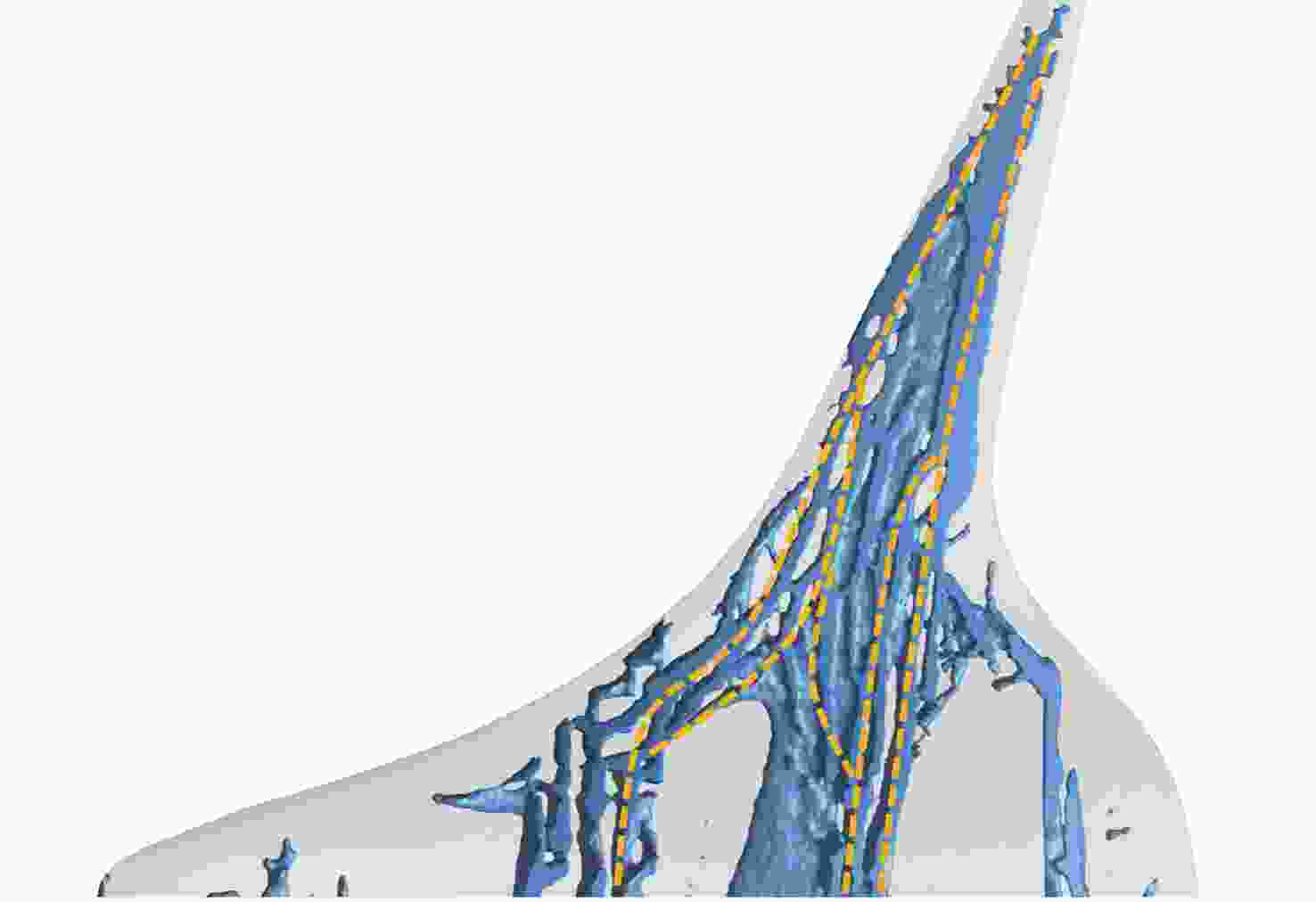
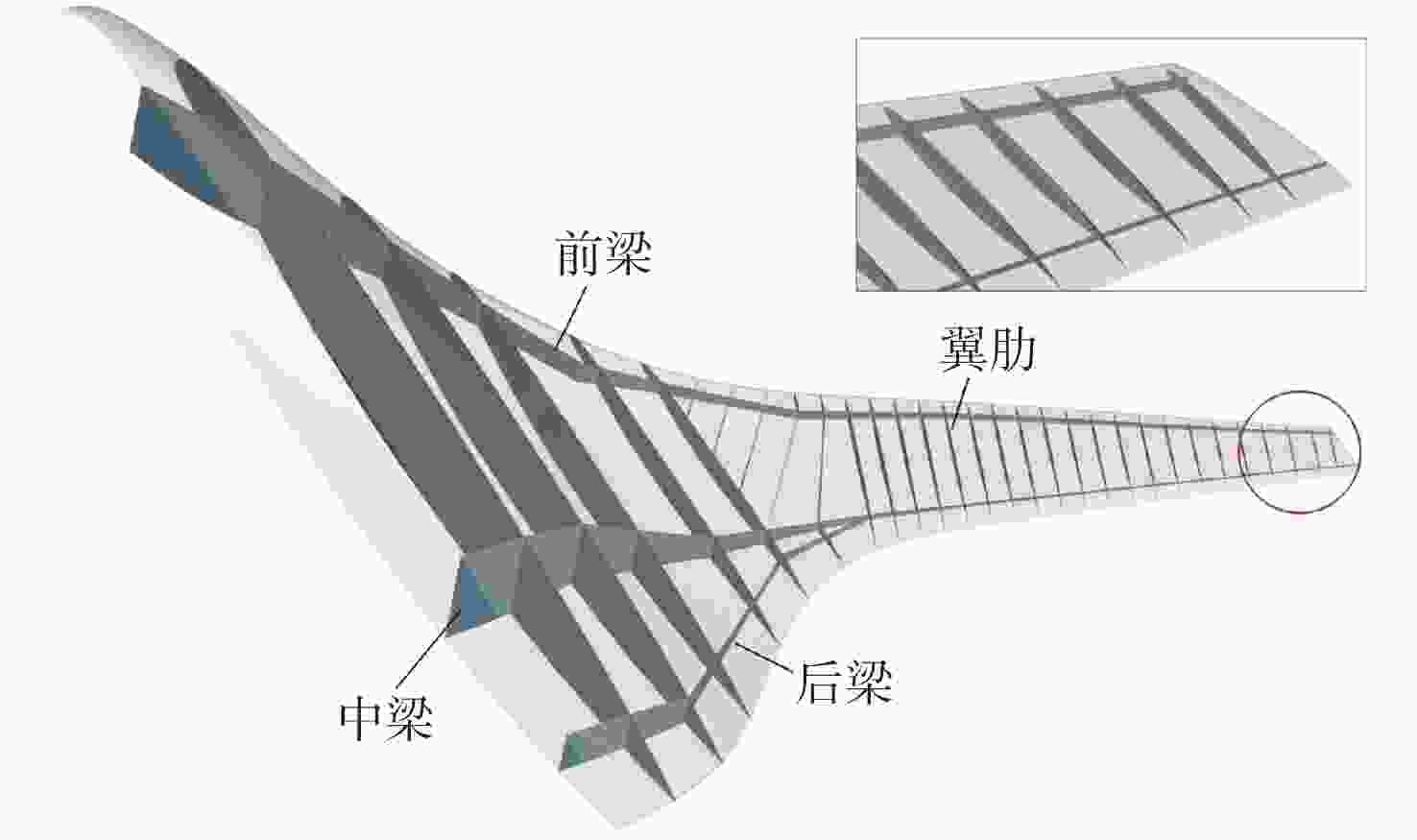
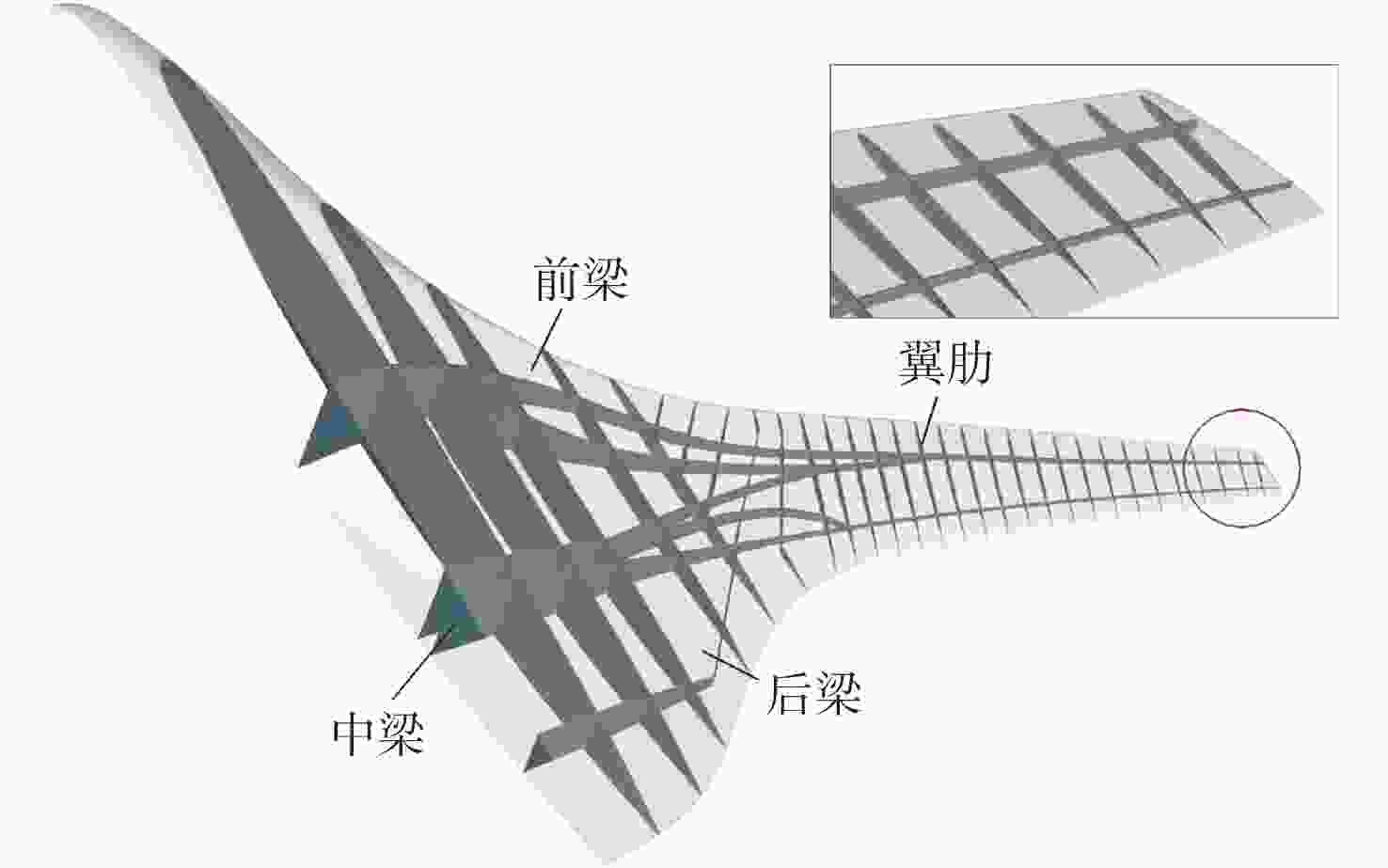
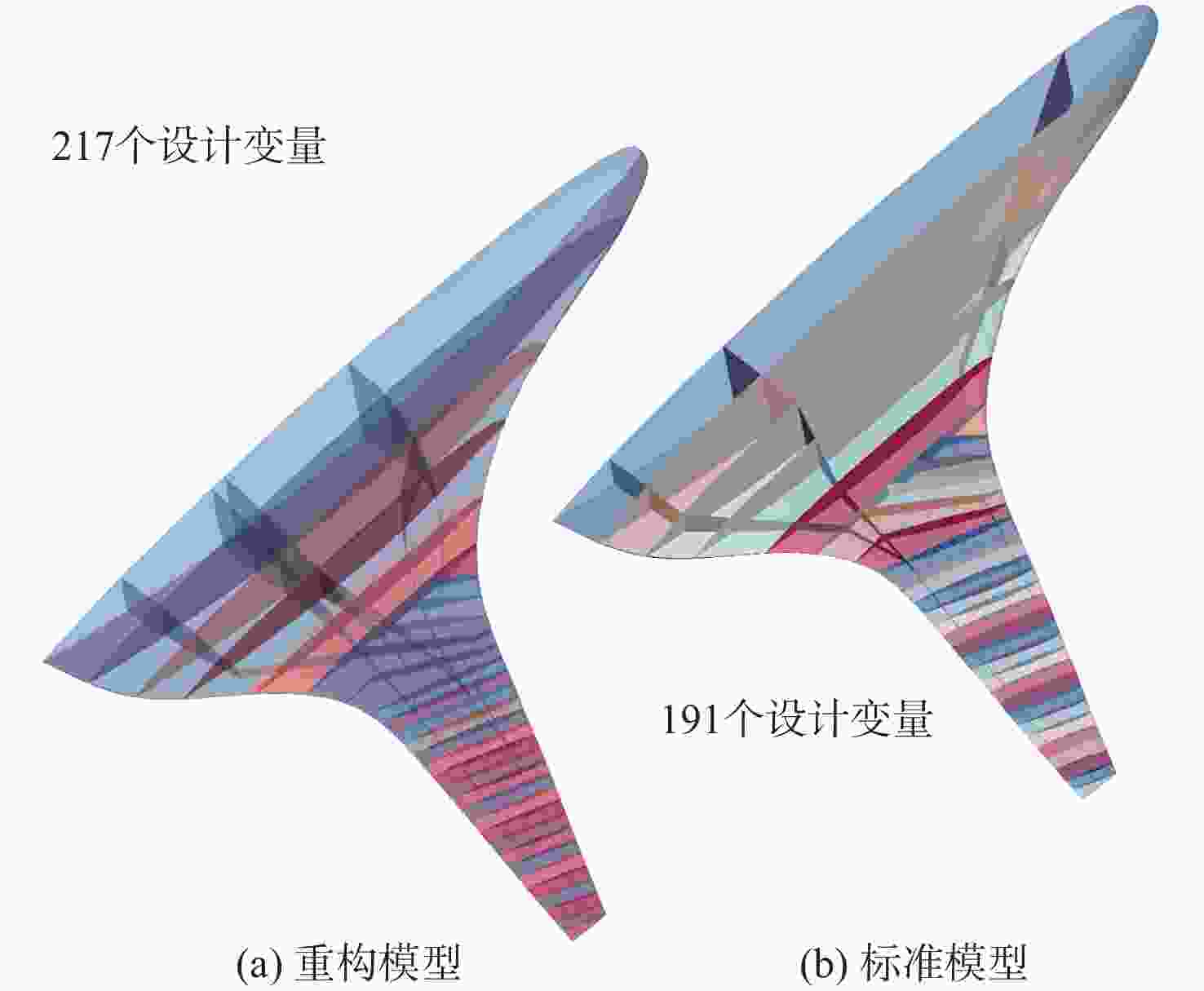
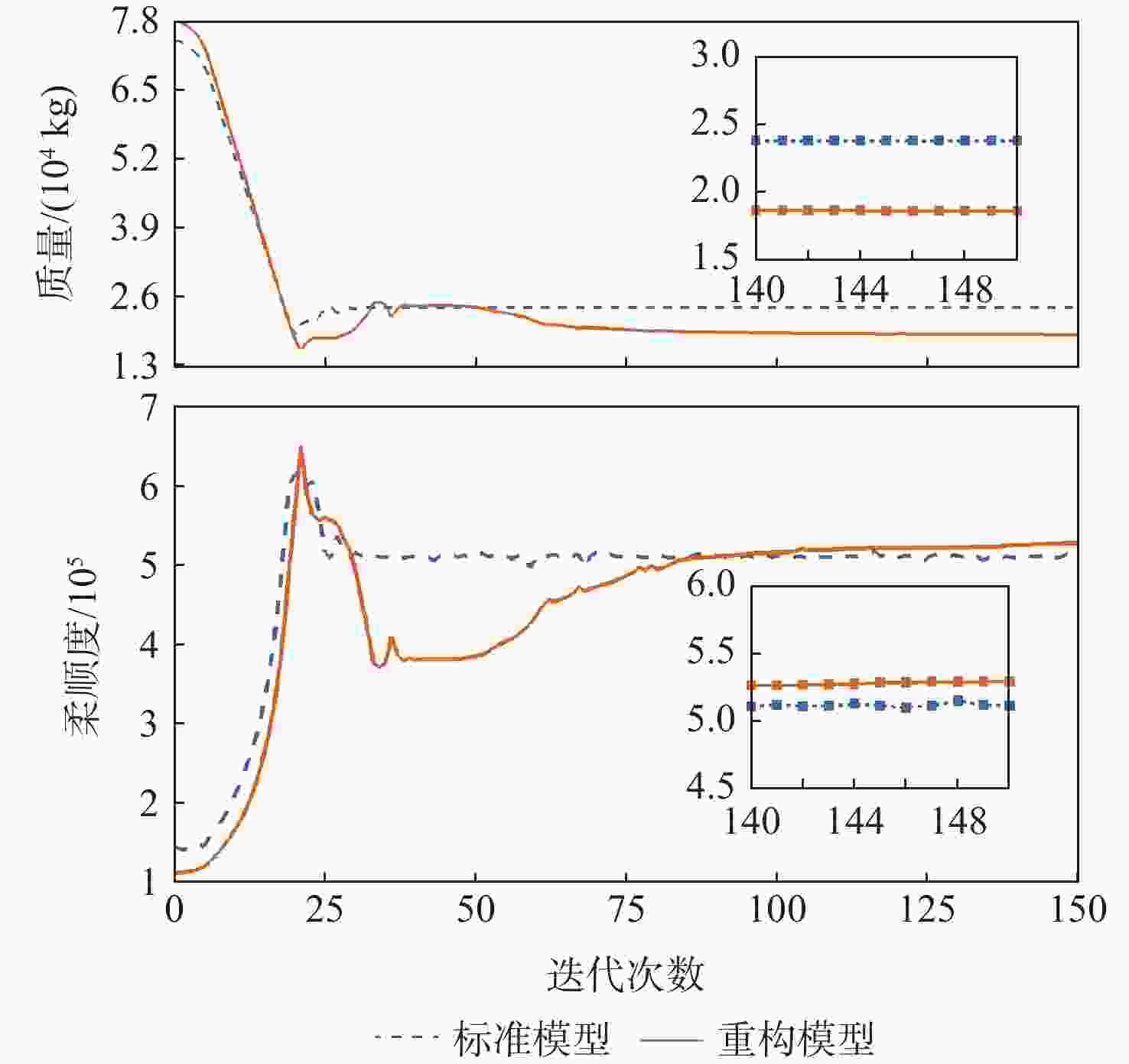
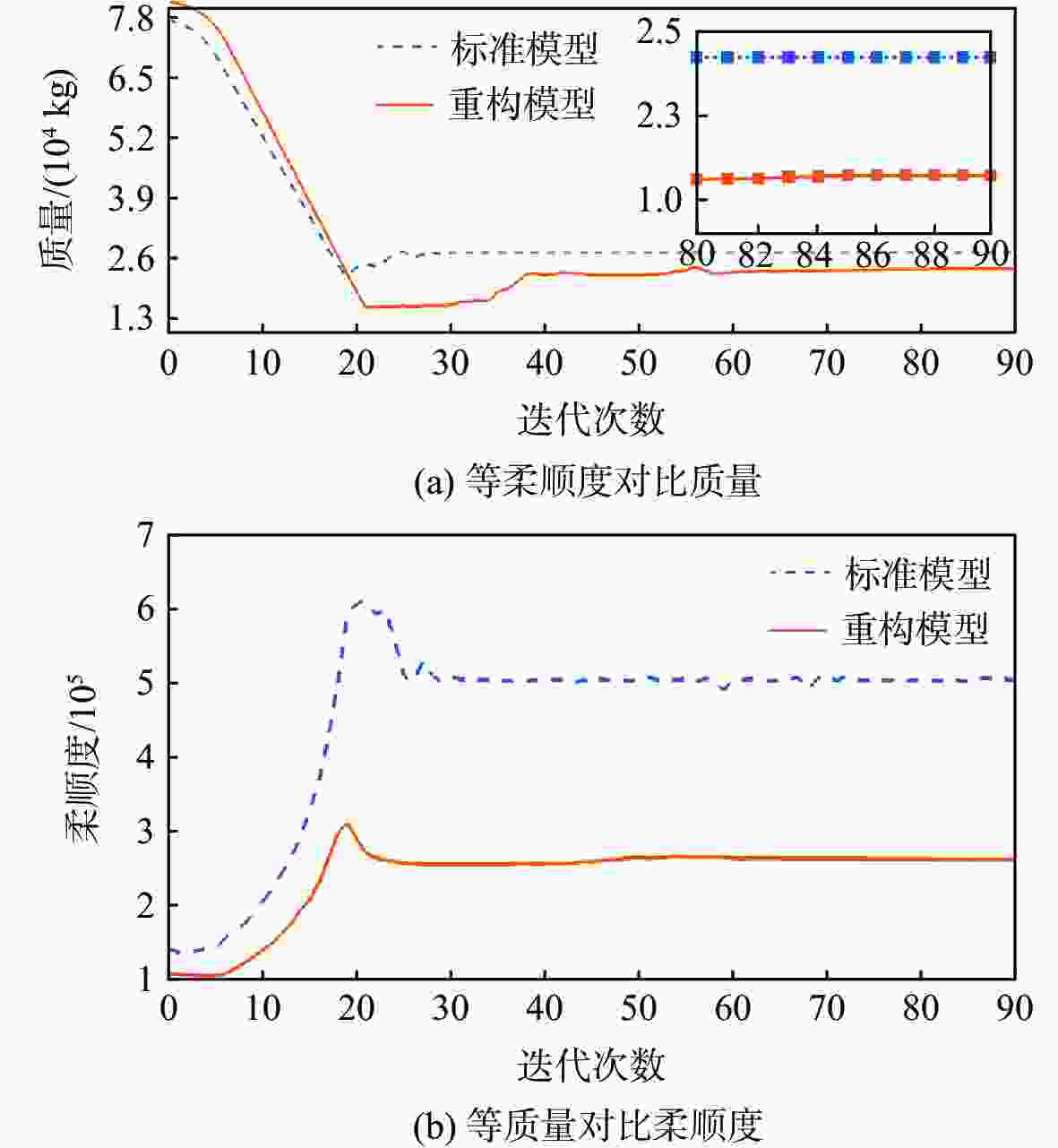
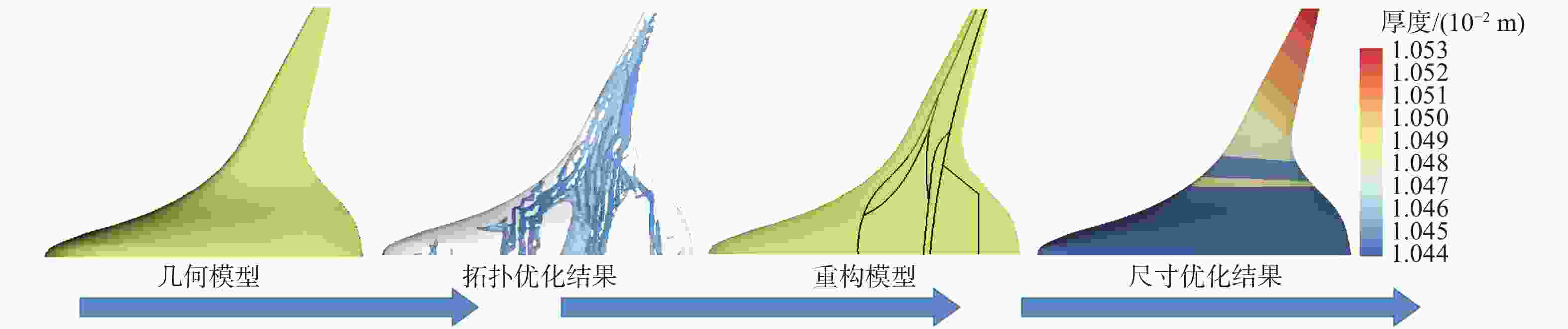
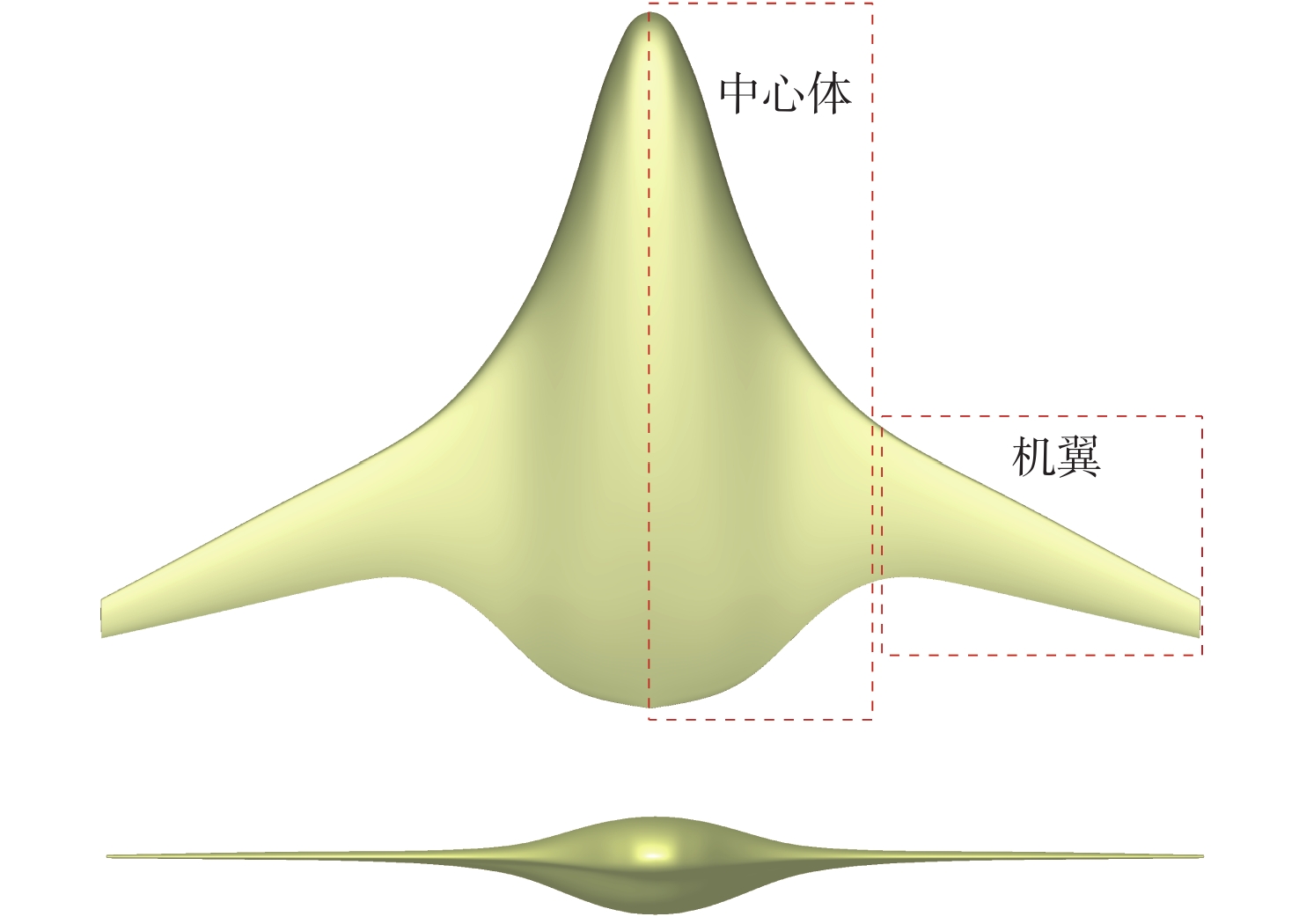
飞翼布局飞行器由于具有气动效率高的优势，将成为未来航空飞行器发展的主流方向，然而结构质量限制了其性能的进一步提升，结构优化是实现结构减重的重要技术。以飞翼布局飞行器内部结构为研究对象，建立拓扑优化模型，以柔顺度作为目标函数，探究飞翼布局飞行器全机内部结构的最优布置方式，分析弯曲梁构件在飞翼布局飞行器结构优化中的作用和减重机制，根据拓扑优化结果建立重构模型，同时依据Boeing第二代结构设计建立标准模型，使用尺寸优化评估重构模型相较于标准模型的减重效果。结果表明：在等柔顺度时，重构模型相比标准模型质量减少14.53%；在等质量时，重构模型相比标准模型全机柔顺度降低47.90%，并减少了44.87%的
z 向最大位移，拓扑优化减重和增加刚度效果显著，验证了弯曲梁构件的减重作用。研究结果可为飞翼布局飞行器结构减重优化奠定基础，建立的优化评估机制可为飞翼布局飞行器的内部结构设计提供参考。Abstract:Flying wing aircraft will become the mainstream of future aircraft due to its high aerodynamic efficiency; however, its performance improvement is limited by structural weight. Structural optimization is an important technique to reduce structural weight. A topology optimization model is thus established based on the internal structure of flying wing aircraft with the compliance of the aircraft skin as the objective function. The optimal arrangement of this structure is studied, and the effect and weight reduction mechanism of curvilinear spars are investigated in the structural optimization of the aircraft. The rebuilt model and the standard model are developed according to the topology optimization results and the Boeing second generation structure design respectively, using sizing optimization to evaluate the effect of topology optimization. Results show that compared with the standard model, the rebuilt model decreases the mass by 14.53% with the same compliance. The compliance of the reconstructed model is decreased by 47.90% and the maximum
z -displacement is reduced by 44.87% with the same quality, showing significant decrease in weight reduction and increase in stiffness for topology optimization. The weight reduction effect of curvilinear spars is also validated. The results of this study can lay a foundation for weight reduction optimization of flying wing aircraft, and the optimization-evaluation mechanism can provide insight into the internal structural design of flying wing aircraft.-
Key words:
- flying wing aircraft /
- topology optimization /
- sizing optimization /
- curvilinear spar /
- weight reduction
-
图 6 机体柔顺度为优化目标的拓扑优化迭代历程
Figure 6. Iteration history with body compliance as optimization object
图 7 蒙皮柔顺度为优化目标的拓扑优化迭代历程
Figure 7. Iteration history with skin compliance as optimization object
图 12 重构模型和标准模型的有限元模型
Figure 12. Finite element model of rebuilt model and standard model
图 13 标准模型和重构模型的设计变量分布
Figure 13. Distribution of design variables of standard model and rebuilt model
图 14 标准模型和重构模型的尺寸优化迭代过程
Figure 14. Iteration history of sizing optimization for standard model and rebuilt model
图 15 质量约束和柔顺度约束的尺寸优化结果
Figure 15. Sizing optimization with mass and compliance constraint
表 2 优化结果
Table 2. Optimization results
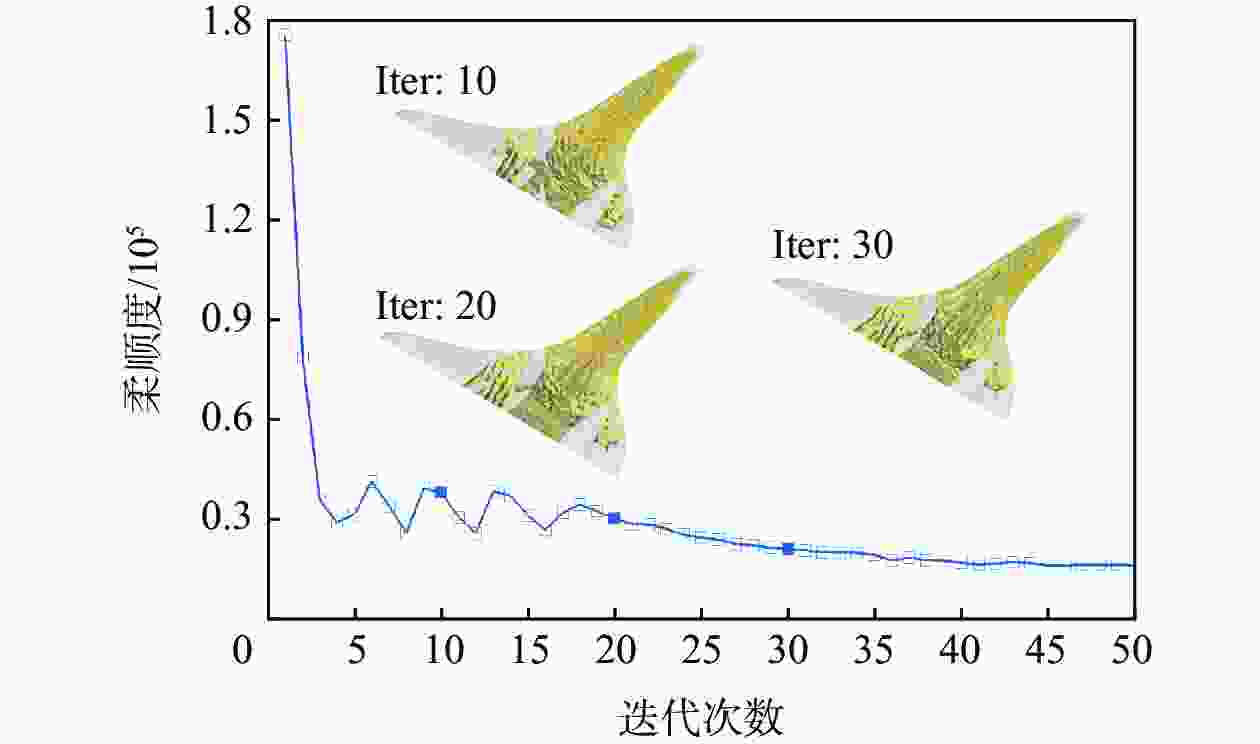
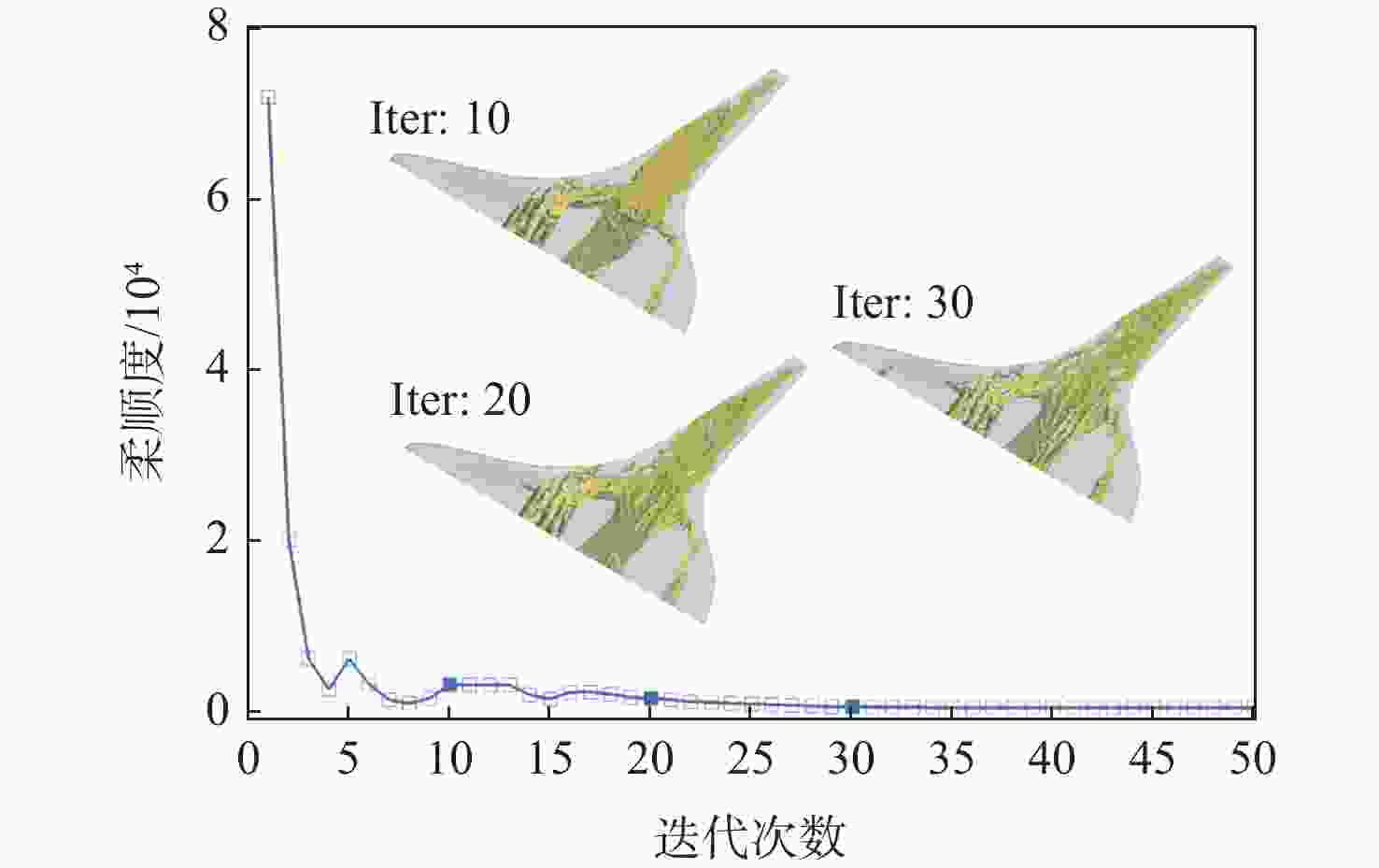
模型 质量/kg 柔顺度 标准构型 23782 513250 重构模型1 23782 267406
（47.90%↓）重构模型2 20327
（14.53%↓）513250 
下载: 导出CSV
-
[1] 孔祥浩, 张卓然, 陆嘉伟, 等. 分布式电推进飞机电力系统研究综述[J]. 航空学报, 2018, 39(1): 51-67.KONG X H, ZHANG Z R, LU J W, et al. Review of electric power system of distributed electric propulsion aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 51-67(in Chinese). [2] 黄俊. 分布式电推进飞机设计技术综述[J]. 航空学报, 2021, 42(3): 624037.HUANG J. Survey on design technology of distributed electric propulsion aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 624037(in Chinese). [3] FELDER J, TONG M, CHU J. Sensitivity of mission energy consumption to turboelectric distributed propulsion design assumptions on the N3-X hybrid wing body aircraft[C]//48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston: AIAA, 2012: 3701. [4] ARMSTRONG M J, ROSS C A H, BLACKWELDER M J, et al. Trade studies for NASA N3-X turboelectric distributed propulsion system electrical power system architecture[J]. SAE International Journal of Aerospace, 2012, 5(2): 325-336. doi: 10.4271/2012-01-2163 [5] VOGEL A, JUNKER P. Adaptive thermodynamic topology optimization[J]. Structural and Multidisciplinary Optimization, 2021, 63(1): 95-119. doi: 10.1007/s00158-020-02667-4 [6] ESCHENAUER H A, OLHOFF N. Topology optimization of continuum structures: A review[J]. Applied Mechanics Reviews, 2001, 54(4): 331-390. [7] KROG L, TUCKER A, KEMP M, et al. Topology optimisation of aircraft wing box ribs[C]//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2004: 4481. [8] SONG L L, GAO T, TANG L, et al. An all-movable rudder designed by thermo-elastic topology optimization and manufactured by additive manufacturing[J]. Computers & Structures, 2021, 243(5): 35-47. [9] MAUTE K, ALLEN M. Conceptual design of aeroelastic structures by topology optimization[J]. Structural and Multidisciplinary Optimization, 2004, 27(1): 27-42. [10] AAGE N, ANDREASSEN E, LAZAROV B, et al. Giga-voxel computational morphogenesis for structural design[J]. Nature, 2017, 550(7674): 84-86. [11] LOCATELLI D, MULANI S B, KAPANIA R K. Wing-box weight optimization using curvilinear spars and ribs (SpaRibs)[J]. Journal of Aircraft, 2011, 48(5): 1671-1684. [12] ZHU J H, ZHANG W H, XIA L. Topology optimization in aircraft and aerospace structures design[J]. Archives of Computational Methods in Engineering, 2016, 23(4): 595-622. doi: 10.1007/s11831-015-9151-2 [13] LIOU M F, KIM H, LEE B, et al. Aerodynamic design of integrated propulsion–Airframe configuration of a hybrid wing body aircraft[J]. Shock Waves, 2019, 29(8): 1043-1064. doi: 10.1007/s00193-019-00933-z [14] GOLDBERG C, NALIANDA D, PILIDIS P, et al. Economic viability assessment of NASA’s blended wing body N3-X aircraft[C]//53rd AIAA/SAE/ASEE Joint Propulsion Conference. Reston: AIAA, 2017: 4604. [15] ROZVANY G I N, ZHOU M, BIRKER T. Generalized shape optimization without homogenization[J]. Structural Optimization, 1992, 4(3-4): 250-252. doi: 10.1007/BF01742754 [16] BENDSØE M, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69: 635-654. doi: 10.1007/s004190050248 [17] BARCLAY A. SQP methods for large-scale optimization[D]. San Diego: University of California, 1999: 76-78. [18] KIM H, LIOU M F. Flow simulation and drag decomposition study of N3-X hybrid wing-body configuration[J]. Aerospace Science & Technology, 2019, 85(2): 24-39. [19] ROBINSON J H, DOYLE S, OGAWA G, et al. Aeroservoelastic optimization of wing structure using curvilinear spars and ribs (SpaRibs)[C]//17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2016: 3994. [20] JUTTE C V, STANFORD B K, WIESEMAN C D. Internal structural design of the common research model wing box for aeroelastic tailoring[R]. Washington, D. C. : NASA, 2015: 23-39. [21] JEGLEY D C, PRZEKOP A, LOVEJOY A E, et al. Structural response of a stitched composite hybrid wing body center section[J]. Journal of Aircraft, 2021, 58(3): 580-590. doi: 10.2514/1.C035911 [22] LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft, 2004, 41(1): 10-25. doi: 10.2514/1.9084 [23] KENNEDY G J, MARTINS J R R A. A parallel finite-element framework for large-scale gradient-based design optimization of high-performance structures[J]. Finite Elements in Analysis and Design, 2014, 87(9): 56-73. -
下载:
点击查看大图
计量
- 文章访问数: 749
- HTML全文浏览量: 109
- PDF下载量: 118
- 被引次数: 0
