-
摘要:
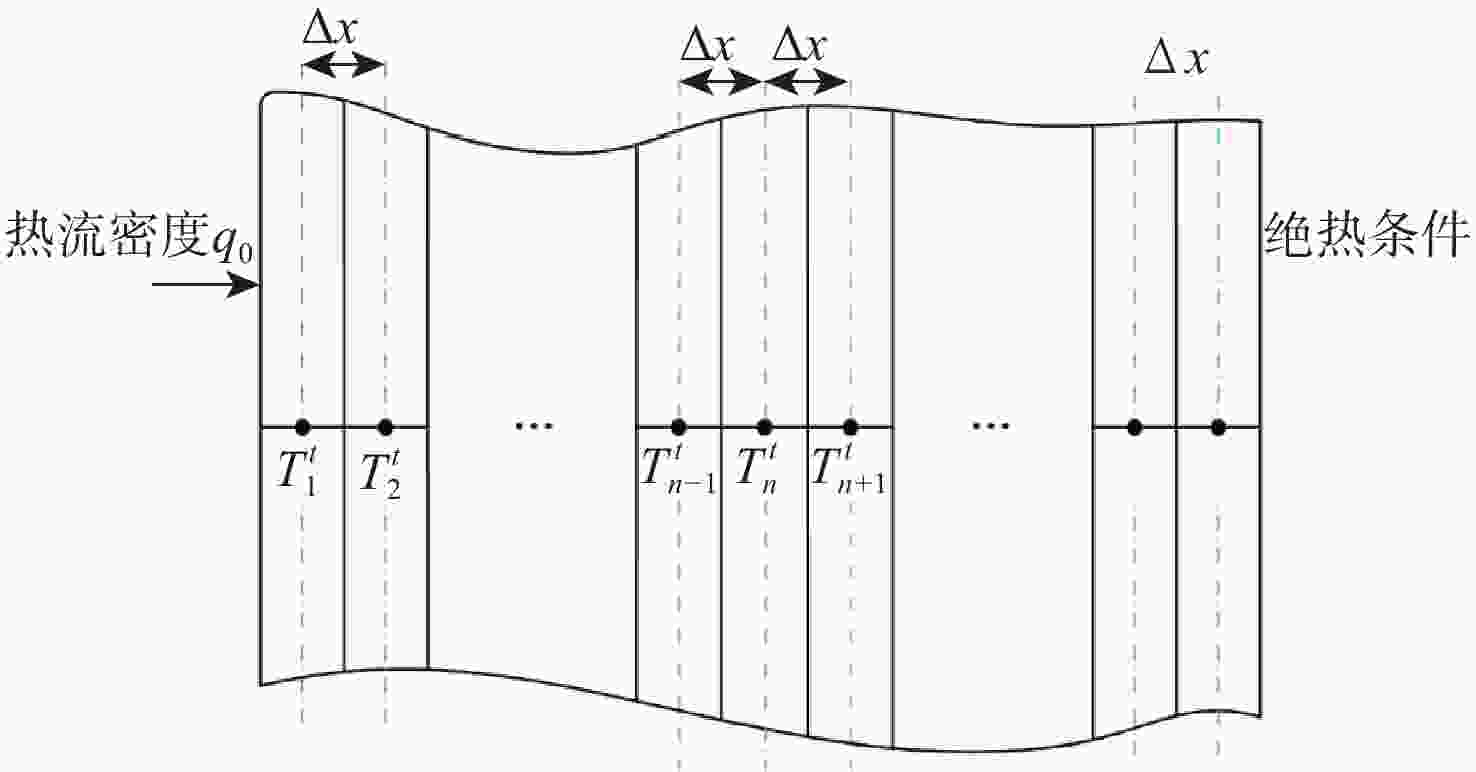
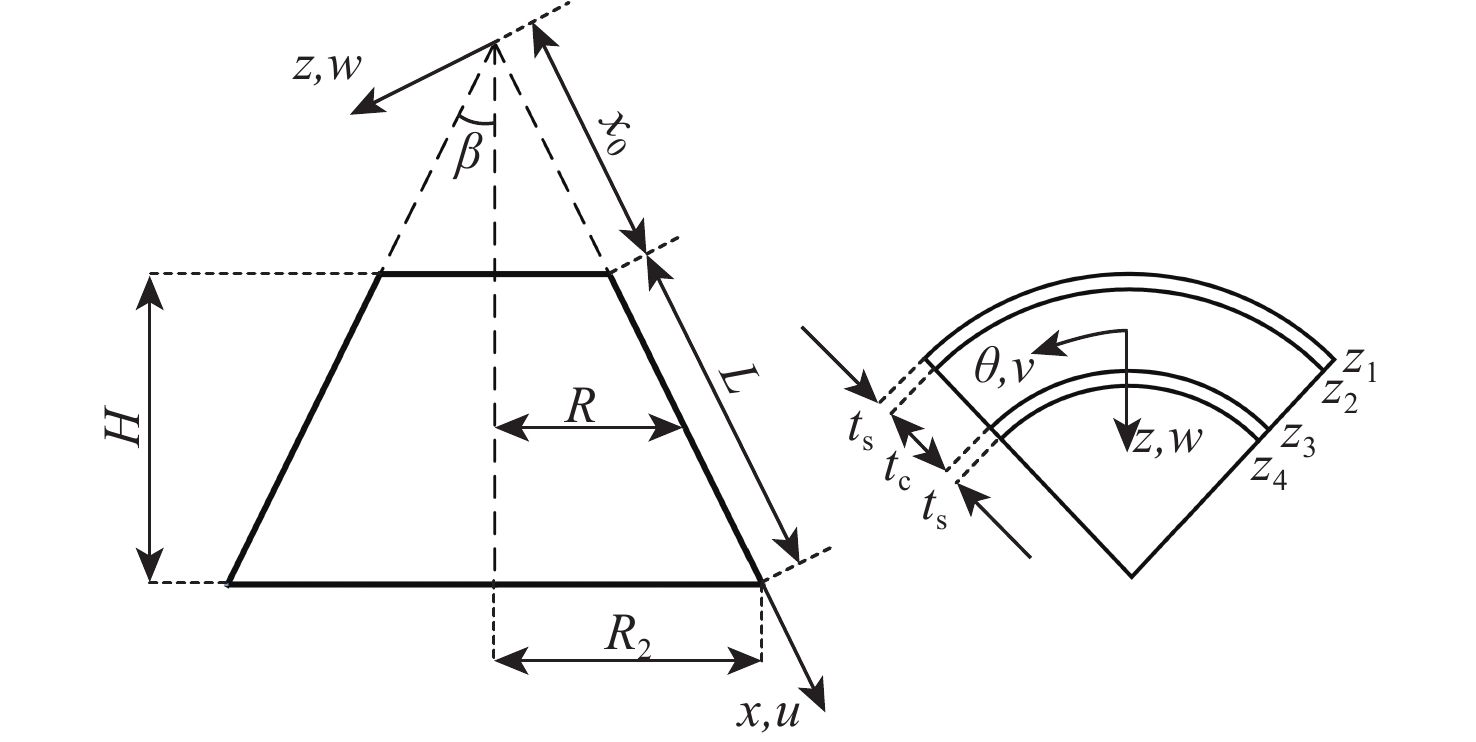
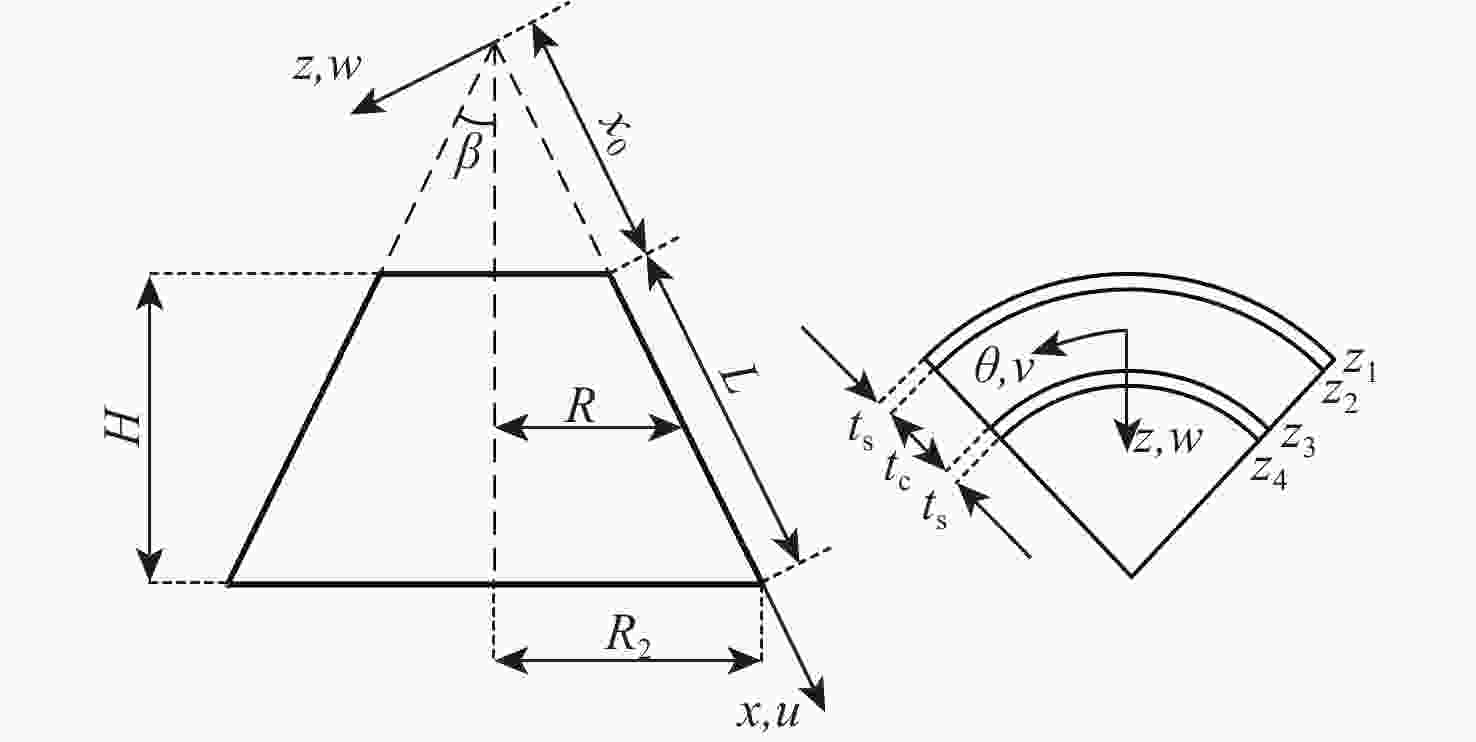
为分析运载火箭整流罩锥壳夹层结构不确定性对结构热稳定性的影响并指导结构的轻量化设计，建立整流罩前锥段夹层圆锥壳模型，并建立温度场模型，据此对圆锥壳开展热稳定性分析，推导力热联合载荷作用下整流罩前锥段夹层结构失稳临界轴压。在此基础上，针对主要不确定性因素，开展灵敏度分析并建立区间不确定性优化模型，采用区间可能度方法将其转化为确定性问题，并采用遗传算法-区间分析算法（GA-CIAM）实现结构优化设计。计算结果表明：考虑气动力/热载荷及材料参数不确定性影响，对整流罩前锥段结构开展优化设计，在满足设计要求的前提下，有效实现结构轻量化。
Abstract:In order to analyze the influence of uncertainty on the thermal stability of the launch vehicle fairing cone shell sandwich structure and to guide the lightweight design of the structure, a model of the fairing front cone section sandwich shell is established and a temperature field model is built, based on which the thermal stability analysis of the cone shell is carried out and the critical axial pressure under the combined force-thermal load is derived. For the primary uncertainty factors, interval uncertainty optimization models and sensitivity analyses are also produced. The interval probability approach is then used to convert these models into deterministic optimization problems, which are then resolved using the genetic algorithm-collocation interval analysis method (GA-CIAM) method. The calculation results show that considering the influence of aerodynamic/thermal load and material parameter uncertainty, the optimization design of the front cone section of the fairing can effectively realize the structural lightweight on the premise of meeting the design requirements.
-
图 1 前锥段夹层结构参数化模型
Figure 1. Parameterized model of sandwich structure of the front cone section
表 1 设计变量设计空间及初值
Table 1. Design space and initial value of design variables
参数 面板厚度${t_{\rm{s}}}/{\text{mm} }$ 芯子厚度${t_{\rm{c}}}/{\text{mm} }$ 设计空间 $\left[ {0.5 ,3} \right]$ $\left[ {2,50 } \right]$ 初始值 1.5 18 
下载: 导出CSV
表 2 不确定性变量上下界
Table 2. upper and lower bounds of uncertainty variables
不确定性变量 变量上下界 需用轴压载荷$F$/MN [14.25,15.75] 净吸收热流${q_0}$/（kW·m−2) [19,21] 热流作用时间$t$/s [142.5,157.5] 玻璃板弹性模量${E_{\rm{s}}}$/MPa [68400,75600] 泡沫夹层弹性模量${E_{\rm{c}}}$/MPa [66.5,73.5] 玻璃板比热容${c_{\rm{s}}}$/（kJ·(kg·K)−1） [1.425,1.575] 泡沫夹层比热容${c_{\rm{c}}}$/（kJ·(kg·K)−1） [1.188,1.313] 玻璃板导热率${k_{\rm{s}}}$/（kW·(m·K)−1） [3.04×10−4,
3.36×10−4]泡沫夹层导热率${k_{\rm{c}}}$/（kW·(m·K)−1） [2.85×10−5,
3.15×10−5]
下载: 导出CSV
表 3 优化结果对比
Table 3. Comparison of optimization results
优化 设计变量/mm 结构质量/kg 临界轴压/MN 内壁温度/℃ 外壁温度/℃ 优化前 [2/18] 414.206 [21.676,24.826] [20.002,20.003] [572.055,611.647] 优化后 [1.600/16.500] 352.674 [14.230,18.087] [20.002,20.019] [603.321,769.212]
下载: 导出CSV
表 4 不同可能度水平下不确定性优化结果
Table 4. Uncertainty optimization results under different possibility levels
可能度
水平$\lambda $最优设计变量$\left[ { {t_{\rm{s} } },{t_{\rm{c} } } } \right]/{\text{mm} }$ 优化后目标
函数值$M/{\text{kg}}$0.2 [1.520/15.759] 335.288 0.5 [1.387/18.314] 344.726 0.8 [1.600/16.500] 352.674 1.0 [1.765/15.765] 364.333
下载: 导出CSV
-
[1] 杨灿. 耐高温复合材料整流罩性能及热力学分析 [D]. 哈尔滨: 哈尔滨工程大学, 2014.YANG C. Study on the high temperature-resistant composites fairing and its mechanical properities under high service temperature [D]. Harbin: Harbin Engineering University, 2014(in Chinese). [2] MEYERS C A, HYER M W, SHUART M J. Thermal buckling and postbuckling of symmetrically laminated composite plates[J]. Journal of Thermal Stresses, 1992, 14(4): 519-540. [3] NAJ R, BOROUJERDY M S, ESLAMI M R. Thermal and mechanical instability of functionally graded truncated conical shells[J]. Thin-Walled Structures, 2008, 46(1): 65-78. doi: 10.1016/j.tws.2007.07.011 [4] DUNG D V, CHAN D Q. Analytical investigation on mechanical buckling of FGM truncated conical shells reinforced by orthogonal stiffeners based on FSDT[J]. Composite Structures, 2017, 159(1): 827-841. [5] DUC N D, SEUNG-EOCK K, CHAN D Q. Thermal buckling analysis of FGM sandwich truncated conical shells reinforced by FGM stiffeners resting on elastic foundations using FSDT[J]. Journal of Thermal Stresses, 2017, 41(3): 1-35. [6] TORABI J, KIANI Y, ESLAMI M R. Linear thermal buckling analysis of truncated hybrid FGM conical shells[J]. Composites Part B Engineering, 2013, 50(7): 265-72. [7] 张东, 穆京京, 蒋亦幪, 等. 轴压下圆柱加筋壳的热屈曲[J]. 强度与环境, 2019, 46(6): 32-37. doi: 10.19447/j.cnki.11-1773/v.2019.06.005ZHANG D, MU J J, JIANG Y M, et al. Thermal buckling of stiffened cylinders under axial compression[J]. Structure & Environment Engineering, 2019, 46(6): 32-37(in Chinese). doi: 10.19447/j.cnki.11-1773/v.2019.06.005 [8] 唐统帅. 基于散热和承载功能的格栅加筋板研究 [D]. 哈尔滨: 哈尔滨工业大学, 2014.TANG T S. Research on grid-stiffened panels base on heat transfer and load-carrying capacity [D]. Harbin: Harbin Institute of Technology, 2014(in Chinese). [9] 徐腾飞, 辛健强, 董永朋, 等. 柔性支撑上FGM矩形薄板热屈曲的封闭形式解[J]. 强度与环境, 2018, 45(3): 20-29. doi: 10.19447/j.cnki.11-1773/v.2018.03.004XU T F, XIN J Q, DONG Y P, et al. Closed form solution for thermal buckling of rectangular FGM thin plates with flexible support[J]. Structure & Environment Engineering, 2018, 45(3): 20-29(in Chinese). doi: 10.19447/j.cnki.11-1773/v.2018.03.004 [10] BELLMAN R E, ZADEH L A. Application series decision-making in a fuzzy environment[J]. Management Science, 1970, 17(4): 141-164. doi: 10.1287/mnsc.17.4.B141 [11] FAES M. Interval methods for the identification and quantification of inhomogeneous uncertainty in finite element models [D]. Belgium: KU Leuven, 2017. [12] 尹莲花. 高速飞行器热防护结构分析与热结构优化方法研究 [D]. 北京: 北京理工大学, 2008.YIN L H. Analysis of thermal protection structure and study of thermal structural optimization for high speed aircraft [D]. Beijing: Beijing Institute of Technology, 2008(in Chinese). [13] BRUSH D O, ALMROTH B O, HUTCHINSON J W. Buckling of bars, plates, and shells[J]. Journal of Applied Mechanics, 1975, 42(4): 911. [14] JIANG C, HAN X, LIU G R, et al. A nonlinear interval number programming method for uncertain optimization problems[J]. European Journal of Operational Research, 2008, 188(1): 1-13. doi: 10.1016/j.ejor.2007.03.031 [15] 祁武超, 邱志平. 基于区间分析的结构非概率可靠性优化设计[J]. 中国科学:物理学 力学 天文学, 2013, 43(1): 85-93.QI W C, QIU Z P. Non-probabilistic reliability-based structural design optimization based on the interval analysis method[J]. Science China Physics, Mechanics & Astronomy, 2013, 43(1): 85-93(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 446
- HTML全文浏览量: 121
- PDF下载量: 19
- 被引次数: 0
